Васильев Иван Анатольевич
Санкт-Петербург, ЦНИИ РТК, нач.
лаб., к.т.н.
ПОСТРОЕНИЕ
ТРАЕКТОРИЙ ДВИЖЕНИЯ ДЛЯ МОБИЛЬНОГО РОБОТА
Введение
При управлении мобильным роботом возникают три задачи: определение текущих координат
робота (относительно, например, его начального положения), построение
траекторий движения (как для известной, так и для неизвестной карты) и
построение (уточнение) самой карты.
В данной статье рассмотрим вторую задачу: построение
траекторий движения.
Мобильный робот представляет собой колёсную (или
гусеничную) платформу, снабжённую лазерным сканирующим дальномером и датчиками
колёс (спидометрами или одометрами). По своей кинематике платформа может
перемещаться либо по прямой, либо поворачивать на месте (т.н. «танковый поворот»),
то есть, траектория робота – всегда ломаная линия.
Лазерный сканирующий дальномер это прибор, измеряющий
расстояния до непрозрачных препятствий в некотором известном сегменте с
определённой дискретностью (Рис. 1).
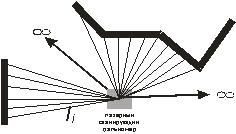
Рис. 1.
Измерение лазерного сканирующего дальномера
На рис. 1 li – расстояние до препятствия в данном направлении;
∞ – направления, в которых нет препятствий.
Для использованного в экспериментах реального
лазерного дальномера LMS-291 немецкой
фирмы «SICK», диапазон измеряемых расстояний которого 0,3 – 80
м., диапазон углов 0 – 180° с дискретностью 0,5°. Погрешность определения расстояний – 5 см.
Строить траекторию движения робота можно только на
известной карте, а во время движения корректировать траекторию в зависимости от
меняющихся условий. Поэтому кроме построения траекторий как таковых, должен
быть реализован алгоритм объезда препятствий. Причем, таких препятствий,
реальные размеры которых полностью неизвестны.
Эти два подхода гарантируют достижение роботом цели,
если цель вообще достижима. Доказать это утверждение можно очень просто,
рассмотрев крайние случаи: если карта совсем неизвестна, то будет работать лишь
алгоритм объезда препятствий, и наоборот, если карта полностью известна, и на
ней нет неучтенных изменений, то будет сразу построена траектория и робот
поедет без использования алгоритма объезда препятствий.
Разумеется, в реальной ситуации робот отрабатывает
движение по траектории не идеально, и время от времени приходится
корректировать его движение. В некоторых случаях даже приходится перестраивать
всю траекторию, чтобы робот мог достичь цели.
Исходя из всего вышеизложенного видно, что есть два
вида траекторий. Первый – когда траектория не является самоцелью, а целью
является достижение роботом определенного положения. То есть, траектория может
быть любой, лишь бы была достигнута цель.
А второй – это когда траектория должна соответствовать
некоторым параметрам. Например, для патрулирующего робота, когда робот должен
обследовать определенную зону, при этом робот также должен в конце пути
достигнуть некоторой заранее известной цели (например, для подзарядки батарей).
Рассмотрим несколько различных способов построения
траекторий на известной карте.
Алгоритм A* (читается: «А со звёздочкой»)
Это модифицированный алгоритм Дейкстры прохода по
графам [3]. Для его применения вначале надо создать т.н. «бинарную» карту, то
есть карту, которая покрыта сеткой, каждая ячейка которой может иметь два
состояния: «занято», если эта ячейка хотя бы частично занята непреодолимым
препятствием, и «свободно», если ячейка полностью лежит вне препятствий.
В простейшем и самом популярном случае сетка имеет
одинаковые ячейки, размер которых равен (или чуть больше – для безопасности)
размеру наименьшего препятствия или размеру робота, если размер робота меньше
наименьшего препятствия:
![]() ,
,
где ![]() - размер ячейки сетки карты;
- размер ячейки сетки карты;
![]() - размер i-того
препятствия;
- размер i-того
препятствия;
![]() - размер робота.
- размер робота.
Разумеется, здесь имеется в виду минимальный размер
препятствия и робота.
Одинаковые ячейки имеют смысл тогда, когда характерные
расстояния между препятствиями сравнимы с самими препятствиями. Если ситуация
иная, то имеет смысл ячейки делать другого размера. Например, если препятствия
малы и расположены редко, то рядом с ними ячейки могут быть сравнимы с
препятствиями, а в незанятых зонах значительно больше их. И наоборот: если
препятствия большие и расположены густо, то ячейки могут быть значительно
мельче препятствий.
Для случая важности самой траектории размер ячейки не
может превышать допустимую дискретность (погрешность) траектории. В этом случае
имеет место некая аналогия с теорией аппроксимации сигналов с ограниченным
спектром. Поэтому, по теореме Котельникова (Найквиста-Шеннона) имеет смысл
задавать размер ячейки не более ½ от допустимой погрешности.
Итак, сетка задана. Для построения на ней графа будем
считать, что середины ячеек – это вершины графа, а переход между ячейками –
дуги. Бывают два вида графов: 4-х связный, кода из ячейки можно перемещаться
лишь влево-вправо и вверх-вниз, и 8-ми связный, кода перемещение возможно еще и
по диагонали.
Рассмотрим общий случай: движение от начального (текущего)
положения в целевое. Это именно общий случай, так как для движения по заранее
известной траектории дискрета траектории и будет той промежуточной целью, куда
требуется переместиться.
Идея алгоритма Дейкстры очень проста. Рассматриваем
вершины графа, являющиеся соседними с текущей (соседние те, в которые можно
перейти за один шаг из текущей). Разумеется, в занятые препятствием вершины мы
перейти не можем. Затем, для каждой из просмотренных вершин, рассматриваем их
соседей и так далее, пока не дойдем до цели. Конечно, для каждого из
«просмотров» нет смысла рассматривать уже пройденные вершины. Поэтому их после
просмотра надо метить, как просмотренные.
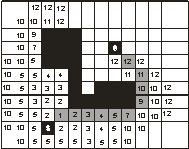
Для иллюстрации предлагается рассмотреть рисунок 2.
|
Рисунок 2 – иллюстрация работы алгоритма Дейкстры
для 8-ми связного графа |
Рисунок 3 – иллюстрация алгоритма А* |
Рисунок 4 – иллюстрация алгоритма движения по
границам препятствий |
На этом рисунке сетка – это сетка карты. Черная
неправильная фигура в центре – препятствие, черные ячейки с буквами «s» - начальное положение, «e» - конечное (целевое) положение. Серые ячейки –
построенная траектория.
Цифрами помечены ячейки, рассмотренные на разных
шагах. Вокруг начального положения ячейки рассмотренные на первом шаге (№1),
далее – на втором (№2) и т.д. Ячейки рассматриваются начиная с правой и далее
по часовой стрелке. На 11-м шаге (№11) попадаем в ячейку, помеченную как
конечная. «Развернуть» траекторию логичнее всего обратно тому, как она была
построена. Поэтому из ячейки с номером n ищем ближайшую ячейку с номером n-1, начиная с «юго-восточной» от неё. Так
восстанавливаем всю траекторию, помня, что целевая ячейка имеет номер 11, а
начальная – номер 0.
Видны
недостатки этого алгоритма. Во-первых, время нахождения траектории сильно
зависит (как M2!) от размера карты. Для такого простого случая, как
на картинке, из 134 свободных ячеек были рассмотрены 103 (более ¾). Во-вторых,
получается не оптимальная траектория, которую затем надо сглаживать, что
является отдельной задачей.
Для ускорения работы существует модификация алгоритма
Дейкстры – алгоритм А*. Он отличается тем, что ячейки, расположенные ближе к
целевому положению, более приоритетны к рассмотрению, чем лежащие дальше. Это
можно представить таким образом, что целевая точка является центром притяжения
жидкости, которая вытекает из начала. Для иллюстрации приведен рисунок 3.
Здесь за 13 шагов рассмотрено 74 точки, что заметно
меньше, чем в предыдущем случае.
Несмотря на минусы, у этих алгоритмов есть и
неоспоримое достоинство: если цель достижима, то эти алгоритмы точно найдут
путь к ней.
Алгоритм «Движение по границам
препятствий»
Этот алгоритм быстр (время расчета зависит от квадрата
количества препятствий), но гарантировать то, что достижимая цель будет найдена
нельзя. Правда, для обычных ситуаций этот алгоритм работает очень надежно. Лишь
для экзотических форм препятствий (т.е. в теории) он дает сбои.
Алгоритм заключается в том, что из текущей точки в
целевую строится прямая и рассматриваются крайние точки ближайшего препятствия,
которое эта прямая пересекает. Эти крайние точки становятся текущими, и все
повторяется снова, пока цель не окажется на прямой видимости.
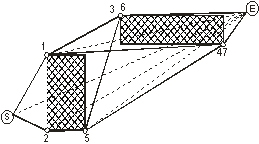
Для иллюстрации рассмотрим рисунок 4.
На рисунке, как принято, буквами s и e,
соответственно, обозначены начальное и целевое положения.
Рассмотрим алгоритм на этом примере:
1. Из начального положения строится прямая в целевую
точку. Эта прямая пересекает препятствие, крайние точки которого обозначены 1 и
2. Точки 1 и 2 становятся текущими.
2. Из точки 1 проводится прямая в целевую точку.
Прямая обозначена 1-е. Прямая 1-е пересекает второе препятствие. Крайние точки
которого обозначены 3 и 4.
3. Из точки 2 также проводится прямая 2-е. Она
пересекает снова первое препятствие. Крайние точки которого 5 и 1. Точку 1
рассматривать нет смысла, так как расстояние s-1 всяко меньше, чем s-2-1.
4. Из точки 5 крайние точки второго препятствия 6 и 7.
5. Так продолжая, получаем четыре ломаных s-1-3-e, s-1-4-e, s-2-5-6-e, s-2-5-7-e. Можно найти
суммарную сложность проезда для каждой ломаной (под сложностью здесь понимаются
затраты ресурсов – топлива, времени и т.п.) и найти минимальную, в смысле
сложности, траекторию.
Достоинства этого алгоритма скорость работы, а
недостаток – при некоторых формах препятствий найти траекторию не
представляется возможным.
Алгоритм «Движение по неплоской
поверхности».
Плоскую карту с наличием препятствий можно представить
как неплоскую поверхность, заменяя препятствия гладкими «холмами». Если проезд
и по свободным от препятствий зонам связан с разными затратами ресурсов
(например, асфальт, проселок, песок, трава, заболоченные местности и т.п.), то
на этой неплоской карте эти зоны также можно задать дополнительными холмами и
впадинами.
Для такого представления карты траектория находится
аналитическими методами. Ранее автором (с соавторами) были рассмотрены способы
решения этой задачи посредством геодезических линий [7]. Но построение
геодезических, к сожалению, занимает очень много вычислительных ресурсов и,
поэтому, выполняется непозволительно долго (для карты порядка 200х200 дискрет –
до минуты!).
Здесь предлагается следующий подход. Существует
гораздо более простой подход: найти траекторию посредством вариационных методов
[5].
Пусть наша рабочая зона (напомню – неплоская)
выражается функцией
![]() ,
,
Где z – «высота» данной точки траектории;
х и у –
декартовы координаты проекции точки поверхности на плоскость.
Требуется минимизировать следующий функционал:
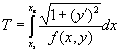
Со следующими предельными условиями:
![]()
где ![]() и
и ![]() - декартовы координаты начальной точки;
- декартовы координаты начальной точки;
![]() и
и ![]() - декартовы координаты конечной (целевой) точки.
- декартовы координаты конечной (целевой) точки.
При разыскании экстремума функционала, требование,
чтобы искомая кривая имела явное уравнение y=y(x) может существенно сузить задачу, так как может
оказаться, что прямые, параллельные оси у, пересекают кривую, дающую решение,
более чем в одной точке[5, стр. 239].
Преобразуем наш функционал для параметрического
задания искомой кривой:
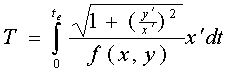 (1)
(1)
с предельными условиями
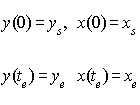
Решение этой задачи сводится к системе двух
дифференциальных уравнений 2-го порядка:
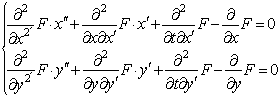 ,
,
где F – подъинтегральное выражение в формуле (1).
Решая эту систему численными методами, было
установлено, что данный подход резко ускоряет нахождение решения: для карты
порядка 200х200 дискрет не более 7 секунд. Это время также может показаться
недопустимо большим, но надо вспомнить, что построение траекторий выполняется
довольно редко.
Заключение.
Рассмотренные в статье методы, при их реализации в
системах управления роботов, показали свою простую реализуемость и надёжность.
Первые методы – проходы по графам имеют 100%-ную надежность, но имеют
неоспоримый минус – высокое время работы. Причём, время их работы порядка N log N (N-количество дискрет карты). Это не даёт применять
алгоритмы прохода по графам для больших карт, где количество ячеек измеряется
десятками тысяч.
Метод прохода по границам препятствий очень быстр лишь
в случае простых препятствий, у которых малое количество «углов». Более того, в
случае, если цель недостижима и количество препятствий с большим количеством
граней велико, то алгоритм может вовсе закончится сбоем – может не хватить
ресурсов вычислителя.
Алгоритм движения по неплоской поверхности имеет кроме
100%-ной надёжности ещё и большое достоинство, что в нём можно учесть разные
коэффициенты проходимости. Минусы очевидны – численное решение уравнений, время
которого сильно зависит от конфигурации поверхности.
1. Springer
handbook of robotics. // Под. ред. Bruno Siciliano,
Oussama Khatib, «Springer» - 2008.
2. С.Ф.Бурдаков,
И.В.Мирошник, Р.Э.Стельмаков. Системы управления движением колесных
роботов. СПб, «Наука»-2001.
3. Т.Кормен,
Ч.Лейзерсон, Р.Ривест. Алгоритмы: построение и анализ. МЦНМО, М-2000.
4. Г.Корн,
Т.Корн. Справочник по математике для научных работников и инженеров. // М.
«Наука» - 1984.
5. В.И.Смирнов.
Курс высшей математики. Том IV. Л., ГИТТЛ –
1951
6. С. Л.
Зенкевич, А.А. Минин. Построение карты мобильным роботом, оснащенным
лазерным дальномером, методом рекуррентной фильтрации. // «Мехатроника,
автоматизация, управление», №8, 2007, стр. 5-12
7. Vasilyev I.A., Lyashin A.M. Control
System of Mobile Vehicle Developed for Cross-Country Motion. // Proc.
«International Symposium on Industrial Electronics 2005», Dubrovnic – Croatia.
P. 173-175.