Сельское хозяйство/2. Механизация сельского хозяйства

Ктн. Патрин В.А., ктн Патрин А.В.

Новосибирский государственный аграрный университет, Россия

Графическая модель движения зерна на плоских решётах

Предложен новый подход в теоретическом описании поведения обрабатываемого зерна на плоских колеблющихся решетах, сочетающий теорию послойного движения зерна с известным графическим методом изучения движения материальной точки, что позволило получить графическую модель наиболее реально отражающую процесс движения зерна на плоских решетах в зависимости от угловой скорости решета, его угла наклона и величины нагрузки зерна. Выявлены три основных фазовых состояний зерна на решете: относительный покой, послойное сдвиговое течение и скольжение зерна по решету, как твердого тела. Доказано, что система «плоское решето – обрабатываемое зерно» обладает элементами самоорганизации и за один полный период колебания решета может иметь восемь сменяющих друг друга, согласованных по времени режимов движения зерна.

Ключевые слова: плоское решето, зерновая среда, послойное течение, сила инерции, приведенный коэффициент трения, графический анализ.

Рабочие органы сортировальных машин и обрабатываемый зерновой ворох представляют сложную диссипативную систему, имеющую способность к авторегулированию и самоорганизации своего состояния в зависимости от действия внешней среды на данную систему.

Это свойство сыпучих сред является одним из самых удивительных явлений природы, которое можно наблюдать при работе плоских и цилиндрических решет.

Теоретически описать и объяснить процесс самоорганизации движения сыпучих сред на рабочих органах сортировальных машин существующим детерминированным или стохастическим методами пока не представляется возможным.

Целю настоящего исследования является использование графического анализа для построения модели движения зерновой среды на плоских решетах и оптимизации процесса работы в зависимости от их конструктивных и кинематических параметров.

Объёкты и методы исследований

Основу предлагаемой графической модели составляет теория послойного движения сыпучей среды В.В. Гортинского [1, 2], где принимаются следующие допущения:

1. Зерновое тело состоит из элементарных слоёв (пластин) толщиной в одно зерно, которые имеют возможность без ограничения смещаться параллельно поверхности решета;

2. Сила сопротивления сдвигу слоя прямолинейно возрастает в зависимости от глубины расположения его в зерновом теле;

В.В. Гортинский [1] предложил приведённый коэффициент трения для любого горизонтального слоя, лежащего внутри сыпучего тела

f_пр = f₀ (1+2εi), f₀ = tg φ, (1)

где f₀ – коэффициент сопротивления сдвигу верхнего слоя (f₀ = 0,645÷0,677);

i = h/н – безразмерная координата рассматриваемого слоя, лежащего на глубине – h при толщине зернового тела равной н;

ε – коэффициент, характеризующий физико-механические свойства зерна (0,156 – 0,215); φ – угол трения зерна.

f_пр – представляет собой удельную силу сопротивления сдвигу элементарной площадки зерна внутри сыпучего тела.

В.В. Гортинский определял f_пр для продуктов переработки пшеницы методом расчета по величине сдвига сыпучей среды в инерционной тележке [2]. Однако данный способ является не точным, поэтому в НГАУ разработан прибор для определения удельной силы сопротивления сдвигу элементарного слоя зерна внутри сыпучего тела, при помощи динамометра с записывающим устройством [3].

В данной работе рассматриваются наклонные решета с горизонтальными колебаниями и плоские сита с круговым возвратно поступательным движением, где движущей силой является сила инерции (ускорение инерции), изменяющейся по гармоническому закону:

j = ω²r · cos(ωt) (2)

где (ωt) – угол поворота и радиус r кривошипа привода решета.

При увеличении ускорения горизонтального решета (α = 0) сдвиговое течение зерна начинается с верхнего слоя при ускорении равном [1]

ω ²₁ r = g f₀ , (3)

Нижний слой, лежащий на горизонтальном решете, сдвинется с учетом уравнения (1), при ускорении решета

ω ²₂ r = g f_пр = g f₀ (1 + 2εi) (4)

В общем случае, когда решето имеет угол наклона – α, то коэффициент трения для верхнего слоя зерна определится по уравнениям [4]

f_0В = sin(α + φ) / cos(α + φ) = tg(α + φ) – вверх по решету; (5)

f_{0 Н} = sin(φ – α) / cos(a – φ) – вниз по решету. (6)

Приведенный коэффициент трения для любого слоя зерна, лежащего внутри зернового тела, определится по уравнениям при движении:

f_прiВ = f_0В (1 + 2εi) – вверх по решету; (7)

f_прiН = f_0Н (1 + 2 εi) – вниз по решету. (8)

Приведенные коэффициенты трения для нижнего слоя зерна обозначены индексами на рисунке 1.

Коэффициенты трения движения зерна на наклонных решётах, представленные в уравнениях (5…8), учитывают составляющую силы тяжести, направленную вдоль поверхности решета и препятствующую сдвигу зерна вверх по решету и, наоборот, способствующую сдвигу его вниз по решету. Графическое пояснение коэффициентов трения верхнего слоя и приведенных коэффициентов трения нижнего слоя для горизонтального – а) и наклонного решета – (б, в) приведены для указанного ниже примера на рисунке 1.

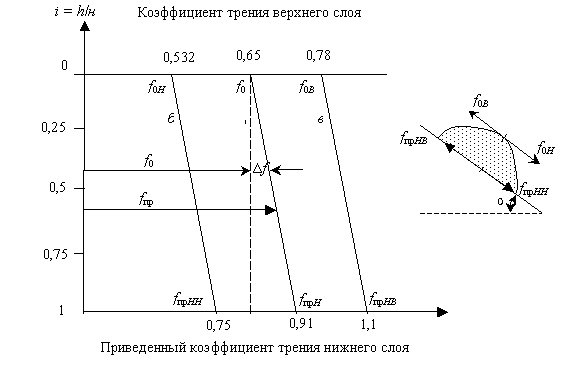
Рис.1. Изменение приведенного коэффициента трения зерна в зависимости от расположения его в зерновом теле: а – горизонтальное решето; б, в – наклонное решето (α = 5°); Δf = 2f₀εi – величина приращения приведенного коэффициента трения.

Ускорение, при котором начинает сдвигаться верхний слой зерна вверх по

наклонному решету равно ω₁² r = g f_0В; (9)

вниз по наклонному решету ω₂² r = g f_0Н. (10)

Ускорение, при котором начинает сдвигаться вверх по наклонному решету нижний слой зерна равно ω₁² r = g f_прНВ; (11)

вниз по решету ω₂² r = g f_прНН. (12)

Построим графическую модель движения зерна на наклонном решете, имеющем следующие параметры: угол наклона решета – a = 5º, угол трения для пшеницы φ = 33º, f₀ = 0,65, толщина слоя зерна на решете н = 0,04 м, коэффициент – ε = 0,2. Все вычисления, выполненные для данного решета по формулам (6 – 13) сведены в таблицу 1, которая представлена ниже.

Проведем вертикальную линию 0 – 0, обозначающую ось колебания решета и горизонтальные линии, указывающие поверхности зернового тела и решета. Величина ускорения, при котором начинает сдвигаться зерновой слой откладывается на графике в масштабе 1 мм = 1 м²/с от оси колебания 0 – 0 по горизонтали для верхнего и нижнего слоя. На графике получим точки аа₁ и вв₁.

Таблица 1

Значений приведенных коэффициентов трения и ускорений решета, при которых сдвигается зерновой слой.

	Горизонтальное решето	Наклонное решето зерно движется
		Вверх	Вниз
Коэффициент трения верхнего слоя зерна	f0 = 0,65	f0В = 0,78	f0Н = 0,532
Приведенный коэффи- циент трения нижнего слоя зерна	fпрН = 0,91	fпрНВ = 1,1	fпрНН = 0,745
Ускорение (м/с^2), при котором начинает сдвигаться:
верхний слой зерна	6,37	7,66	5,22
(отрезок на графике)		0 – а1	0 – а
нижний слой зерна	8,93	10,73	7,3
(отрезок на графике)		0 – в1	0 – в

По второму принятому выше допущению имеем право соединить точки начала сдвига верхнего слоя аа₁ с точками начала сдвига нижнего слоя в, в_1. Наклонные прямые образуют трапецию авв₁а₁ (не заштрихованная область), в которой зерно находится относительно решета в покое и накапливает потенциальную энергию. Горизонтальные отрезки - х₁, х₂ в этой области соответствуют удельной величине сопротивления сдвигу слоя зерна, лежащего на глубине – h_i .

Проведём перпендикулярно поверхности зерна ординату о₁–о₂, на которой отложим в масштабе время периода колебания и кривые изменения скорости и ускорения решета [4].

Если полный период колебания решета выразить отрезком – а (мм) = о₁о₂, то масштаб времени: (с/мм).

Для любого момента времени t положение точки на линии о₁– о₂ и угол поворота кривошипа вверх ψ и вниз θ определяется , или ; , .

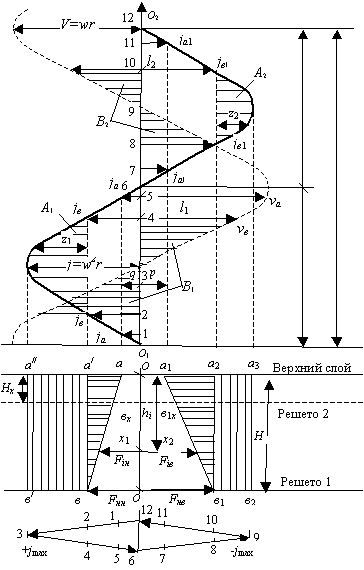
Рис. 2. Графическая модель движения зерна по плоскому решету.

Если амплитуды колебаний скорости ν = wr и ускорения j = w²r выразить отрезками соответственно в (мм) и с (мм), то их масштаб равен μ_ν = wr/в (м/с·мм); μ_j = w²r/с (м/с²·мм), а их величины для любого момента определятся отрезками от оси времени о₁– о₂ до точек на синусоиде и косинусоиде , .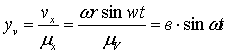

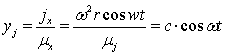Построения, выполненные в масштабе, позволяют на графике определить величины перемещения любого слоя зерна, их скорость и ускорение посредством проектирования точек данного слоя с нижней части рисунка на кривые скорости и ускорения. Параметры движения элементарного слоя в момент его сдвига показаны на кривой ускорения жирными линиями.

Сдвиг слоя возможен, если сила инерции решета становится больше силы сопротивления сдвигу.

Цифры от 1 до 12, расположенные на оси ординат, отмечают отрезки времени, в которых зерновая среда переходит в новое состояние или новый вид движения, им соответствуют цифры, расположенные в нижней части рисунка (на ромбе ускорений) полного периода колебания.

В каждом треугольнике (а– а – в) и (а₁ – а₂ – в₁) за полный период колебания сыпучая среда подвергается послойному сдвигу два раза. Один раз на отрезках времени (1–2) и (7–8) с отставанием от поверхности решета (эффект входа на эскалатор – тело отклоняется назад) и второй раз (4–5) и (10–11) с опережением поверхности решета (эффект схода с эскалатора – тело отклоняется вперед). При этом на отрезках (1–2) и (7–8) сдвиг развивается постепенно, начиная с верхнего слоя по мере увеличения силы инерции решета. Как только нижний слой сдвинется относительно решета, послойное движение прекращается, и всё зерновое тело в точках 2 и 8 начинает скользить относительно поверхности решета в интервале промежутков времени (2–3–4) – левый интервал и (8–9–10) – правый интервал. В точках 3 и 9 решето меняет знак ускорения на обратный. Направление движения решета изменяется в точках 6 и 12 на противоположное.

В точках 4 и 10 ускорение решета резко уменьшается, сила инерции зерна становится больше силы сопротивления сдвигу нижнего слоя; зерновое тело в нижней части тормозится, обеспечивая процесс сдвига слоёв в начальный момент по всей его высоте одновременно, и заканчивается в точках 5 и 11 в верхнем слое. Дальше на участках (5–6) и (11–12) всё зерновое тело находится в относительном покое. Силы инерции уменьшаются настолько, что не обеспечивают послойное сдвиговое течение зерна. Цикл повторяется.

Количественное изменение величины относительного ускорения j_отн всего сыпучего тела по решету определяется на графике в любой момент времени длиной отрезков z₁ в области А₁ – движение в направлении наклона решета и z₂ в области А₂ в направлении его подъёма, а изменение его относительной скорости по решету V_отн определяется на графике длиной отрезков l₁ и l₂ в соответствующих областях В₁ и В₂.

В абсолютных координатах зерновое тело может оставаться неподвижным относительно зерна, движется решето.

Графическая модель позволила выявить четыре вида движения сыпучей среды по плоскому решету в зависимости от его кинематического режима, который можно проследить на рисунке 2, где F_нв, F_нн – силы сопротивления сдвигу нижнего слоя, при движении его вверх и вниз по решету.

1. Если решето имеет ускорение, при котором j_pmax> F_нв, то все циклы движения, как в правом, так и в левом интервалах колебания повторяются, но при движении в сторону подъёма продолжительность относительного покоя при увеличении угла α увеличивается, а время скольжения зернового тела вверх по решету уменьшается.

2. Если ускорение решета, при котором j_max<F_нв>F_нн, то циклы движения сыпучей среды в сторону уклона решета остаются такими же, что и в предыдущем режиме, зерно движется только вниз по решету.

3. Если ускорение решета, при котором j_max<F_нн, то имеет место сдвиговое течение в верхних слоях зернового тела. Перемещение зерна относительно поверхности решета отсутствует, следовательно, прекратится и прохождение мелких частиц через отверстия решета.

4. Если j_max< gf₀, то всё зерновое тело находится в относительном покое и в абсолютном движении перемещается вместе с решетом.

Таблица 2

Циклы движения зерна на плоском решете за время одного периода колебания

Время цикла на графике		Характеристика циклов
вниз	вверх
0–1	(6–7)	Относительный покой, сепарация отсутствует, в сыпучей среде накапливается потенциальная энергия.
1–2	(7–8)	Первое послойное течение зерна, идёт процесс самосепарации. Мелкие частицы перемещаются к поверхности решета. Потенциальная энергия переходит в кинематическую сдвига зерна.
2–3–4	(8–9–10)	Всё сыпучее тело, как единое целое, скользит относительно поверхности решета. Мелкие частицы проходят через отверстия решета.
4–5	(10–11)	Второе послойное течение зерна. Идёт процесс самосепарации. Мелкие частицы перемещаются к поверхности решета.
5–6	(11–12)	Относительный покой. Идёт накопление потенциальной энергии. Сепарация отсутствует.

Графическая модель позволяет анализировать работу решета при разных нагрузках зерна, для этого достаточно задать на рисунке новую толщину слоя H_x, провести горизонтальную линию, которая даёт новую поверхность решета (решето 2). Из точек в_х и в_1х восстановить перпендикуляры, которые образуют новые треугольники сдвигового течения зерна, а за ними и область перемещения зерна по решету.

Выводы:

1. Предложенная графическая модель, позволяет определить влияние управляющего параметра (угловой скорости привода решета), нагрузки и угла наклона решета на режимы движения и фазовое состояние зерна.

2. Доказано, что система «плоское решето – обрабатываемое зерно» обладает элементами самоорганизации. За один период колебания решета зерно меняет восемь раз следующие фазы своего движения: относительный покой, послойное сдвиговое течение внутри зернового тела и свободное его перемещение относительно поверхности решета.

3. В отличие от известного графического анализа, при котором рассматривается движение материальной точки по плоскому решету, предлагаемая модель позволяет анализировать движение всей зерновой среды по решету, в зависимости от его конструктивных и кинематических параметров.

Литература:

1. Гортинский В.В. Процессы сепарирования на перерабатывающих предприятиях/ В.В.Гортинский, А.Б. Демской, М.А. Борискин, - М.,1980.-300с.

2. Гортинский В.В. Сортирование сыпучих тел при их послойном движении по ситам / В.В.Гортинский // Труды ВИМ. - М.,1964. Т. 34. - С. 121 – 190.

3. Патент на изобретение № 2459906 «Способ и устройство для измерения силы сопротивления сдвигу слоев в сыпучем теле» от 10.05.2012 Бюл. №13 / Патрин В.А., Крум В.А..

4. Летошнев М.Н. Сельскохозяйственные машины. Теория, расчет, проектирование и испытание. – М,- Л., 1955 – 764с.