Биярова Амангуль Онербаевна, к.э.н., доцент,

Казахский экономический университет им. Т.Рыскулова, Казахстан

АНАЛИЗ БЛАГОСОСТОЯНИЯ ПОТРЕБИТЕЛЕЙ

Аннотация

Настоящая статья рассматривает условия экономики благосостояния при достижении потребителями максимума своей полезности. В статье описываются эффективные векторы потребления, которые назначаются таким образом, что ни один потребитель не может увеличить свою полезность, не ущемляя при этом интересов других потребителей.

Ключевые слова: благосостояние, потребители, состояние равновесия.

Abstract

This article examines the conditions of welfare economics when it reaches its maximum utility consumers. This article describes the effective consumption vectors, which are assigned in such a way that no one user can not increase its usefulness, without prejudice to the interests of other consumers.

Keywords: welfare, consumersequilibrium.

Модели равновесия являются дескриптивными, а не нормативными; их роль заключается в описании взаимодействий между спросом, предложением и ценами в экономике с конкуренцией. Напротив, теория экономики благосостояния является нормативной; она ставит своей задачей нахождения векторов производства и потребления, дающих оптимальные результаты с определенной точки зрения потребителя. Теория равновесия рассматривает вещи как они есть, теория благосостояния – вещи какими они могли бы стать.

Целью экономики благосостояния является система, в которой все потребители достигают максимума своей полезности. Если мы рассматриваем систему, в которой участвует более одного потребителя, то это случается довольно редко. В этом случае мы характеризуем эффективные векторы потребления, которые назначаются таким образом, что ни один потребитель не может увеличить свою полезность, не ущемляя при этом интересов других потребителей. Это понятие известно под названием оптимума Парето. Дескриптивное изучение экономики можно охарактеризовать при помощи явления равновесия. Состояние равновесия – это такое положение, когда при заданном наборе цен ни один потребитель не может приобрести больше без дополнительных затрат и ни один производитель не может добиться большей прибыли. Изучение экономики благосостояния связанно с проблемой описания тех состояний экономики, когда ни один потребитель не может стать богаче, не обедняя при этом другого.

Наборы товаров есть r-мерные векторы. Каждому потребителю i (i=1,m) соответствует множество X_i векторов потребления из E^r. Функция полезности U_i(x_i), x_iX_i характеризует предпочтению i-го потребителя. Экономика достигает совершенства, когда все потребители могут одновременно добиться максимума своей функции полезности [1]. Мы увидим, что уравнение конкурентной экономики, вообще говоря, не позволяет достичь каждому потребителю максимальной полезности.

Говорят, что система векторов {x_i} (x_iX_i) образует оптимум Парето, если а) эта система допустима и б) не существует другой системы векторов
, для которой

,

причем хотя бы для одного потребителя имеет место строгое неравенство.

Рассмотрим сначала вопрос о том, когда оптимум Парето является конкурентным равновесием, и обратно.

Случай одного потребителя: Пусть – подмножества пространства E^r, представляющее множества возможных векторов производства фирмы j. Очевидно,

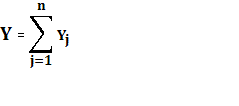
образует множества векторов суммарного производства для экономики.

Пусть Х (лежащее в положительном ортанте E^r) представляет множества потребления, доступное нашему потребителю, а через U(x) обозначена его функция полезности (строго вогнутая). Пусть множество суммарного производства выпукло и компактно. Потребитель выбирает , чтобы

, для которых существуют такие векторы

Любой вектор , для которого существует такой вектор назовем допустимым. То есть потребитель, выбирая допустимый вектор максимизирует свою функцию полезности, возможности, действуя при этом с учетом имеющихся технологических возможностей. Из-за компактности Y область допустимых векторов x (x≤y) также компактно.

I. Существуют векторы для которых

II. Для каждого существует такой вектор .

Это означает, что если отвлечься от бюджетных ограничений и допустимости, то не существует вектора потребления, который являлся бы точкой насыщения. Задача определения оптимального вектора потребления можно свести к задаче вогнутого программирования [1].

Для пары {x,y} (из X × Y) положим

g(x,y)=U(x), F(x,y)=(y₁ – x₁ …..,y_r – x_r).

Тогда

max g (x,y) = max U(x) (1)

при условиях

F (x,y) ≥ 0 (xX, yY). (2)

Определение конкурентного равновесия в случае одного потребителя имеет вид: система векторов , где y^*Y, x^*X, а p^* - вектор относительных цен,

образует конкурентное равновесие, если

U(x^*) = maxu(x), (3)

xX

где

(p^* ,y)= max (p^*,y) (4)

yY

и x^*≤y^* , (p^*, x^* - y^*) =0 (5)

Пусть выполнены условия I и II. Для того чтобы вектор х^* максимизировал U(x) среди всех допустимых векторов, необходимо и достаточно существование вектора y^*Y и вектора цен p^*, при которых {p^*,x^*,y^*} образует конкурентное равновесие.

Пусть х^* максимизирует U(x) по всем допустимым векторам. Выберем любой вектор y^*Y, для которого y^*≥x^*, тогда пара {x^*,y^*} является решением задачи (1), (2). Функция Лагранжа[1]

φ(x,y,u) = g(x,y) + (u, F(x,y)) = U(x) + (u, F(x,y)),

где {x,y} XxY, au≥0, имеет седловую точку {x^*,y^*,u⁰}, для которой

U(x) + (u⁰, F(x,y)) ≤ U(x^*) + (u⁰, F(x^*,y^*)) ≤ U(x^*) + (u,F(x^*,y^*)) (6)

Далее

F(x^*,y^*) ≥ 0, (u⁰ , F(x^*, y^*)) =0. (7)

Полагаем, что u⁰≥0, так как в противном случае левое неравенство в (6) противоречило бы условиюII. Положим p^* =u⁰, где

Установим теперь, что тройка {x^*,y^*,p^*}образует конкурентное равновесие. Из (7) следует (5). Так как

(u⁰ , F(x,y))=(1/) [(p^*,y) – (p^*,x)],

мы находим из (7) и левого неравенства (6), что U(x^*) ≥ U(x) в согласии с (3) Используя снова левое неравенство (6) для конкретного выбора {x,y}={x^*,y} при произвольном yY, мы проходим к неравенству

(u⁰,y) ≤ (u⁰, y^*),эквивалентному (4).

Обратно, пусть {x^*,y^*,p^*} определяет конкурентное равновесие в смысле (3)-(5). Покажем что U(x^*)= maxU(x) где максимум взят по всем допустимым векторам х. Для любого допустимого х существует некоторый yY, такой, что y≥x. Следовательно (p^*,y) ≥ (p^*,x). Кроме того (p^*,y^*) ≥ (p^*,x) в силу (4). По этому, согласно (3) U(x^*) ≥ U(x), что и требовалось.

Случай многих потребителей: Пусть X_iE^r множество потребления для потребителя i,(i=1,m), и

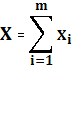
множество суммарного потребления всех потребителей. Упорядочение предпочтения для потребителей i описывается строго вогнутой функцией полезности U_i(x_i). Пусть все множества X_i лежат в неотрицательном ортанте пространства E^r , выпуклы и замкнуты.

Найдем условия того, чтобы оптимум Парето было элементом конкурентного равновесия. Говорят, что система векторов образует конкурентное равновесие, если p^* представляет собой вектор относительных цен, для которого

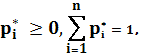
и данная система удовлетворяет условиям

(1)

(2)

где

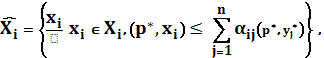
и

x^* ≤ y^* , (p^*, x^* − y^*)=0, (3)

где

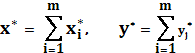
Чтобы характеризовать оптимум Парето определим для любого набора {x₁,…,x_m; y₁,…y_n} (x_iX_i, y_jY_j) вектор функцию

G(x₁,…,x_m; y₁,…y_n) = {U_i (x_i)} = U(x). (4)

Пусть F(x₁,…,x_m; y₁,…y_n) = y−x,(5)

где

Характеризация оптимум Парето эквивалентно характеризации всех эффективных точек U(x) при условиях F≥0, x_iX_i, y_jY_j .

Величины α_ij представляют собой долю прибыли, которая выделяется i-му потребителю [1]. Предполагается, что

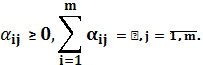
Условия I и снова II остается.

Пусть выполнены условияI и II. Пусть - такой оптимум Парето, что еслиy^*≥x^* , то для любого i₀ существует такая система векторов потребления, что и существует некоторый вектор для которого

Тогда существуют такие векторы вектор цен p^* и матрица

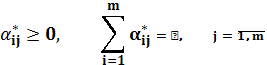
что система

образует конкурентное равновесие.

Если есть конкурентное равновесие, то представляет собой оптимум Парето.

Для выделения конкурентного оптимума Парето необходимо установить некоторые дальнейшие критерии. Один из них известный под названием принципа справедливости, заключается в назначении равных весов
и в определении такихx_iX_i , при которых сумма

достигает максимума, причем x_iподчинены ограничениям x_iX_i и существует такой вектор yY, для которого

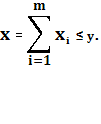
Получаемые таким образом векторы образуют оптимум Парето.

Литература:

1.А.О. Биярова. Моделирование рыночной экономики: Учебное пособие. – Алматы: Экономика, 1999.