УДК.517.956

Колісник Р.С., Шевчук Н.М.

Властивість локалізації розв’язку еволюційного рівняння з гармонійним осцилятором

Розглянемо рівняння

(1)

де - гармонійний осцилятор, тобто оператор, породжений в гільбертовому просторі диференціальною операцією . Відомо [1], що - невід’ємний самоспряжений оператор в з суто дискретним спектром: ; відповідними власними функціями є функції Ерміта , які утворюють ортонормований базис в . При цьому простір

який відноситься до просторів типу , введених в [2], співпадає з множиною

аналітичних векторів оператора (див. [1]). Зазначимо, що складається з тих й лише тих функцій , які допускають аналітичне продовження у всю комплексну площину і для яких справджується нерівність з деякими сталими .

Символом позначатимемо простір, топологічно спряжений до , а його елементи – лінійні неперервні функціонали, задані на , називатимемо узагальненими функціями. Із теорії формальних рядів Фур’є, розвиненої в [1] випливає, що простори та можна розуміти як простори рядів Фур’є-Ерміта 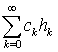, де - коефіцієнти Фур’є-Ерміта функції (функціоналу ), задовольняють відповідно умови:

а) ;

б)

(тут позначає дію функціоналу на основну функцію ; при кожному ).

Під розв’язком рівняння (1), слідуючи [1], розумітимемо функцію , яка задовольняє умови: 1) при кожному ; 2) диференційовна по при кожному ; 3) задовольняє рівняння (1). Із результатів наведених в [1] випливає, що функція є розв’язком рівняння (1) тоді й лише тоді, коли вона подається у вигляді

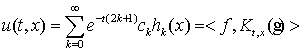, (2)

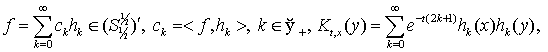
при кожному та ; граничне значення при існує в просторі , тобто

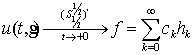. (3)

Ця властивість дозволяє ставити задачу Коші для (1) так: знайти розв’язок рівняння (1), який задовольняє початкову умову

, (4)

в сенсі (3). Задача Коші (1), (4) коректно розв’язна; її розв’язок зображається формулою (2).

Якщо розглянути простір

, де - фіксований параметр, то, як відомо (див. [2]), в цьому просторі є фінітні функції. Звідси випливає, що має зміст таке означення: узагальнена функція , дорівнює нулеві на інтервалі , якщо для довільної функції , носій якої міститься в . Отже, важливо вивчити питання про можливість “локального” покращення збіжності розв’язку задачі Коші (1), (4) до якщо і співпадає на інтервалі з неперервною функцією, то чи буде розв’язок збігатися до у звичайному розумінні (поточково або рівномірно) на інтервалі ? Основний результат цього повідомлення складає позитивна відповідь на поставлене питання. Наведемо одне допоміжне твердження, яке використаємо при доведенні сформульованої властивості.

Лема. Для функції правильним є зображення , причому , (5)

де - фіксоване, .

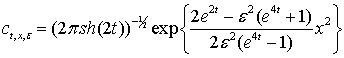Доведення леми використовує відомий розклад (див.[3])

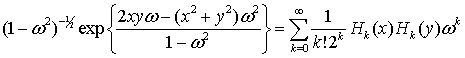, (6)

, в якому слід покласти , а також оцінки функцій Ерміта комплексного аргументу 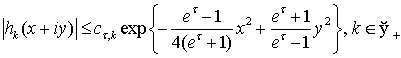, , 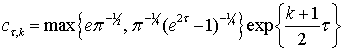де - довільно фіксований параметр, наведені в [4] (в (6) , - стандартизовані многочлени Ерміта, див. [3]).

Теорема (властивість локалізації). Нехай - розв’язок задачі Коші (1), (4) з початковою функцією . Якщо узагальнена функція дорівнює нулеві на інтервалі , то при рівномірно відносно на довільному відрізку .

Доведення. Нехай . Візьмемо відрізок так, що і побудуємо функцією , з носієм в , рівну одиниці на . Оскільки , як функції (при кожному ), належать до простору , то правильною є рівність , де . Узагальнена функція дорівнює нулеві на інтервалі , supp, тому . Тоді з властивості лінійності функціоналу випливає, що .

Для доведення твердження досить встановити, що множина функцій обмежена в просторі , рівномірно по , для досить малих значень , і , тобто

, (7)

де сталі не залежать від , які змінюються вказаним способом. Оскільки на , то оцінку (7) досить одержати для .

Оскільки , то

. (8)

Отже, використавши формулу диференціювання добутку двох функцій, оцінки (5), (8) дістанемо, що

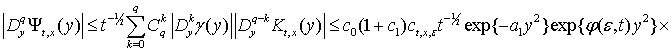
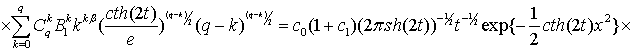
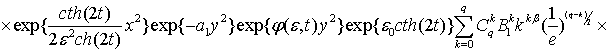
, де - довільно фіксоване число. Візьмемо тепер , де - фіксований параметр і скористаємося такими співвідношеннями:

, .

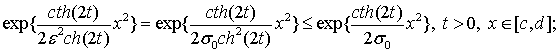
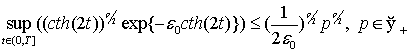Тоді .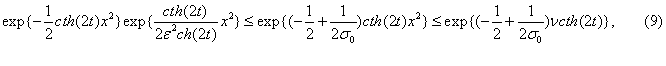

Далі вважатимемо, наприклад, що . Врахувавши (9), дістанемо наступну оцінку:

.

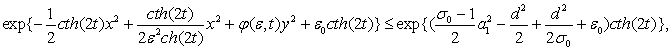
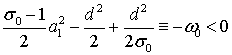Нескладно підрахувати, що якщо взяти , то , де . Отже, якщо тепер покласти , то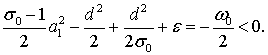

_Тоді

(тут враховані такі співвідношення еквівалентності:).

Остаточно дістаємо оцінку

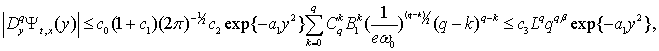де , причому всі сталі не залежать від . Інші випадки розміщення інтервалу на числовій прямій розглядаються аналогічно.

Теорема доведена.

Наслідок. Нехай - розв’язок задачі Коші (1), (4) з початковою узагальненою функцією . Якщо збігається на інтервалі з неперервною функцією , то при рівномірно відносно на довільному відрізку .

Література

1. Горбачук В.И., Горбачук М.Л. Граничные задачи для дифференциально-операторных уравнений. – Киев: Наук. думка, 1984. – 283с.

2. Гельфанд И.М., Шилов Г.Е. Пространства основних и обобщенных функций. – М.: Физматгиз, 1958. – 307с.

3. Суетин П.К. Классические ортогональне многочлены. – М.:Наука, 1976. – 328с.

4. Городецький В.В. Множини початкових значень гладких розв’язків диференціально-операторних рівнянь параболічного типу. – Чернівці: Рута, 1998. – 219с.