К.ф.м.н. Морозова Л.Е.

Ижевский государственный технический университет

имени М.Т. Калашникова

Об асимптотике квазиуровней двухчастичного оператора Шредингера

Рассмотрим двухчастичный дискретный оператор Шредингера действующий в пространстве . Здесь определяется формулой

Предполагаем, что функция ненулевая, вещественная и удовлетворяет оценке

Операторы подобного вида возникают при описании транспорта электронов через наноразмерные электронные устройства (см. например [1], [2]), а также в теории спиновых волн при решении уравнения Гейзенберга с помощью анзаца Бете для одномагнонных состояний (состояний с одним перевернутым спином) в цепочках атомов [3]. В данной работе изучается спектр, а также собственные значения и резонансы оператора .

Рассмотрим унитарный оператор определяемый формулой

где параметр называется квазиимпульсом. C помощью отображения можно разложить оператор в прямом интеграле пространств

Следовательно, исследование оператора эквивалентно исследованию семейства операторов действующих при фиксированном в пространстве .

Спектр оператора совпадает с отрезком Так как представляет относительно компактное возмущение оператора то согласно [4] существенный спектр оператора совпадает со спектром оператора Ядро резольвенты оператора имеет вид (см. [5])

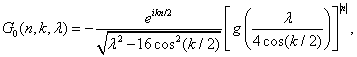
где обратная функция к функции Жуковского. Функция аналитически продолжается по на двухлистную риманову поверхность определяемую функцией листы которой склеиваются вдоль

Уравнение на собственные значения оператора в области, где существует резольвента , можно записать в виде

(1)

где Для того чтобы, оставаясь в пространстве , исследовать также резонансы, переходим к новой функции тогда уравнение (1) примет вид

(2)

Определение 1. Число принадлежащее второму листу римановой поверхностибудем называть резонансом оператора , если существует ненулевое решение уравнения (2).

Определение 2. Квазиуровнем оператора будем называть его собственное значение или резонанс.

Определение 3. Кратностью квазиуровня будем называть

Доказана следующая

Теорема. Предположим, что Тогда в некоторых окрестностях точек для всех достаточно малых существует ровно по одному квазиуровню кратности единица оператора для которых справедлива формула

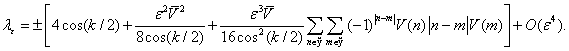
При этом квазиуровень, расположенный вблизи точки (соответственно ), является при собственным значением (соответственно, резонансом), а при - резонансом (соответственно, собственным значением).

Литература.

1. Miroshnichenko A.E., Kivshar Y.S. Engineering Fano rezonances in discreate arrays. Phys. Rev. E. 2005. V. 72, 056611 (7p).

2. Torio M.E., Hallberg K., Ceccatto A.H., Proetto C.R. Kondo resonances and Fano antiresonances in transport through quantum dots. Phys. Rev. B. 2002. V. 65, 085302-1-085302-5.

3. Изюмов Ю.А., Скрябин Ю.Н. Статистическая механика магнито-упорядоченных систем. M.: Наука, 1987. 264 c.

4. Рид М., Саймон Б. Методы современной математической физики. Т.4. Анализ операторов. М.: Мир, 1982. 428 c.

5. Baranova L.E. Chuburin Yu.P. Quasi-levels of the two-particle discrete Schrödinger operator with a perturbed periodic potential. J.Phys.A: Math.Theor. 2008. V. 41, \No. 435205 (11pp).