Математика/1.Дифференциальные и интегральные уравнения

К.ф.-м.н. Мартинюк О. В.

Чернівецький національний університет імені Юрія Федьковича,Україна

Про розв’язність задачі Коші для еволюційних рівнянь з операторами узагальненого диференціювання

Питання про зображення лінійних неперервних відображень у вигляді операторів узагальненого диференціювання та інтегрування скінченного та нескінченного порядків вивчається у теорії аналітичних у крузі функцій. Оператори Гельфонда-Леонтьєва, які введені в середині 20 сторіччя при вивченні розкладів цілих функцій в узагальнені ряди Фур’є, утворюють важливий клас операторів узагальненого диференціювання та інтегрування. Властивості таких операторів досліджували і продовжують досліджувати математики в просторі однозначних і цілих в функцій з топологією компактної збіжності ( не є нормованим простором, але в той же час – простір Фреше). Прикладами інших просторів, елементами яких є цілі функції і які використовуються при дослідженні проблеми про класи єдиності та класи коректності задачі Коші для рівнянь з частинними похідними є простори типу – простори , , введені І.М. Гельфандом та Г.Є. Шиловим в [1], а також простори типу , введені Б.Л. Гуревичем [2] (див. також [3]), в яких для характеристики поведінки функцій на нескінченності замість степеневих використовуються опуклі функції. Топологія вказаних просторів відмінна від топології простору , функції з таких просторів на дійсній осі разом з усіма своїми похідними при спадають швидше, ніж , , .

В [4] досліджені простори , які будуються за певними послідовностями та і котрі є узагальненнями просторів , що будуються за послідовностями , , , , [5]. У цій роботі встановлюється розв’язність задачі Коші для еволюційних рівнянь з операторами узагальненого диференціювання в просторах .

Нехай – ціла функція, коефіцієнти якої задовольняють умову

– фіксоване).

Визначимо оператор узагальненого диференціювання Гельфонда-Леонтьєва в просторі за формулою , де , – довільна функція з простору . Так визначений оператор для довільно фіксованого неперервно відображає простір в себе [4].

Прикладом оператора , який діє в просторі , може служити оператор, побудований за цілою функцією

де – поліном: , причому , (якщо , то ). У цьому випадку [6]

де коефіцієнти мають спеціальний вигляд.

Нехай , , – деяка ціла функція. Говоритимемо, що в просторі задано оператор узагальненого диференціювання Гельфонда-Леонтьєва нескінченного порядку , якщо для довільної основної функції ряд

зображає деяку функцію з простору .

Якщо ціла функція задовольняє умову

(1)

де 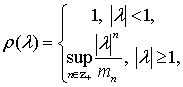то в просторі визначений оператор , який неперервно відображає в [4].

Наприклад, функція , , де – фіксований параметр, задовольняє умову (1). Справді, скориставшись властивостями опуклих функцій (функція є опуклою на ) знайдемо, що

де , якщо , – довільне фіксоване число і , якщо . Отже, в просторі визначений і є неперервним оператор

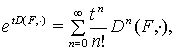
який відображає простір в себе. У просторі визначений і є неперервним також оператор , тобто для функції ряд

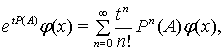(2)

де , , зображає функцію , яка при кожному є елементом простору [4]. Звідси випливає, що елементом простору є також функція , .

Нехай позначає частинну суму ряду (2). Тоді при за топологією простору . Отже,

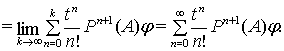(3)

У просторі розглянемо задачу Коші

(4)

, (5)

де – оператор, визначений вище.

Під розв’язком задачі (4), (5) розумітимемо функцію , диференційовну по , яка при кожному є елементом простору , задовольняє рівняння (4) і початкову умову (5) в тому сенсі, що при за топологією простору ; при цьому неперервно залежить від .

Правильним є наступне твердження.

Теорема. Задача Коші (4), (5) розв’язна в просторі (у вказаному розумінні); розв’язок цієї задачі дається формулою

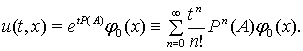
Доведення. Введемо позначення ,

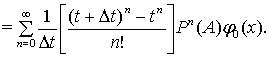
Доведемо, що функція , як абстрактна функція параметра із значеннями в просторі (означення абстрактної функції див. в [1]), диференційовна по у кожній точці . Зафіксуємо довільно і знайдемо елемент такий, що при у просторі , або, що при у просторі . Це означає наступне: сім’я функцій рівномірно (по ) збігається до нуля при в будь-якій обмеженій області і при цьому справджується оцінка

(6)

зі сталими , , , не залежними від .

Доведемо, що

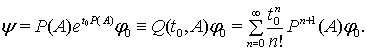
Користуючись теоремою Лагранжа про скінченні прирости знайдемо, що

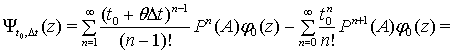
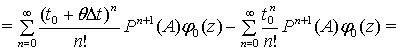
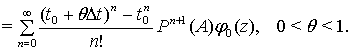
Звідси та з (3) випливає, що при кожному , тобто нерівність (6) виконується з певними сталими , , , якщо вважати, що .

Якщо , де – обмежена область в , то правильними є нерівності

де , , (див. [4]). Для досить малих значень

.

Отже, , , де 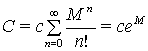, . Звідси випливає, що при рівномірно по .

Цим доведено, що

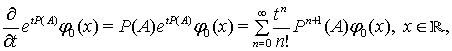
тобто функція є розв’язком рівняння (4).

Функція , як абстрактна функція параметра із значеннями в просторі , диференційовна по , а, отже, і неперервна по у кожній точці , тобто

за топологією простору . Зокрема, при у просторі , що й потрібно було встановити.

Якщо і при у просторі , то з властивості неперервності оператора у цьому просторі (при фіксованому ) випливає співвідношення

що й означає неперервну залежність від .

Теорема доведена.

Зауваження. Аналогічний результат має місце у випадку, коли в рівнянні (4) , де , а початкова умова має вигляд . Розв’язок такої задачі Коші дається формулою

,

Література:

1. Гельфанд И.М. Пространства основных и обобщенных функций / И.М. Гельфанд, Г.Е. Шилов. – М.: Физматгиз, 1958. – 307 с.

2. Гуревич Б.Л. Некоторые пространства основных и обобщенных функций и проблема Коши для конечно-разностных схем / Б.Л. Гуревич // Докл. АН СССР. – 1954. – Т. 99, № 6. – С. 893-896.

3. Гельфанд И.М. Некоторые вопросы теории дифференциальных уравнений / И.М. Гельфанд, Г.Е. Шилов. – М.: Физматгиз, 1958. – 274 с.

4. Городецький В.В. Задача Коші та двоточкова задача для еволюційних рівнянь із операторами узагальненого диференціювання / В.В. Городецький, О.В. Мартинюк // Доповіді НАН України. – 2013. – № 3. – С. 7-13.

5. Горбачук В.И. Граничные значения решений дифференциально-операторных уравнений / В.И. Горбачук, М.Л. Горбачук. – К.: Наук. думка, 1984. – 283 с.

6. Леонтьев А.Ф. Обобщения рядов экспонент / А.Ф. Леонтьев. – М.: Наука, 1981. – 320 с.