УДК 519.3                                                                                                         Хомченко А.Н.

Черноморский государственный университет им. Петра Могилы, г. Николаев, Украина

Задачи Дуба для одномерного уравнения Пуассона и квадратуры Гаусса

Введение.

Рассматриваются задачи хронометрирования одномерных случайных блужданий в канонических(стандартных) интервалах [0,1] и [-1,1] с поглощающими узлами на концах. Эту задачу сформулировал американский математик Дж. Дуб (1953г.), который показал, что математической моделью этого случайного процесса служит уравнение Пуассона со специальной правой частью и однородными граничными условиями.

В одномерном случае эта задача достаточно проста, однако ее решение удивительным образом ассоциируется с красивыми результатами гениального немецкого математика К. Гаусса и выдающегося французского физика и математика С. Пуассона. В связи с квадратурами Гаусса мы не можем не вспомнить о Бернулли и Лежандре, которые по праву являются соавторами высокоточных формул приближенного интегрирования. Нули полиномов Бернулли и Лежандра помогли Гауссу правильно выбрать узлы интегрирования соответственно на [0,1] и [-1,1].

Анализ предшествующих, публикация.

Здесь мы сошлёмся только на те источники, которые имеют непосредственное отношение к теме. Прежде всего это книга [1], в которой формулируются и решаются задачи о случайных процессах. Квадратурные формулы Гаусса-Лежандра можно найти в [2-4]. Квадратуры Гаусса-Бернулли на [0,1] легко получаются из формул Гаусса-Лежандра, если узлы интегрирования расположить в нулях полинома Бернулли. Ниже это показано на примере квадратуры с двумя узлами (обобщение формулы трапеций).

Основная часть. Начнем с интервала [0,1]. Поставим задачу: на интервале [0,1] найти функцию  , удовлетворяющую уравнению Пуассона.

                                                                                               (1)

и граничным условиям                                                     (2)

Предварительный анализ (1) и (2) показывает, что график - это квадратичная парабола с ветвями вниз, пересекающая ось  в точках  и . С вероятностной точки зрения - функция случайного аргумента. Случайный аргумент  -точка  старта броуновской частицы, блуждающей в [0,1]. По всем траекториям, начинающимся в точке , - среднее время выхода траектории на границу интервала. В теории случайных процессов доказано, что все траектории с вероятностью 1 заканчиваются на конце интервала(на каком именно – дело случая).

Путем повторного интегрирования (1) с учетом условий (2) получим

                                                                                          (3)

На рис.1 изображен график .

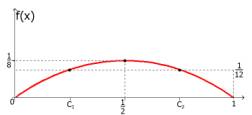
Рис.1 График функции (3).

Интересно определить математическое ожидание , т.е. среднее время выхода на границу для всех траекторий, начинающихся внутри [0,1]. По теореме о среднем в интегральном исчислении получаем

С геометрической точки зрения  – средняя аппликата  на [0,1]. Это означает, что площадь криволинейной трапеции (рис.1) в точности равна площади прямоугольника с основанием 1 и высотой .

Полезную информацию дают точки пересечения прямой  и кривой . Абсциссы точек пересечения  и  находим из уравнения

Любопытно, что график квадратичного полинома Бернулли пересекает ось  именно в этих точках. Гаусс показал, что приближенная формула интегрирования с двумя узлами(формула трапеций) имеет наивысшую алгебраическую степень точности, если узлы интегрирования помещены в точках  и  .

Задача Дуба на интервале [-1,1] практически не отличается от изложенной выше. Поскольку изменился только интервал – носитель функции , алгоритм построения решения уравнения Пуассона и поиска высокоточных узлов квадратуры Гаусса сохраняется.

В это случае решение задачи Дуба имеет вид

                                                                                         (5)

Нетрудно убедится, что функция (5) удовлетворяет уравнению (1) и граничным условиям

                                                                                         (6)

График этой функции показан на рис.2.

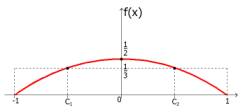
Рис.2 График 

Математическое ожидание , т.е. среднее время выхода на границу для всех траекторий, начинающихся внутри [-1,1]:

Это средняя аппликата   на [-1,1]. Как обычно нас интересуют точки пересечения кривой  и прямой  . Абсциссы   и   находим из уравнения:

В этих точках график квадратичного полинома Лежандра пересекает ось . И только эти точки обеспечивают точное совпадение площади криволинейной трапеции и площади прямоугольника с основанием 2 и высотой  (рис.2).

Таким образом, мы имеем две версии высокоточной формулы трапеций:

квадратура Гаусса-Бернулли

где ,

и квадратура Гаусса-Лежандра

где .

Напомним, что модель Ньютона-Котеса жестко требует, чтобы узлы интегрирования в формуле трапеций располагались на концах интервала. Модель Гаусса смягчает требования к расположению узлов интегрирования. Сопоставление двух моделей (Ньютона и Гаусса) дает наглядное представление о «жестком» и «мягком» математическом моделировании (по терминологии В.И. Арнольда). Сегодня перспективное направление «мягкого» математического моделирования остро нуждается в убедительных и наглядных примерах.

Представляет интерес обобщение формул Гаусса на двойные и тройные интегралы. Такие формулы находят применение в методе конечных элементов [2,3].

 

Литература:

1.                                                                                                                                                                                                                                                                                     Дуб Дж.Л. Вероятностные процессы / Дж.Л. Дуб. – М.:ИЛ, 1956 – 605с.

2.                                                                                                                                                                                                                                                                                     Зенкевич О. Конечные элементы и аппроксимация / О. Зенкевич, К. Морган. – М.: Мир, 1986 – 318с.

3.                                                                                                                                                                                                                                                                                     Математика и САПР: В 2-х кн. Кн.2 / П. Жермен-Лакур, П.Л. Жорж, Ф. Пистр, П. Безье, - М.: Мир, 1989.–264с.

4.                                                                                                                                                                                                                                                                                     Шуп Т. Решение инженерных задач на ЭВМ / Т.Шуп. – М.: Мир, 1982.– 238с.