И.А. Долгарев

СВОЙСТВА КВАДРАТИЧНЫХ ФОРМ ПОВЕРХНОСТЕЙ

3-МЕРНОГО ПРОСТРАНСТВА-ВРЕМЕНИ ГАЛИЛЕЯ

Указаны поверхности пространства-времени Галилея, для которых коэффициенты второй квадратичной формы выражаются через коэффициент первой квадратичной формы. Приведена основная теорема галилеевой теории поверхностей и некоторые свойства изгибаемости поверхностей.

1. Определяемость поверхности коэффициентами ее квадратичных форм

1.1. Пространство-время Галилея

В линейном пространстве аффинного пространства задается галилеево скалярное произведение векторов: пусть , ; их галилеево скалярное произведение равно

В результате получается галилеево векторное пространство , аффинное пространство превращается в галилеево пространство-время , [1, c. 32 – 33]. Галилеев скалярный квадрат вектора находится при . Галилеева норма вектора есть

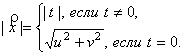(1)

Векторы составляют 2-мерное евклидово пространство . Компоненты векторов и точек называются пространственными. Компонента векторов и точек называется временной. Точки называются событиями. Множество всех событий составляет мир, совпадает с . Множество событий , одновременных с событием , составляет в пространстве-времени евклидову плоскость , т.к. . Через каждую точку в пространстве-времени проходит единственная евклидова плоскость. Векторы , , называются галилеевыми. Векторные функции = дифференцируются покомпонентно, [1, c. 38]. Прямые аффинного пространства являются прямыми пространства-времени Галилея , плоскости пространства являются плоскостями в .

1.2. Квадратичные формы галилеевой поверхности

Поверхность в пространстве-времени Галилея описывается векторной функцией

= , . (2)

Поверхность называется регулярной класса , если функция трижды дифференцируема, векторы неколлинеарны. Имеем:

, .

Первая квадратичная форма поверхности (2) такова

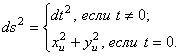(3)

Вид первой квадратичной формы поверхности такой же, как и галилеевой нормы векторов (1). Введено обозначение

, (4)

функция называется метрической функцией поверхности, [1, c. 73]. На ее основе вычисляются расстояния на поверхности, площади областей поверхности. Единичным вектором нормали поверхности (2) является

,

это евклидов вектор, перпендикулярный линиям поверхности . Вторая квадратичная форма поверхности (2) есть

, , , ; (5)

или в компонентах векторов:

, , . (6)

1.2. Аналог теоремы Петерсона-Бонне в симметричном задании поверхности

По формулам (4), (6) в [2] составлена система дифференциальных уравнений с частными производными

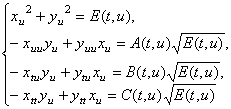(7)

и доказана основная теорема теории галилеевых поверхностей, аналогичная теореме Петерсона-Бонне евклидовой теории поверхностей.

1. ОСНОВНАЯ ТЕОРЕМА. Пусть на области евклидовой плоскости заданы функции класса

, (8)

Действительные функции класса на области , являющиеся решением системы дифференциальных уравнений с частными производными (7), определяют в галилеевом пространстве регулярную поверхность = , коэффициенты галилеевых квадратичных форм которой совпадают с заданными функциями (8). Начальные условия , , , , , определяют единственную поверхность, проходящую через точку и имеющую векторы касательных , .

См. также [3]. Схема отыскания функции по заданным функциям (7) такова. По виду первого уравнения системы (7) вводятся обозначения

, , (9)

функцию предстоит найти. Дифференцируем функции (9):

, ,

, .

Первые два равенства и второе уравнение системы (7) дают . Последние два равенства и третье уравнение системы (7) дают . Функция есть решение уравнения с полным дифференциалом

.

Интегрируем функции (9) по параметру , постоянными интегрирования являются функции параметра :

, . (10)

Дифференцируя дважды функции (10) по параметру и воспользовавшись четвертым уравнением системы (7), отыскиваем функции . В результате становятся известными функции . Поверхность (2) определяется функциями (8).

1.3 Аналог теоремы Петерсона-Бонне в явном задании поверхности

Условия регулярности поверхности (2) позволяют функцию, задающую поверхность, записать в виде

= . (11)

Это явное задание произвольной регулярной поверхности пространства-времени Галилея , функция (11) несимметрична относительно компонент, она выделяет третью компоненту координатного задания поверхности. Находим:

, , , , .

Вычислив , имеем:

, . (12)

В рассматриваемых условиях не видно, как коэффициент второй квадратичной формы поверхности может быть выражен через метрическую функцию (коэффициент первой квадратичной формы поверхности) и ее производные. Но в этих условиях система дифференциальных уравнений с частными производными (7) сводится к следующей системе дифференциальных уравнений с частными производными

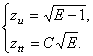(13)

Основная теорема теории галилеевых поверхностей принимает вид

2. ТЕОРЕМА. Если задан коэффициент первой квадратичной формы поверхности пространства-времени Галилея и коэффициент второй квадратичной формы

, (14)

то компонента функции (11), описывающая явно регулярную галилееву поверхность, является решением системы дифференциальных уравнений с частными производными (13). Начальные условия как в теореме 1 выделяют единственную поверхность.

В [4] для явно заданной поверхности в систему уравнений (13) включено лишнее уравнение. В рассматриваемом виде теорема сформулирована в [6]. Схема отыскания функции такова. По первому уравнению системы (13) имеем

.

Функция отыскивается по второму уравнению системы (13). Получаем .

2. Свойства поверхности, зависящие от ее метрической функции

2.1. Выражение коэффициентов второй квадратичной формы поверхности

через коэффициент первой квадратичной формы

Для регулярной поверхности евклидова пространства установлено, что коэффици-

енты второй квадратичной формы поверхности выражаются через коэффициенты первой квадратичной формы и их производные, [5]. Обратимся к галилеевым поверхностям.

3. ТЕОРЕМА. В случае, если

или , (15)

коэффициенты второй квадратичной формы регулярной поверхности пространства-времени Галилея выражаются через метрическую функцию и ее производные.

# Выше, в (12) имеются необходимые формулы для независимо от дополнительных условий (15). Полная кривизна гелилеевой поверхности по [1, c. 81] есть:

.

Воспользуемся (12):

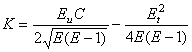
. (16)

Выполняется аналог формулы Гаусса, [1, c. 94]:

. (17)

По виду формулы должны соблюдаться условия (15). Сравнивая (16) и (17), находим

. # (18)

В [1] не отмечены очевидные условия (15) для (17). Если или , то и, по (17), , что неверно. Например, для поверхностей

имеем: , , , и , а по (17) значение нулевое. Если , то является плоскостью, для нее . Итак, не для всякой поверхности пространства-времени Галилея коэффициенты ее второй квадратичной формы выражаются через коэффициент первой квадратичной формы.

4. ТЕОРЕМА. Если задана функция и выполняются (15), то поверхность (11) пространства-времени Галилея определяется однозначно, с точностью до положения в пространстве:

,

слагаемое отыскивается, согласно (18), из условия

.

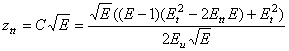# Утверждение следует из теоремы 3. #

2.2. О внутренней геометрии галилеевых поверхностей

Внутренняя геометрия поверхности основана на свойствах ее первой квадратичной формы. Так как для евклидовой поверхности коэффициенты второй квадратичной формы выражены через коэффициенты первой квадратичной формы, [5], то ее внутренняя геометрия изучает свойства изгибаемости поверхности. Выше, в п. 2.1, установлено, что не для всякой регулярной поверхности пространства-времени Галилея коэффициенты второй квадратичной формы выражаются через коэффициент первой квадратичной формы. В этом принципиальной отличие евклидовой геометрии поверхностей от галилеевой геометрии поверхностей.

К внутренней геометрии поверхности относятся символы Кристоффеля. Для поверхности (2) они вычислены в [1]:

, = , = , .

отметим некоторые свойства поверхностей из [7].

5. ТЕОРЕМА. [7, теорема 2] Если заданы дифференцируемые функции на области евклидовой плоскости, то метрическая функция поверхности (2) определяется как решение системы дифференциальных уравнений с частными производными

= 0.

Масштаб измерения времени в событиях на поверхности определяется символом .

6. ТЕОРЕМА. [7, теорема 4] Поверхность пространства-времени Галилея однозначно определяется заданными символами Кристоффеля, если все коэффициенты квадратичных форм поверхности зависят от временного параметра и в случае если , , .

7. ТЕОРЕМА. [7, теорема 5] Всякая поверхность, все коэффициенты квадратичных форм которой зависят только от временного параметра , неизгибаема.

В [7] приведены некоторые классы изгибаемых поверхностей.

Литература

1. Долгарев А.И. Классические методы в дифференциальной геометрии одулярных пространств. Монография. – Пенза: ИИЦ ПГУ, 2005.- 306с.
2. Долгарев И.А. Нахождение поверхности в 3-мерном пространстве Галилея по ее квадратичным формам.// Известия высш. учебных завед. Поволжский регион. Сер. Естественные науки, Пенза: ИИЦ ПГУ, 2006, № 5(26). – С. 51 – 60.
3. Долгарев И.А. Системы дифференциальных уравнений в частных производных для поверхностей пространства Галилея.// Дис. … канд. физ.-мат. наук. – Пенза: ПГУ, 2007, - 120 с.

4. Долгарев И.А. Галилеевы квадратичные формы евклидовой поверхности.// Метрическая геометрия поверхностей и многогранников – Междунар конф памяти Ефимова Н.В., МГУ, Москва, 18 – 21 авг. 1210. Сборник тезисов. – Москва: МАКС Пресс 2010. С. 24 – 25.

5. Долгарев А.И. Новый вид основной теоремы Гаусса в евклидовой теории поверхностей. //Materiali IX mezinarodni vedecko-praktika conference «Dni vedi – 2013» - Dil 32. Matematika. Vystavba a archtektura: Praga. Publiching House “Education and Skience”. s.r.o. – 112. С. 55 – 60.

6. Долгарев И.А. и Долгарев А.И. Галилеевы идеи в курсе евклидовой дифференциальной геометрии.// Вестник Красноярского педуниверситета им. В.П. Астафьева, 2013 № 1(23), Красноярск, 2013, С. 232 – 235.
7. Долгарев И.А. Поверхности пространства-времени Галилея по символам Кристоффеля.//Известия высших учебных заведений. Поволжский регион. Физико-математические науки, Пенза: ИИЦ ПГУ – 2008 , № 2(6), С. 39 – 50.