Mathematics / 4. Applied Mathematics /
O.F. Ryaboshtan,
Ph.D. A.M. Milenin, Ph.D. S.M. Skofenko
Kharkov National
Technical University of Agriculture after P. Vasilenko
Algorithm for calculating the surface
bypass gas turbine blade
Consider the method of preparation
of the equation arc flat bypass incident with points ![]() and
and ![]() calculated using
the formula
calculated using
the formula
![]() . (1)
. (1)
Its derivatives
![]() , (2)
, (2)
![]() . (3)
. (3)
Let the function ![]() has the form
has the form
![]() ,
(4)
,
(4)
where ![]() ,
, ![]() ,
, ![]() - Basic linearly
independent functions
- Basic linearly
independent functions
![]() ,
, ![]() ,
, ![]() - numerical coefficients.
- numerical coefficients.
Then
![]() , (5)
, (5)
![]() . (6)
. (6)
Equations (1) ... (3) with (4) ...
(6) ![]() ,
, ![]() ,
, ![]() ,
, ![]() , constitute a system,
a relatively linear
, constitute a system,
a relatively linear ![]() ,
, ![]() ,
, ![]()
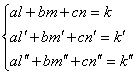 (7)
(7)
 (8)
(8)
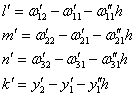 (9)
(9)
![]() (10)
(10)
![]() ,
, ![]() , …,
, …, ![]() - values of the functions
- values of the functions ![]() ,
, ![]() ,
, ![]() and their derivatives at
and their derivatives at ![]() ,,
,,
![]() ,
, ![]() , …,
, …, ![]() - the values of the functions at the same
- the values of the functions at the same ![]() .
.
Calculation algorithm:
1. choosing a set of basis functions ![]() ,
, ![]() ,
, ![]() ;
;
2. define their derivatives ![]() ,
, ![]() , …,
, …, ![]() ;
;
3. find the values of functions and their derivatives at
the points ![]() ,
, ![]() ;
;
4. we expect the coefficients ![]() ,
, ![]() ,
, ![]() ,
, ![]() , …,
, …, ![]() ,
, ![]() ,
, ![]() ,
, ![]() according to (8), (9) and (10);
according to (8), (9) and (10);
5. find the determinants of
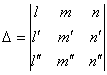
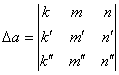
(11)
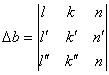
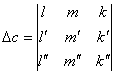
6. determine the values of the
coefficients
![]() ;
; ![]() ,
, ![]() .
(12)
.
(12)
7. define a function ![]() and its derivatives (4), (5), (6) with (12);
and its derivatives (4), (5), (6) with (12);
8. we find the values ![]() ,
, ![]() ,
, ![]() at
at ![]() ;
;
9. the results of points 7 and 8 substitute in equation
(1).
In the case of an algebraic
polynomial
 (13)
(13)
1-9 points decision algorithm of
calculation leads to an equation of bypass gas turbine blade on the site ![]() as:
as:
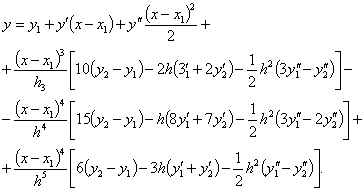 (14)
(14)
The calculation is based interface
surface area gas turbine blades put equation (14), but the method of
calculation set out has the disadvantage that the result of the determination
of derivatives at the points on the resulting equation is an accumulation of
errors, resulting in the calculation process can be unstable. To avoid this, you need to solve the differential
equation for determining ![]() and
and ![]() at the first point and assign them such that the error
tended to be low. Such a process can be organized.
at the first point and assign them such that the error
tended to be low. Such a process can be organized.