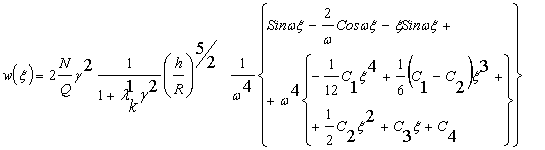Божанов Е.Т., Ибраймкулов А.М., Сатыбалдиев О.С.,

Нуралем Н., Касымбекова М.Т.

КазНТУ им. К.И.Сатпаева, г.Алматы, Казахстан

Аналитико расчетная модель изгиба трубчатой конструкции из эластомера, с переменными параметрами, когда форма поперечного сечения конусоидального типа

1. В работе разработана аналитико- расчетная модель трубчатой конструкции из слойстого элостомера.Вопросы влияния возмущения заполнителя на динамику каркаса изучены в зависимости вида дифференциального уравнения изогнутой оси с учетом внутренного трения поперечного сечения за пределом упругости.

Вид поперечного сечения изогнутой оси

,

Рассмотрено в предположении, что на краю торцевой зоны контакта терпит разрыв перерезывающая сила и приращение изгибающего момента определяется по формуле

,

Где - безразмерный параметр в продольном направлении. Уравнения движения разделены к системе обыкновенных дифференциальных уравнений относительно переменной и времени .

Далее получено аналитическое решение для функции прогиба методом суперпозиции изгибов в случае возмущения памяти пластиков. При выборе граничных условий на торцах не рассматривается критическая скорость движения и инерция деформация релаксации. В связи с чем на величину активной критической нагрузки не оказывает существенное влияние начальные условия по времени.

Численные результаты работы показывают: что выводы из 9(девяти) рекомендаций призваны обеспечить надежность технологического процесса модели изгиба конструкции из слойстых эластомеров.

2.Дифференциальное уравнение для численного расчета является одним из вариантов решения дифференциального уравнения:

,

- новая константа материала из континуума Коссера, Д- цилиндрическая жесткость трубчатой конструкции.

Пусть длина конструкции почти не влияет на величину критического импульса внешней критической динамической нагрузки, которая существенным образом зависит от выбора функции

плотности тента в поперечной сечении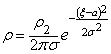

; ;
Здесь математическое ожидание, дисперсия, средне квадратическое отклонение на отрезке. Схема функционирования физико-технических и химико-технологических характеристик трубчатых конструкции приведена в работах [1]-[6].

Уравнение движения заполнителя трубчатой конструкции возьмем в виде [3]-[6]

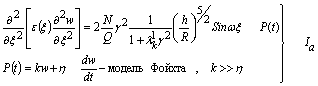
Если для аналитического расчета предположим из постановки задачи

то система имеет вид:

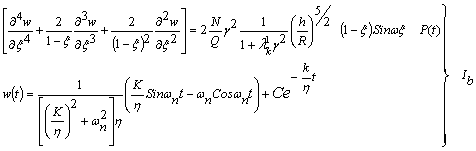
Первое уравнение системы () перепишем в виде

(1)

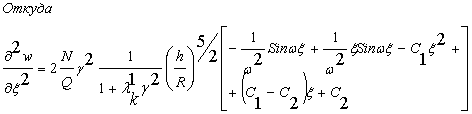
Следовательно

(2)

Подставля (2) в граничные условия :

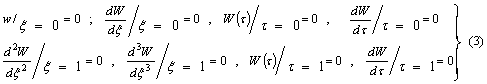где - варияция амплитуд, являющейся функциями времени при имеем:

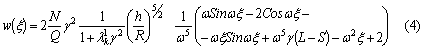
Если эту же систему уравнения () решим аналогично на отрезке [0,3 ; 0,6] при граничных условиях

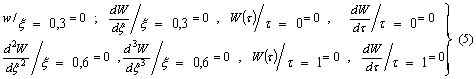то с учетом условий

получим:

Здесь (N,Q) – анизотропные характеристики приведенного слоя поперечного сечения слоистого эластомера , - число полуволн в поперечном направлении, число полуволн в продольном направлении, определяется из граничных условий на поверхности и .

-по нелинейным деформационным процессам, толщина, длина, внутренний

радиус трубчатой конструкции

изменение изгибающего момента за пределом упругости.

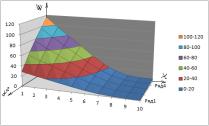
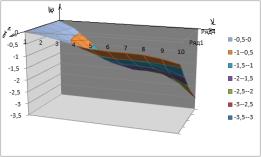
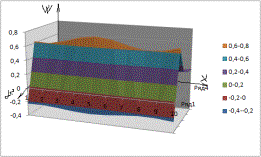
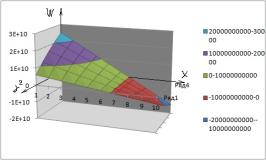
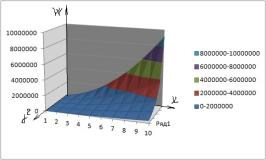
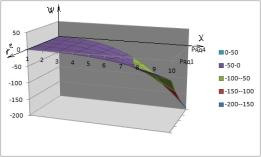
.На графиках №1- №6 приведены возмущение заполнителя, когда форма поперечного сечения конусойдальная в зависимости функции:

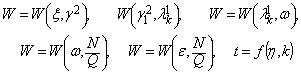
из формул (1) второе уравнение системы и (5) при следующих данных:

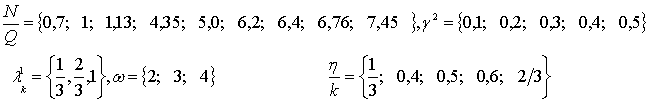
На графиках 1-9 приведены выпучивание трубчатой слойствой конструкции конусойдального сечения.

График 1 по М.Л. Био	График 3 по М.Л. Гузю
График 2 по первому упрощению В.В.	График 4 по А.М. Лейбензону Новожилову
График 5 по А.С. Био	График 8 по Гузю
График 6 по Био	График 9 по Лейбензону
График 7 по Новожилову

Исходя из естественно – физических, физико-технических и химико-технологических прцессов эластомера и из аналитико – расчетной модели сделаем следуюшие выводы.

Выводы из анализа призванные обеспечить надежность технологического процесса

1) Предварительное нагружение поперечного сечения внешним активным критическим давлением уменышает коэффицент динамичности, а внутренние нагружение критической силой наоборот повышает коэффициент динамичности;

2) В статике граничные условия оказывают существенное влияние на величину активной критической нагрузки, а в динамике граничные условия роли не играют из-за начальных условий:

`

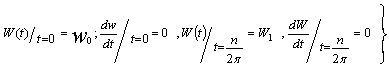
где - прогиб, соответствующий критическому давлению

(3) За критическое время практически можно принимать любое соответствующее промежутку выпучивание где наблюдается разное возрастание прогиба. Здесь точка перегиба кривой ,

4) С увеличением показателя коэффициент динамичности растет. При этом внешние критические активные и внутренние критические реактивные силы на участке могут работать в противоположных направлениях, исключая промежуток времени

5) При предложении для случая

предполагаемая модель не позволяет найти давление в классе непрерывных функции , так как на краю зоны контакта терпит разрыв перерезывающая сила, которая зависит от изменениий приращений изгибающего момента. Следовательно, можно ставить дополнительный произвол

для аналитико-графического расчета.

6) При выборе граничных условий (2) не рассматривается критическая скорость движения тента с массой , где инерция катающейся части нагрузки равна нулю:

7) Плотность материала поперечного сечения как переменная величина уменьшается в сторону большого основания гидростатического давления для (шапки или подошвы) систем конструкции согласно нормальному закону распределения плотностей непрерывных случайных величин на отрезке по формуле

8) Существенное влияние на величину прогиба оказывает анизотропия материала (N,Q) и степени податливости подошвы (возможно шапки) систем конструкции на поперечный сдаиг на отрезке , проницаемости и уплотнение заполнителя. (график 4-5)

9) Значение прогиба по теории М.А.Био отличается от значения прогиба по теории В.В.Новожилова от 6% до 8%; а от смешанного подхода А.Ю.Ишлинского от 2% до 26%; в зависимости от толщины конструкции если то эти отличия составляют 2% до 40% (график1-2)

Если рассматреть резино - металлические трубчатые конструкции с несколькими юбками, то поперечное сечение можно представить в виде конусоидальной формы при критической нагрузке, распределенной в ряд Фурье вдоль параллели

Резонанс может наступить по временным координатам в условии

и с амплитудой

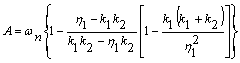
Условие резонанса

Будет когда резонанс наступает одновременно только от вида активного внешнего и реактивного внутреннего критического нагружения и пульсации опор.

Список литературы

1.Божанов Е.Т., Ержанов Ж.С. «Исследование проблем устойчивости упругих тел, гибких пластин и оболочек и их приложения», Издательство «Қазақстан жоғарғы мектебі», монография, Алматы, 2001г., 324 с.

2. Рахимбекова З.М., “нелинейные стержневые системы за пределом упругости”, Алматы, 2002г., 218 с.

3. Победря Б.Е. “ Проблемы прочности композиционных материалов ”, киев, «Знание», 1986г. , 19 с.

4. Божанов Е.Т., Ибраимкулов А.М., Жаканова А., Дмитриева Н. «Исследование устойчивости и выпучивания композитов из чередующихся двух «бутербродов» под действием критической силы по теориям М.А.Био, В.В.Новожилова, А.Н.Гузя», труды международной научно-практической конференции «Иформационные и телекоммуникационные технологии: оброзование, наука, практика», Алматы, 2012г.,том II.

5. Божанов Е.Т. , Ибраимкулов А.М. , Дмитриева Н. , Жаканова А. «Выпучивание композитов в зависимости от предельной гибкости поперечного сечения по теориям Л.С.Лейбензона, А.Ю.Ишлинского», труды международной научно-практической конференции «Информационные и телекоммуникационные технологии: образование, наука,практика» Алматы, 2012г. , том II.

6. Кильчевский Н.А. “теория не стационарных динамических процессов в оболочках” прикладная математика, 1968, том 4, Вып 8.