А.И. Долгарев

ГРУППЫ СТУПЕНИ 3 ПРОСТОГО ПЕРИОДА.

4. ЗАВИСИМОСТЬ ПЕРИОДА ГРУППЫ ОТ СТУПЕНИ НИЛЬПОТЕНТНОСТИ. ДЕЛИМОСТЬ (ПОЛНОТА) ГРУППЫ

Работа относится к циклу статей о группах ступени 3 периода , является продолжением [1]. группы нильпотентны, представляются матрицами из , где поле Галуа. Группы ступени 2 описаны в [2], в [1] начато изучение групп ступени 3. Групповую операцию считаем сложением. Нильпотентная группа, на которой определена внешняя операция умножения ее элементов на скаляры из некоторого кольца (поля), называется сибсоном. Элементы сибсона называются сибсами. Скаляры обозначаем , сибсы обозначаем ; нулевой сибс – . Сибсон относится к одулям Л.В. Сабинина, является обобщением линейного пространства.

Выделяются минимальные группы каждой ступени, они порождаются наименьшим числом элементов. Минимальная группа ступени 2 порождается двумя элементами: =, ее порядок равен , коммутант порождается коммутатором = совпадает с центром и подгруппой Фраттини . Всякая конечная группа простого периода ступени 2 получена из групп , [2].

Нильпотентные группы представляются группами кортежей элементов поля . Сибсон наименьшей размерности 3 на группе в [2] определен операциями

, (1)

. (2)

Нулевой сибс есть ; если = , то . Имеем: , , . Изоморфное соответствие между и таково

.

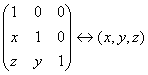Всякая конечная нильпотентная группа изоморфно вкладывается в унитреугольную группу , [3, c.157], кольцо целых чисел. Нильпотентная группа ступени изоморфна подгруппе в , , поле. Ступень нильпотентности группы равна , [3, c.145]. Выполняется соотношение: .

Минимальная группа ступени 3 изоморфна группе и группе кортежей с операцией

= , (3)

[1, теорема 2]. Имеется изоморфное соответствие

.

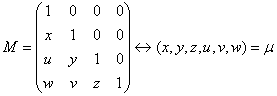При этом, , = . Сибсон

определен на группе внешней операцией:

=

, , (4)

[1, теорема 3]. Группа и сибсон порождается тремя элементами. Подгруппа Фраттини совпадает с коммутантом , абелева, имеет порядок ; центр лежит в коммутанте, , его порядок , [1, теорема 6].

Существует минимальная группа ступени 3 порожденная 4 элементами. По теореме 12 из [1], группа с коммутантом порядка задается операцией сложения

=.(5)

Сибсон определен на = внешней операцией

=

, , (6)

Коммутанты групп и имеют наименьший порядок , = , порядок центра равен , [1, теорема 14]. Группа изоморфна подгруппе в , группа изоморфна подгруппе в , [1].

1. Леммы о минимальных группах

1. ЛЕММА. 3-порожденная группа является минимальной нильпотентной группой ступени .

# Всякая нильпотентная группа ступени вкладывается в унитреугольную группу , [3, c. 157]. 3-порожденная группа вкладывается в 3-порожденную группу и изоморфна . Значит, является минимальной группой . #

2. ЛЕММА. Нильпотентная ступени 3 группа , , имеет хотя бы одну подгруппу ступени 3.

# Пусть всякая 3-порожденная подгруппа группы нильпотентна ступени 2. Через обозначим порождающие элементы группы . Рассмотрим 3-порожденную подгруппу = в , все не превосходят . Для группы ступени 2: . Следовательно, для любых , и в нижнем центральном ряду группы коммутант лежит в центре , см. [3, c. 135], т.е. длина ряда централов на 1 меньше и ступень группы равна 2. Таким образом, сделанное предположение противоречит условию и лемма выполняется. #

3. ЛЕММА. Группа = периода с коммутантом порядка либо является прямой суммой , где циклическая порядка , либо содержит коммутаторы , , ==, т.е. является группой .

# По лемме 2, содержит подгруппу , пусть = . Конечная нильпотентная группа обладает нетривиальным центром, [3, c. 154]. Обозначим: . Если и , то , а тогда =+. Если ,

то , . Обозначим . Если ступень нильпотентности подгруппы равна 3, то эта подгруппа есть и =

=. В подгруппе ступени 3 коммутаторы и , согласно [2], лежат в различных циклических и имеет порядок, больший, чем . Поэтому невозможно =, следовательно, , т.е. . По свойствам групп ступени 2 с коммутантом порядка , [1], можно в выбрать порождающий , чтобы . В этом случае =. #

2. Зависимость периода группы от ступени ее нильпотентности

2.1. О группах ступени 2

4. ТЕОРЕМА. Период группы ступени 2 больше 2.

# Нильпотентная некоммутативная 2-порожденная группа кортежей задается операцией (1), см. [1]. Пусть поле Галуа из двух элементов, в имеется тройка . Находим сумму . Рассматриваемая тройка, как элемент группы, имеет порядок 4, отличный от 2. Во всякой некоммутативной 2-группе ступени 2 имеется 2-порожденная подгруппа , , всякий ее элемент записывается в виде , где . Для выполняется соотношение =. Порядок элемента отличен от 2. Группа не может иметь период 2. #

Если , то по (1), и группа имеет период . Доказанная теорема дополняет работу [2] в описании 2-ступенно нильпотентных групп, где изучаются группы нечетного простого периода. На основании теоремы 4 справедлива

5. ТЕОРЕМА. Группы периода 2 могут быть только абелевыми. #

Вместе с тем выполняется

6. ТЕОРЕМА. Если группа имеет период 3, то это либо элементарная абелева группа, либо группа ступени 2. #

Эта теорема, характеризующая группы ступени 2, следует из теоремы 7 следующего п. 2.2 о группах периода 3.

2.2. О группах ступени 3

7. ТЕОРЕМА. Период группы ступени 3 больше 3.

# На группе определены операции (3) и (4). Если поле Галуа из двух элементов, то . Порядок элемента больше 2. По лемме 2, группа ступени 3 содержит 3-порожденную подгруппу ступени 3, а такая подгруппа имеет элементы порядка больше 2.

Пусть . В (7) положим . Положим: . Имеем:

= .

При : . Порядок этого элемента больше 3. Всякая 3-порожденная подгруппа группы ступени 3 содержит элементы порядков, отличных от 3. #

При в (7) получаем , значит, период 3-ступенной группы равен при . Для групп периода 5 выполняется

8. ТЕОРЕМА. Если группа имеет период 5, то она либо элементарная абелева, либо группа ступени 2, либо группа ступени 3. #

2.3. О группах большей ступени

Теоремы, доказанные выше, позволяют предположить, что выполняется следующая

ГИПОТЕЗА. Период группы ступени больше . Группа периода есть группа, ступень которой превосходит .

3. Делимость (полнота) групп

3.1. Делимость конечной группы простого периода ступени 3

с коммутантом наименьшего порядка

В [1, теорема 4] доказана полнота конечных групп простого нечетного периода ступени 2. Пусть группа имеет простой период и , поле состоит из элементов. Группа периода называется делимой, если для любого и любого существует единственный элемент , что . На рассматриваемых группах в [1] определены сибсоны посредством задания внешних операций умножения элементов групп на элементы поля Галуа . Тем самым, для всякого и всякого существует в элемент . Делимость группы периода означает обратимость этого утверждения.

9. ТЕОРЕМА. Всякая конечная группа простого периода , на которой определен сибсон, является полной.

# Пусть на группе периода определена операция умножения элементов группы на элементы поля Галуа , состоящего из элементов. Для всякого и всякого в группе существует единственный элемент , обозначим его . В поле всякий ненулевой элемент обратим, т.е. существует , что . Умножим равенство на : , тем самым элемент определяется однозначно. #

3.2. Полнота и неполнота некоторых групп

10. ТЕОРЕМА. Если группа полна, тогда для и .

# Символ означает, что рассматривается множество элементов для всех и для . Полнота группы означает, что всякий элемент является кратным некоторого единственного элемента группы, поэтому совпадает с . #

Пусть группа ступени 2, состоящая из кортежей длины элементов поля Галуа характеристики 2. Согласно п. 3.1, группа содержит элементы , что . Вместе с тем, . Группа не является группой периода 2, теорема 4, группа не полна. Если группа ступени 3 и характеристика поля есть 2 или 3, то , по пп. 2.1 и 2.2, группа содержит элемент , что , соответственно . Группа не полна. Справедливы следующие включения: , соответственно .

Литература

1. Долгарев А.И. Группы ступени 3. 1. Конечные минимальные нильпотентные группы простого периода ступени 3. Материали за IX международна научна практична конференция «Новини на научния прогресс – 2013» . Том 9. Технологии Съвременни технологии на информации. Математика. София. «Бял ГРАД-БГ» ООД, 2013. С. 50 – 59.
2. Долгарев А.И. Описание конечных нильпотентных групп степени 2 простого нечетного периода.// Известия вузов. Математика. – 2008. № 12. – С. 17 – 27.
3. Каргаполов М.И., Мерзляков Ю.И. Основы теории групп. 3-е изд. – М.: Наука, 1982. – 288с.