Математика/5. Математическое моделирование
Baimankulov A.
Kostanay State
University named after A.Baitursynov,
Kazakhstan.
Identification of the
diffusion coefficient
Problem is studied in
the field of ![]()
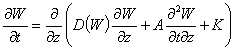 , (1)
, (1)
![]() ,
, ![]() (2)
(2)
![]() (3)
(3)
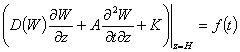 , (4)
, (4)
where
 . (5)
. (5)
Moisture is given on soil surface to
determine the ![]()
![]() . (6)
. (6)
We show
that the diffusion coefficient ![]() can be determined in an iterative manner..
Let
can be determined in an iterative manner..
Let ![]() and
and ![]() be two successive
approximations coefficient
be two successive
approximations coefficient![]() . Corresponding
solution of problem (1) - (5) is denoted by
. Corresponding
solution of problem (1) - (5) is denoted by ![]() and
and ![]() .Then for the
difference
.Then for the
difference ![]() we obtain the problem:
we obtain the problem:
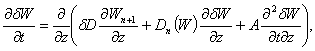 (7)
(7)
![]() . (8)
. (8)
 . (9)
. (9)
Multiplying
(7) by ![]() integrating over all points of
the domain
integrating over all points of
the domain ![]() and assuming that,
and assuming that, ![]() ,
, ![]() we obtain
we obtain
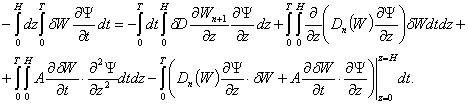
Performing
a transformation on the right side and in view of our assumptions, we have
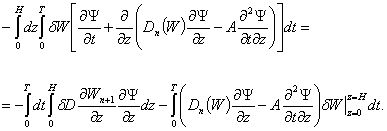 (10)
(10)
Assuming that
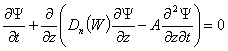 ,
, 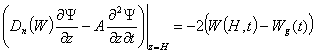
we obtain the
formula from (10)
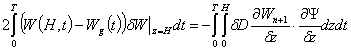 . (11)
. (11)
By setting
![]() following approximation
following approximation ![]() , determining the
condition of monotonicity of the functional
, determining the
condition of monotonicity of the functional
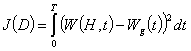
can be expressed by
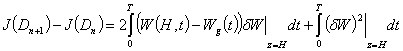 ,
,
where
![]()
Using formula (11) we
deduce that
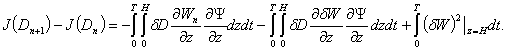
Movement of ![]() select by the formula
select by the formula
![]() .
.
where ![]() - sufficiently
small number.
- sufficiently
small number.
function
![]() , determined from
the solution of the adjoint problem
, determined from
the solution of the adjoint problem
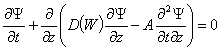 , (12)
, (12)
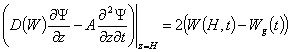 , (13)
, (13)
![]()
References
1.Нерпин С.В., Юзефович Г.И. О расчете
нестационарного движения влаги в почве// Доклады ВАСХНИЛ, № 6, 1966.
2.Юзефович Г.И., Янгарбер В.А.
Исследование нелинейного уравнения влагопереноса. // Л.: Колос. Сб. трудов по
агрофизике, вып. № 14, 1967.
3.Байманкулов А.Т. Определение
коэффициента капиллярной диффузии.// Материали за VIII международна научна практична конференция «Бъдещето
въпроси от света на науката -2012», т.36, 17-25 декември, 2012, София.