К.ф.-м.н.,
профессор Паршин А.В.
ВУНЦ ВВС «ВВА
имени профессора Н.Е. Жуковского и Ю.А. Гагарина»
(г. Воронеж), Россия
Средства для повышения эффективности проведения
автоматизированного практического занятия «Матричные и числовые
характеристики неориентированных графов»
В монографии [1] показано, что
использование компьютерных математических систем при проведении практических
занятий по математике приводит к значительной их интенсификации, что позволяет
повысить качество подготовки курсантов. Но наряду с этим разработка
компьютерных программ учебного назначения и их применение для интенсификации и
автоматизации практических занятий на наш взгляд также должна приводить к
повышению качества математического образования курсантов. Чтобы в этом
убедиться нами была выбрана тема прикладной математики «Основные понятия теории
графов». Этот раздел преподается на двух специальностях «Средства радиоэлектронной
борьбы» и «Информационная безопасность автоматизированных систем» на 5
факультете ВУНЦ ВВС «ВВА». По этой теме предусмотрено проведение 4 практических
занятий. Первое из них называется «Матричные и числовые характеристики
неориентированных графов» и включает в себя 2 учебных вопроса: 1) матричные
характеристики неориентированных графов; 2) числовые характеристики
неориентированных графов.
С целью интенсификации и автоматизации
этого занятия была разработана обучающая программа [2].
Разработанная
обучающая программа содержит в себе:
1)
теоретическую информацию об изучаемых алгоритмах;
2)
модуль тестирования, осуществляющий проведение входного контроля знаний и
умений курсантов по теме занятия с проставлением оценки;
3)
двадцать пять вариантов индивидуальных заданий, выполняемых на ПЭВМ в диалоговом
режиме с автоматизацией всех рутинных вычислений, отвлекающих внимание
обучаемых от освоения алгоритмов изучаемых методов.
4)
визуально-графическое сопровождение выполняемых заданий;
5)
контроль правильности выполняемых обучающимся действий с фиксацией количества
ошибок;
6)
сопутствующие сообщения о ходе выполнения работы;
7) отображение результатов по окончании работы с
проставлением оценки.
Достаточно большое количество вариантов
заданий (25 вариантов) позволяет осуществлять тренаж знаний и умений по теме
занятия.
Для реализации поставленной задачи
использовался язык Object Pascal в среде программирования
Delphi 7.
В качестве аппаратной среды используются
персональные компьютеры типа IBM PC.
Программное обеспечение
должно включать операционную систему Windows
версии не ниже 98.
В начале работы программы на
экране отображается главная форма (рисунок 1), которая содержит меню и
информацию о том, что пользователю нужно сначала зарегистрироваться, нажав на
пункт меню «Регистрация». Для того, чтобы узнать информацию о программе,
необходимо нажать на пункт меню «О программе». Для получения теоретической
справки нажимают на пункт меню «Теория». Для прохождения тестирования с целью
входного контроля знаний и умений нажимают на пункт меню «Тестирование». После
прохождения тестирования программа проставляет курсанту оценку. Для выхода из
программы нужно нажать пункт меню «Выход».
Рисунок 1 – Главная форма обучающей программы
После успешной регистрации
необходимо нажать на пункт меню «Теория». Появляется форма теоретической
справки.
После
нажатия на пункт меню «Тестирование» появляется форма (рис. 2).
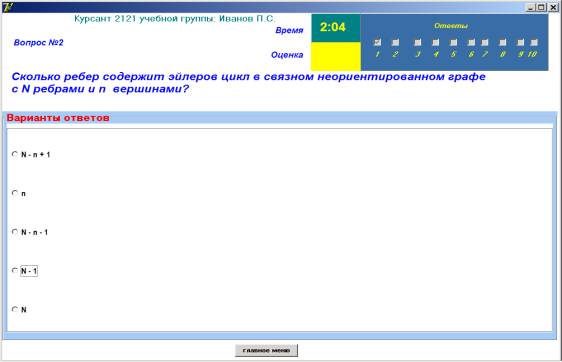
Рисунок 2 – Форма меню
«Тестирование»
Для выполнения
индивидуального задания необходимо нажать на пункт меню «Задание». Появляется
форма (рис. 3), на которой дается формулировка варианта индивидуального
задания.
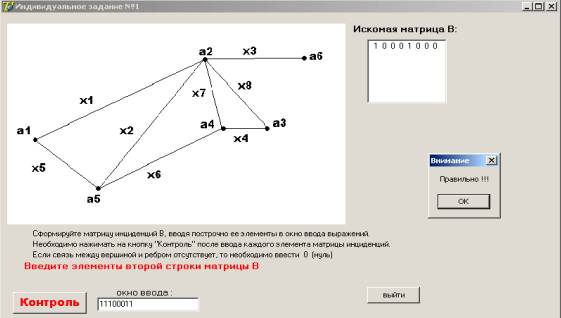
Рисунок 3 –Выполнение варианта индивидуального задания
Для доказательства того, что применение
разработанной обучающей программы приведет к повышению эффективности проведения
соответствующего практического занятия, был проведен педагогический
эксперимент, который осуществлялся в 3 этапа.
На
первом начальном этапе экспертом
(одним из авторов) был проведен сравнительный анализ затрат учебного времени на
решение комплекта из 20 задач (примерно в 2-3 раза больше количество задач,
прорешиваемых на занятии обычным образом) двумя способами: вручную и с
использованием разработанной программы.
Комплект состоял из следующих учебных
задач:
Первый учебный вопрос
Задача 1. Для неографа, изображенного на рис. 4, найти матрицу
смежности A
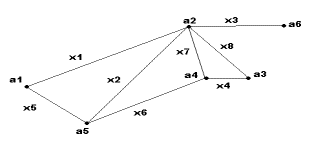
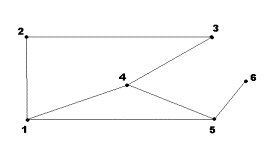
Рисунок 4 Рисунок 5
Задача 2. Для неографа, изображенного на рис. 4, найти матрицу
инциденций B.
Задача 3. Для неографа, изображенного на рис. 5, найти матрицу
расстояний P
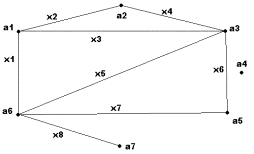
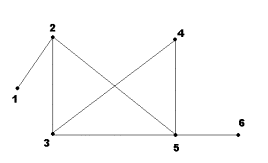
Рисунок 6 Рисунок 7
Задача 4. Для неографа, изображенного на рис. 6, найти матрицу
смежности A
Задача 5. Для неографа, изображенного на рис. 6, найти матрицу
инциденций B.
Задача 6. Для неографа, изображенного на рис. 7, найти матрицу
расстояний P
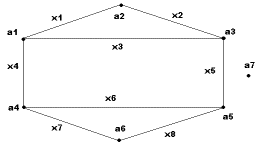
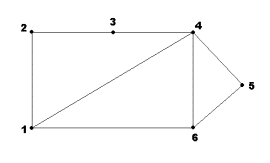
Рисунок 8 Рисунок 9
Задача 7. Для неографа, изображенного на рис. 8, найти матрицу
смежности A
Задача 8. Для неографа, изображенного на рис. 8, найти
матрицу инциденций B.
Задача 9. Для неографа, изображенного на рис. 9, найти матрицу
расстояний P
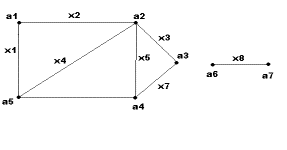
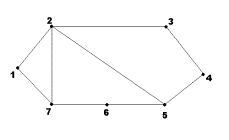
Рисунок
10
Рисунок 11
Задача 10. Для неографа, изображенного на рис. 10, найти
матрицу смежности A
Задача 11. Для неографа, изображенного на рис. 10, найти
матрицу инциденций B.
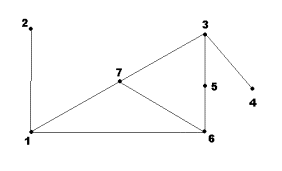
Задача 12. Для неографа, изображенного на рис. 11, найти
матрицу расстояний P
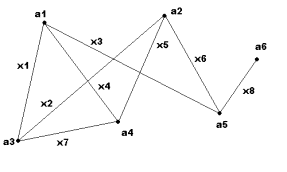
Рисунок
12
Рисунок 13
Задача 13. Для неографа, изображенного на рис. 12, найти
матрицу смежности A
Задача 14. Для неографа, изображенного на рис. 12, найти
матрицу инциденций B.
Задача 15. Для неографа, изображенного на рис. 13, найти
матрицу расстояний P
Второй учебный вопрос
Задача 16.
Для неографа, изображенного на рис. 5, найти следующие числовые характеристики:
эксцентриситет е
вершины 3;
радиус графа r(G);
диаметр графа d(G);
множество центральных вершин E(Ц);
множество периферийных вершин E(П)
Задача 17. Для неографа, изображенного на рис. 7, найти: е
, r(G), d(G), E(Ц), E(П)
Задача 18. Для неографа, изображенного на рис. 9, найти: е
, r(G), d(G), E(Ц), E(П)
Задача 19. Для неографа, изображенного на рис. 11, найти: е
, r(G), d(G), E(Ц), E(П)
Задача 20. Для неографа, изображенного на рис. 13, найти: е
, r(G), d(G), E(Ц), E(П)
Приведем решения экспертом следующих 4
показных задач комплекта двумя способами: вручную и с использованием обучающей
программы. В конце приведенных примеров указывается время, затраченное
экспертом на решение каждой из показных задач.
Решение
задачи 1 вручную. Так как на данном
графе отсутствует петля 
, то 
. Поскольку на нем имеется ребро 
, соединяющее вершины 
и 
, то 
. В связи с отсутствием ребра, соединяющего вершины 
и 
имеем 
. Аналогично находим остальные элементы 
матрицы смежности 
. В результате получаем
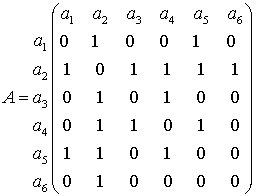(8 мин).
Решение
задачи 1 с использованием обучающей программы (3,5 мин).
Решение
задачи 2 вручную. Так как ребро 
, данного неографа инцидентно вершинам 
и 
, то 
, а остальные элементы первого столбца равны нулю, т.е. 
. Аналогично находим элементы других столбцов матрицы инциденций
. В результате получаем
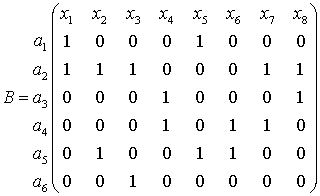(7 мин).
Решение
задачи 2 с использованием обучающей программы (3 мин).
Решение
задачи 3 вручную. Очевидно, что 
. Так как кратчайший (1,2)– маршрут состоит из одного ребра,
то 
. Поскольку кратчайший (1,3)– маршрут содержит два ребра, то 
. Аналогично находим остальные элементы 
матрицы расстояний 
. В результате получаем
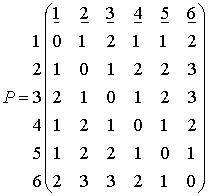(9 мин).
Решение
задачи 3 с использованием обучающей программы (3,9 мин).
Решение
задачи 16 вручную. Как следует из
теории, для решения данной задачи нужно сначала найти матрицу расстояний 
для данного графа.
Она найдена в задаче 3.
Из определения следует, что эксцентриситет 
–й вершины данного графа равен наибольшему из чисел, стоящих
в 
–й строке его матрицы расстояний. Поэтому 
. Далее находим радиус и диаметр графа:
,
.
Поскольку эксцентриситеты 1,4, и 5 вершин совпадают с
радиусом графа, то множество центральных вершин равно 
. Так как эксцентриситеты 2,3 и 6 равны диаметру графа, то
множество периферийных вершин равно 
.
(2 мин)
Решение
задачи 16 с использованием обучающей программы (0,8 мин).
Результаты первого начального этапа эксперимента
приведены в табл. 1.
Таблица 1 – Время, затраченное экспертом на решение
всего комплекта задач
|
№ задачи |
|
|
|
1 |
8.0 |
3.5 |
|
2 |
7.0 |
3.0 |
|
3 |
9.0 |
3.9 |
|
4 |
8.3 |
2.9 |
|
5 |
7.5 |
3.1 |
|
6 |
9.5 |
3.5 |
|
7 |
9.0 |
3.7 |
|
8 |
7.2 |
3.1 |
|
9 |
9.9 |
3.8 |
|
10 |
8.1 |
3.4 |
|
11 |
7.1 |
3.0 |
|
12 |
9.2 |
3.9 |
|
13 |
9.3 |
3.5 |
|
14 |
9.2 |
3.1 |
|
15 |
10.3 |
3.9 |
|
16 |
2.0 |
0.8 |
|
17 |
2.1 |
0.8 |
|
18 |
2.9 |
0.7 |
|
19 |
2.2 |
0.9 |
|
20 |
2.3 |
0.9 |
|
Тестирование |
– |
5 |
|
Всего |
140.1 |
60.4 |
, мин
, минЗдесь: 
, 
, ‑ время, затраченное экспертом на решение комплекта задач
соответственно вручную и в среде обучающей программы.
Анализ табл. 1 говорит о том, что применение разработанной обучающей программы
для автоматизации вычислений дает заметный выигрыш в затратах учебного времени
по сравнению с расчетами вручную (почти в 2,5 раза) и дополнительно позволяет осуществить тестирование с проставлением
оценки для осуществления входного контроля знаний и умений.
Отметим, что за вычетом времени, отводимым
на вводную часть (15 мин) и заключительную часть (5 мин) занятия, на решение
задач остается 70 мин учебного времени. За это время при проведении занятия в
традиционной форме (без применения компьютеров) удается, как правило, решить
7-8 задач.
На решение всего комплекта из 20 задач с
использованием обучающей программы экспертом затрачено 55,4 мин. Таким образом,
можно предположить, что, используя возможности обучающей программы, за 70 мин
учебного времени число задач, решаемых на данном практическом занятии можно существенно
увеличить (ориентировочно с 7-8 до 20 штук).
Проверка
этого предположения (гипотезы) и является содержанием второго проверочного этапа
педагогического эксперимента. На этом этапе в двух примерно равноценных по
успеваемости учебных группах, контрольной и экспериментальной, было проведено
обсуждаемое практическое занятие соответственно по традиционной методике и с применением
обучающей программы. Курсантам предлагались задачи описанного выше комплекта. В
контрольной группе (традиционная методика) 2 курсанта решили 4 задачи комплекта
заданий, 3 курсанта решили 5 задач, 4 курсанта решили 6 задач и лишь 2 курсанта
из 11 решили 2 задачи. В экспериментальной группе два курсанта решили 18
заданий. Четыре человека из 11 решили 19 заданий. Кроме того, хорошо успевающие
курсанты (5 человек) смогли решить все двадцать задач.
Третий
итоговый этап педагогического
эксперимента был реализован в форме проверки остаточных знаний курсантов
контрольной и экспериментальной групп в
конце семестра. Курсантам была предложена 45-минутная самостоятельная
работа, в которой требовалось решить вручную 4 задачи. Результаты оценивания
приведены в табл. 2.
Для количественной оценки эффективности
обсуждаемой методики рассмотрим принятые в педагогических исследованиях
коэффициент успешности 
и коэффициент качества
подготовки курсантов
[3]:
, 
,
где m – число положительных оценок, k– число
хороших и отличных оценок, n – общее
число оценок в группе.
Таблица 2 - Результаты контроля остаточных знаний
|
Оценка Количество курсантов в группах |
2 |
3 |
4 |
5 |
Средний балл |
|
Контрольная группа (11 человек) |
2 (%) |
3 (%) |
4 (%) |
2 (%) |
3.54 |
|
Экспериментальная группа (11 человек) |
– (0%) |
2 (0%) |
4 (%) |
5 (%) |
4,27 |
В соответствии с табл.
2 получим: для контрольной группы 
, 
; для экспериментальной группы 
, 
.
Как видим, коэффициент успешности в
экспериментальной группе по сравнению с контрольной выше на 18%, а коэффициент
качества выше на 28%. Это позволяет сделать вывод, что предлагаемая методика
проведения практического занятия «Матричные и числовые характеристики неориентированных
графов» с использованием обучающей программы [2]
эффективна по критериям общей успешности и качественному показателю.
Таким
образом, гипотеза о том, что автоматизация рутинных вычислений средствами обучающей программы [2] приведет к повышению качества обучения курсантов нахождению
матричных и числовых характеристик неориентированных графов, подтверждена педагогическим
экспериментом.
Литература:
1. Паршин А.В. Математические модели и
специальные программно-технические средства обучения курсантов математике в
военных вузах: монография. Воронеж: ВАИУ, 2009. 270 с.
2. Паршин А.В., Панюшкин В.Н., Малимон
М.С. Автоматизированное практическое занятие «Матричные и числовые
характеристики неориентированных графов» // Свидетельство о государственной
регистрации программы для ЭВМ №2013613817, зарегистрирована 16 апреля 2013 г.
М.: Роспатент, 2013. 66 с.
3. Якунин В.А. Психология учебной
деятельности студентов. М.-Спб.: Логос, 1994. 160 с.