Тезисы доклада Математическая физика
К.ф-м.н. Скворцов Г.Е.
Санкт-Петербургский государственный
университет
К.ф-м.н. Перевозников Е.Н.
Санкт-Петербургский государственный
торгово-экономический университет
Динамические качественные переходы
Рассматривается метод получения критериев динамических переходов основанных на
использовании сингулярностей в
динамических моделях физических систем. Приведен пример демонстрирующий метод.
1. Динамический
качественный переход (ДКП) – существенное изменение структуры или динамического
режима физической системы в условиях сильной неравновесности. ДКП, в отличие от известных равновесных
фазовых или структурных переходов, обладает рядом существенных особенностей:
а) условия возникновения и
описания значительно отличаются от равновесных;
б) происходят при
существенной неравновесности системы;
в) сопровождаются
неустойчивым переходным состоянием,
которому соответствует математическая особенность.
Существование математических особенностей в динамических
моделях можно использовать как условие существования ДКП.
Связь физических и математических особенностей известна давно и используется для
классификации фазовых переходов (скачек физических величин или их производных).
Однако процесс перехода не имеет общего описания и общего критерия, хотя
изучение различных феноменов сопровождающих эти переходы, например режимы обострения, динамического
хаоса и т.д., вызывают повышенный интерес /1,2,3/.
В настоящей работе предлагается способ использования
сингулярностей динамических моделей для определения условий существования ДКП и
их описания.
2. Характерными
математическими сингулярностями
являются точки ветвления (бифуркации), уголки, скачки, острый резонанс,
стремление величин или их производных к бесконечности. Представляет интерес и
время возникновения и реализации сингулярности.
В динамических моделях описываемых системой дифференциальных
уравнений для определяемых величин
![]() ,(1)
,(1)
сингулярности проявляются в
зависимости функции - ![]() от
от ![]() , времени-
, времени- ![]() , параметров-
, параметров-![]() . Алгоритм предлагаемого сингулярно – динамического метода
. Алгоритм предлагаемого сингулярно – динамического метода
(СД) состоит: а) выявление по виду функции ![]() сингулярностей;
сингулярностей;
б) упрощение динамических уравнений с использованием сингулярностей;
в) качественный анализ
уравнений;
г) решение упрощенных
уравнений и определение времени развития ДКП.
Совокупность полученных
согласованных результатов приводит к формулировке критерия ДКП.
3. Продемонстрируем метод на примере простой решаемой модели,
заданной уравнением вида
![]() (2)
(2)
![]() - положительные
параметры динамической одномерной системы, r-
ресурс вводимый или выводимый из системы.
- положительные
параметры динамической одномерной системы, r-
ресурс вводимый или выводимый из системы.
Указываем ![]() набор сингулярностей:
набор сингулярностей:
![]() ;(3)
;(3)
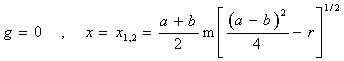 ;(4)
;(4)
![]() ;(5)
;(5)
![]() .(6)
.(6)
Особенности (6) обусловлены
значениями r. Величины ![]() становятся
комплексными при
становятся
комплексными при
![]() .
(7)
.
(7)
Эти особенности необходимо учитывать, поскольку они являются
границами изменения режимов.
Выясняем какие из указанных
сингулярностей приводят к ДКП. Прежде всего качественным переходом является
стремление определяющей величины к бесконечности, как показывает локальный
анализ это возникает при ![]() , время развития ДКП при этом определяется соотношением
являющееся его критерием
, время развития ДКП при этом определяется соотношением
являющееся его критерием
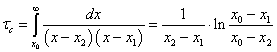 .(8)
.(8)
Особый режим возникает при
условии (7), когда
![]() .
.
С ростом r значения ![]() переходят в комплексную плоскость и критерий
переходят в комплексную плоскость и критерий
ДКП приобретает вид
![]() ,(9)
,(9)
c и d выражаются через исходные параметры согласно
(4).
Наряду с демонстрацией СД метода обнаруживающий рад ДКП в простой
модели, динамическая система испытывает существенный ДКП вплоть до разрушения как при вводе ресурса
сверх граничного, так и при выводе его.
4. Представленный
сингулярно-динамический метод по сути
является динамической теорией катастроф и обладает рядом преимуществ по сравнению с используемыми методами
обнаружения качественных переходов и
связанных с ними неустойчивостями. Теория Ляпунова не описывает качественные
переходы, а лишь указывает на
возрастающее отклонение от исходного режима и в предельном, нейтральном варианте может использоваться
для обнаружения динамических бифуркаций. В этом виде он доведен до удобного НРИ метода / 3 /, с
помощью которого обнаружен целый ряд ДКП. Предложенный СД – метод не только
указывает начало ДКП, но и определяет условия и время его реализации.
Литература
1.
1. М..Кузнецов С.П.
Динамический хаос, ФМ. М. Физматгиз,2006.355 с.
2.
2. Перевозников Е. Н.,
Скворцов Г. Е., К теории устойчивости
неравновесных систем, ЖТФ, 52, вып. 12,1982, с (2353 - 2359).
3.
3. Перевозников
Е.Н. , Скворцов Г.Е., Динамика
возмущений и анализ устойчивости неравновесных систем , СПТЭИ, 2010, (137)с.
4.
4. Перевозников
Е.Н.,Критерий устойчивости нелинейных систем, Изв.Вузов, физика ,№ ., 2013,( ).