Korniyenko B.Y.

National aviation university, Ukraine

Characteristics of the production of mineral fertilizers in a fluidized bed granulator

Community development in modern conditions depends on the development and implementation of energy efficient environmentally friendly technologies. Application of technique of fluidization for obtaining solid composites with desired properties in the presence of phase transitions allows to combine a number of technological stages by the thermal coefficient of more than 60%. The creation of mathematical models for the purpose of creation modern systems of management processes in disperse systems is relevant [1].

Granulation processes are different both in the methods of implementation, and in the hardware design. One of the promising methods is an obtaining of a granular product in a fluidized bed apparatus.

The aim of the article is to study the static and dynamic characteristics of the mathematical model of a fluidized bed granulator during the intensive heat and mass transfer processes in the manufacture mineral fertilizers.

Feature of the process of formation of solid humic-mineral composites is uniform distribution of mineral and humic substances throughout the volume of grain and in physical and mechanical properties: spherical shape, diameter 1.5 - 4.5 mm, strength ≥ 10 N/grain. This solution dispersed in two-phase system: granular material - gas coolant.

Liquid phase by the action of adhesive and sorption forces sticks to the surface of solid particles in a superfine film. The porous structure of granules causes partial diffusion of moisture. To films from hot solid particles and gas coolant supplied heat. This leads to intense evaporation of the solvent resulting in the surface of solid particles formed a thin layer of microcrystals mineral substance and deposited between colloidal particles of humic compounds. Further microcrystals serve as centers of crystallization of minerals with another liquid film, resulting in increasing the size of granules.

There are several approaches to the mathematical modeling of dehydration and granulation in fluidized bed.

Granular material is fluidized chaotic system. For the mathematical modeling of fluidized bed apparatus is also chaotic hydrodynamics.

Very effective are attempts to explore the hydrodynamics of multiphase processes in a fluidized bed apparatus using mikrobalance models. These mathematical models solved to bind the equation of conservation of energy considering the interfacial interaction. For multivariate modeling processes of dehydration and granulation in fluidized bed using two-phase Euler-Euler model.

Transport equation of temperature granules taken into account convective heat transfer, solid phase voltage, flow fluctuation energy scattering energy collisions, the energy exchange between the phases. It is possible to determine the intensity of the interaction of the gas (solid) environment and solid particles (dispersed phase) at different hydrodynamic regimes and the corresponding temperature change granules during dehydration and granulation [2].

Mathematical model [2] fully takes into account the process, but a large amount of calculation time complicates its use in driving the process of dehydration and granulation in fluidized bed in real conditions.

Therefore, use slightly simplified mathematical model of its structure corresponds to the model described above, but significantly improves its adaptation in driving the process of dehydration and granulation in a fluidized bed.

According to the results of experimental researches it was found that for the kinetics of the process of obtaining a stable final product with desired physical and chemical properties in fluidized bed granulation prerequisite is respect given temperature in the layer. Therefore, to research the static and dynamic characteristics of selected mathematical model with lumped parameters - the ultimate coolant temperature and temperature fluidized bed.

The dynamics of thermal balance coolant-air can be described by the following equation:

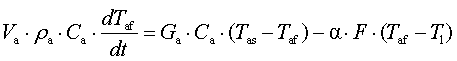; (1)

where T_as, T_af– initial and final air temperature, К; T_l – temperature layer, К; F– surface mass transfer, м²; α– heat transfer coefficient, W/м²·К; G_a– air flow, м³/с ; C_a– heat capacity of air, J/kg·К; V_a– the air volume, м³; ρ_a– air density, kg/м³.

Dynamics of heat balance particle fluidized bed is described as follows:

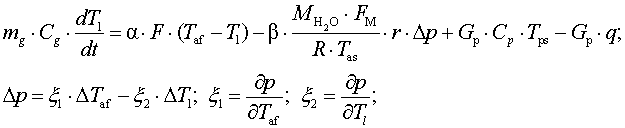(2)

_{where β – coefficient of mass recoil, м/s; МH2O – molecular weight of water, kg/mol; F – mass of transfer surface, м2; FM – particle surface, м2; R – universal gas constant, J/(mol·К); mg– mass of granule, kg; Сg - specific heat of the material granule, J/kg·К; Gр – expenditures of solution, kg/с; Δр – difference of partial pressures, Pа; xp – moisture content of the material; Трs – initial temperature of the solution, К;Ср - heat capacity of solution, J/kg·К; r– heat of vaporization, J / kg; q - heat released by crystallization solution, J/kg.}

_{Possible channels "expenditures coolant-temperature fluidized bed", "cost solution - temperature fluidized bed."}

For static characteristics are equation based finite temperature and the temperature of the layer changes the air flow and solution:

; (3)

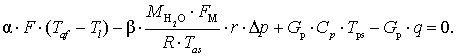(4)

From equations (3) - (4) we obtained an expression for the temperature fluidized bed:

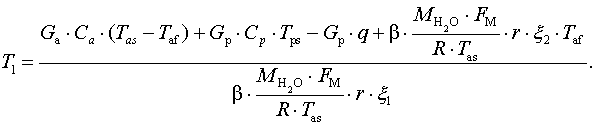(5)

Conclusion

This mathematical model describes the static and dynamic characteristics of the process in a fluidized bed granulation and shows the change in coolant temperature and fluidized bed during the heat-mass transfer processes in moving granular material through appropriate technological zone in the apparatus, which providing granular product with the desired properties.

The variation of temperature determines the granulation kinetics and physical and mechanical properties of the pellets. Therefore, the proposed mathematical model can be used to create an effective system of control the process of formation of mineral fertilizers in the fluidized bed with liquid dehydration systems.

Bibliography

1. Korniyenko B.Y. Features modeling of transport processes in disperse systems / B.Y. Korniyenko // Journal of the National Technical University of Ukraine "Kyiv Polytechnic Institute" series "Chemical engineering, ecology and resource conservation". – 2011, № 2(8). - P. 5-9.

2. Korniyenko B.Y. The dynamics of the processes of dehydration and granulation in fluidized bed / B.Y. Korniyenko // Journal of the National Technical University of Ukraine "Kyiv Polytechnic Institute" series "Chemical engineering, ecology and resource conservation". – 2012, № 1(9). - P. 15-19.