Technical sciences/1. Metallurgy

Dr.Tech.Sci.

A.V. Satonin

, Ph. D. M.G. Korenko, A.S. Churukanov,
A.A. Satonin

Donbass State Engineering Academy, Ukraine

Kryvyi Rih Metallurgical Institute of the State Higher Education Institution "National University of Kryvyi Rih", Ukraine

PJSC "Novokramatorskyi Machine-Building Plant", Ukraine

Development of numerical one-dimensional mathematical models of stress-strain state of metal at relatively cold rolling of narrow strips and sheets

One of the technological features of the cold rolling production process of relatively narrow strips and sheets is the increased degree of influence of the edge effect, which determines the levels of broadening and power parameters of the process [1]. Thus the specificity of the mechanism of formation of the boundary conditions causes a substantial modification of the scheme of stress-strain state of metal exactly on the edges of the rolled strips and sheets, which makes it necessary to account for this effect both in terms of power parameters and in terms of quantifying the degree of ductility capacity [2; 3].

Partition of the entire length of the plastic forming section to the n number of the i elementary volumes (Fig. 1) to determine the current values of normal contact stresses for each of them will produce further partitioning of the cross-section to the half of the width of the rolled strip or sheet to the final t set of j elementary volumes, performed by analogy with the methods indicated in [4].

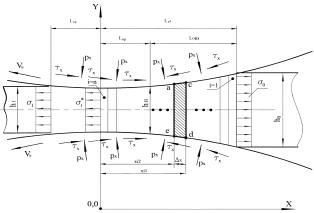
a) b)

Fig. 1. Analytical models of integral deformation zone (a) and the selected i elementary volume of plastic forming section (b) in relation to one-dimensional numerical mathematical modeling of stress-strain state of metal for cold rolling of relatively thin strips and sheets

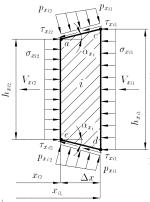
Consider the condition of static equilibrium for each of them within the design of all forces on the z-axis (Fig. 2) :

, (1)

where , are normal axial stresses acting in the initial (the final numerical index 1) and in the final (the last numerical index 2) sections, the positive values of which correspond to compressive stresses; , , , are the current values of tangential contact stresses applied to the rolled billet considering its cross section by the lower (the first numerical index 1) and upper (the first numerical index 2) roll dies; is the thickness of the rolled billet in the final boundary section of i elementary volume obtained by dividing the deformation zone along the x-axis

, (2)

; (3)

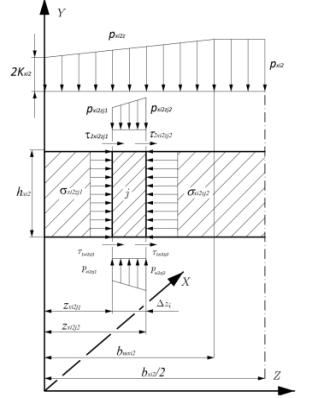
Fig. 2. Analytical model of deformation zone for numerical mathematical modeling of stress-strain state of metal on the edges for cold rolling of relatively thin strips and sheets

_{, (4)}

where is the step of partitioning width of rolled billet for j elementary volumes defined by their total number .

Based on the analytical description of the tangential contact stresses , provided that , at when plasticity condition is or equation (1) can be transformed as follows:

(5)

wherefrom, in relation to the desired values of normal contact and normal axial stresses , in its final form represent:

; (6)

, (7)

where the quantitative assessment of stresses and is known, according to the applied recurrent solution pattern, based on the results of the previous calculation of elementary cross-section ; is the current doubled value of the shear resistance along the length of the deformation zone; are the current values of the coefficients of external friction, which, according to Amontons-Coulomb law [5], characterize the value of tangential contact stresses in the deformation zone.

As a direction of the recurrent solution we used the direction from the edges of the rolled tape to its middle, i.e. the direction corresponding to the z-axis, which originates on the edge and which is perpendicular to the rolling axis (see Fig. 2). With this in mind, the initial conditions and the connection conditions of the applied recurrent pattern comply with:

(8)

. (9)

Direct numerical recurrence solution, taking into account the symmetry of cross-sections of the deformation zone, is produced only for one of the edges (see Fig. 2), completing it as equality of normal contact stresses, obtained by calculating the length and breadth of the rolling axis, i.e. as a fulfillment of the condition .

Thus, the geometric coordinate , corresponding to the beginning of the present condition, is taken for the length of the zone of high broadening for each of the edges.

With a regard to the quantitative assessment of the sequence number of j elementary section , the average integral value of normal contact stresses for i cross-section of the entire deformation zone is also determined:

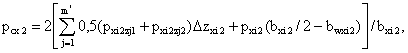(10)

It is the knowledge, which is necessary for the subsequent numerical integration by the i recurrent solution procedure and determination of integral value of rolling force in the zone of plastic forming of metal taking into account the presence of the edge effect:

(11)

In general, the presented dependences (6)–(11) contributed to the mathematical software subprogram specifying numerical mathematical models of the processes of symmetric and asymmetric rolling of relatively narrow strips and sheets. As an example of the results of numerical realization of the obtained software figure 3 shows calculated normal distribution of contact stresses within the cross-section width of the deformation zone.

Analysis of the obtained results have proved that the edge effect, taken into account, leads to the decrease of average integral value of normal contact stresses , and, consequently, to the reduction of the integral value of the rolling force. The degree of refinement on the calculation of the rolling force is in the range 5...15 %, the larger values of which correspond to the rolling of more narrow strips and sheets.

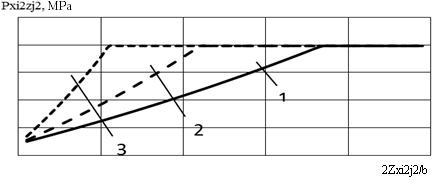
b = 30 мм; 2 – b = 50 мм; 3 – b = 100 мм

Fig. 3. Estimated normal distribution of contact stresses within the width of the zone of deformation at cold rolling of brass CW508L; (DIN: 2.0321) by reversing mill 250

The obtained theoretical solutions (6), (7) are used as the initial data for calculation of the employment degree of rolled metal plasticity capacity, implemented on the basis of V.A. Ogorodnikov’s methodology [3; 4], and, consequently, with the regard to the improvement of technological modes of intermediate annealing and subsequent cold rolling of relatively thin strips and sheets.

On the basis of the numerical approach, which intends splitting the deformation zone along its length and width, followed by recurrent solution of the conditions of static equilibrium of allocated elementary volumes, numerical mathematical models of rolling processes of relatively thin and narrow tapes and sheets have been specified, which provide for the accounting of the edge effect. Thus the degree of qualifying the rolling force, as demonstrated by the quantitative evaluation of the obtained results, is in the range 5...15 %, and the degree of qualifying the employment of plasticity capacity of rolled metals or alloys corresponds to 10...20 %.

References:

1. Сатонин А. В. Расчет напряжений и деформаций по кромкам прокатываемых лент и полос / А. В. Сатонин, М. Г. Коренко, И. С. Сухоруков // Восточно-европейский журнал передовых технологий. – 2011. – Вып. 5/7. – С. 63–66.

2. Колмогоров В. Л. Напряжение. Деформация. Разрушение / В. Л. Колмогоров. – М. : Металлургия, 1970. – 229 с.

3. Огородников В. А. Оценка деформируемости металла при обработке давлением / В. А. Огородников. – К. :Вищашк., 1983. – 175 с.

4. Федоринов В. А. Математическое моделирование напряжений, деформаций и основных показателей качества при прокатке относительно широких листов и полос : монография / В. А. Федоринов, А. В. Сатонин, Э. П. Грибков. – Краматорск : ДГМА, 2010. – 156 с.

5. Целиков А. И. Теория продольной прокатки / А. И. Целиков, Г. С. Никитин, С. Е. Рокотян. – М. : Металлургия, 1980. – 320 с.