Боловин Е.В
Студент, Кафедра Электропривода и Электрооборудования,
Национальный Исследовательский Томский Политехнический Университет, Томск,
Россия
Динамическая идентификация
параметров асинхронного двигателя на основе разностных схем с использованием
датчиков напряжения, тока и скорости
Реферат
В данной
статье будет представлена методика идентификации параметров асинхронного
двигателя с использованием информации, получаемой с датчиков тока, напряжения и
скорости.
Ключевые слова: асинхронный двигатель, разностные
схемы, идентификация
Введение
Асинхронные
двигатели благодаря своим известным преимуществам, таким как, простая
конструкция, надежность, прочность и низкая стоимость, нашли очень широкое
промышленное применение. Для повышения производительности, улучшения
статической и динамической работы электродвигателя используют преобразователи
частоты, которые используют скалярное и векторное управление. Оба метода
управления во многом зависят от правильной оценки параметров асинхронного
двигателя и очень чувствительны к их изменению. Таким образом, необходимо
постоянно следить за изменением значений параметров двигателя и определять
значения оценок параметров с минимальной погрешностью и в кратчайшие сроки.
Идентификация параметров асинхронного двигателя
Рассмотрим
метод идентификации параметров динамического объекта, описанного системой
дифференциальных уравнений четвертого порядка, а именно асинхронного двигателя
с короткозамкнутым ротором на основе разностных схем с использованием датчиков
угловой скорости вращения вала, токов и напряжений статора.
Математическую
модель асинхронного двигателя при общеизвестных допущениях [1] можно составить
записать следующим образом:
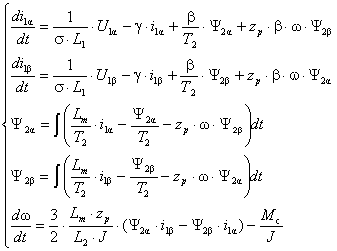 (1)
(1)
где ![]()
![]()
![]() T2 – постоянная времени.
T2 – постоянная времени.
R1 – активное
сопротивление обмотки статора, Ом;
R'2 – приведенное к статору активное
сопротивление ротора, Ом;
L1=L1σ+Lm – эквивалентная индуктивность обмотки статора,
Гн;
L2=L′2σ
+Lm – эквивалентная индуктивность обмотки ротора,
Гн;
L1σ – индуктивность рассеяния обмотки статора, Гн;
L'2σ – приведенная к статору индуктивность
рассеяния обмотки ротора, Гн;
Lm – результирующая индуктивность, обусловленная
магнитным потоком в воздушном зазоре машины, Гн;
 – эквивалентное
сопротивление двигателя, Ом;
– эквивалентное
сопротивление двигателя, Ом;
![]() –
синусоидальная по форме составляющая напряжения статора по оси α
ортогональной неподвижной системы координат α, β, В;
–
синусоидальная по форме составляющая напряжения статора по оси α
ортогональной неподвижной системы координат α, β, В;
![]() – косинусоидальная по форме составляющая
напряжения статора по оси β ортогональной неподвижной системы координат
α, β, В;
– косинусоидальная по форме составляющая
напряжения статора по оси β ортогональной неподвижной системы координат
α, β, В;
![]() –
амплитудное значение фазного напряжения статорной обмотки, В;
–
амплитудное значение фазного напряжения статорной обмотки, В;
U1– действующее значение фазного напряжения
статорной обмотки, В;
f1 – частота напряжения статора, Гц;
i1α, i1β – составляющие тока
статора (фазные токи обмотки статора) в системе координат α, β, А;
Ψ2α,
Ψ2β – составляющие потокосцепления ротора в системе
координат α, β, Вб;
Мэм – электромагнитный момент двигателя, Н·м;
Мс – момент статического сопротивления на валу
двигателя, включая собственный момент трения двигателя, Н·м;
![]() –
коэффициент рассеяния;
–
коэффициент рассеяния;
J – момент инерции двигателя, кг·м2.
После
многочисленных постановок и замен в системе (1) получаем уравнение (2):
 (2)
(2)
где![]()
![]()
![]()
![]()
![]()
С учётом
интервала Δt дискретизации по
времени измерительной системы перейдём от дифференциального уравнения (ДУ) к
системе разностных уравнений (РУ), записанных в матричном виде относительно
текущего tj и предыдущих tj-x·k=tj-Δt·k моментов времени при условии постоянства
оценок параметров, где x=0, 1, 2,…5; k – коэффициент временной задержки.
![]() (3)
(3)
где 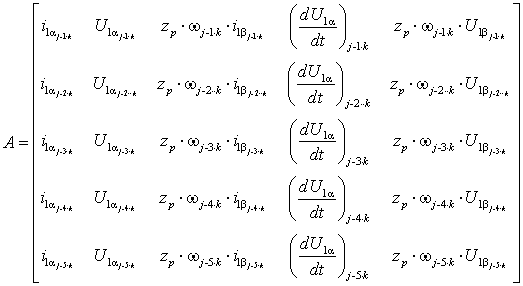
это матрица связи между
неизвестными параметрами и внешними воздействиями, а

– матрица внешних
воздействий, K=[K1, K2,
K3, K4, K5]Т-вектор
неизвестных параметров. В выше
приведенных матрицах ![]() – составляющие тока статора (фазные токи обмотки
статора) в системе координат α, β;
– составляющие тока статора (фазные токи обмотки
статора) в системе координат α, β;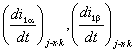 – первые производные токов статора (фазные токи обмотки
статора) в системе координат α, β;
– первые производные токов статора (фазные токи обмотки
статора) в системе координат α, β; 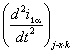 – вторые производные токов по оси α;
– вторые производные токов по оси α; ![]() – составляющие напряжения статора по оси α и
β;
– составляющие напряжения статора по оси α и
β; ![]() – производные напряжения статора по оси α на j, j-1·k, j-2·k,…, j-5·k шагах соответственно.
– производные напряжения статора по оси α на j, j-1·k, j-2·k,…, j-5·k шагах соответственно.
Для
нахождения оценок параметров системы, вычислим коэффициенты ![]() решив систему
уравнений (3) методом наименьших квадратов:
решив систему
уравнений (3) методом наименьших квадратов: ![]()
После
нахождения коэффициентов, определим оценки параметров АД следующим образом:
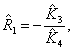
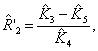
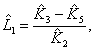
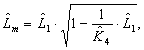

![]()
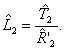
Заключение
Представлена
процедура составления разностных уравнений для идентификации параметров асинхронного
двигателя, позволяющий определять оценки приведенного
к статору активного сопротивления ротора, эквивалентной индуктивности обмотки
ротора, эквивалентной индуктивности обмотки статора, результирующей
индуктивности, обусловленной магнитным потоком в воздушном зазоре машины,
эквивалентной постоянной времени цепи ротора асинхронного двигателя короткозамкнутым ротором. Данная процедура может применена
в адаптивных системах управления электроприводами.
Список
использованной литературы:
1. Cincirone, M., M. Pucci, G. Cincirone, and G. A. Capolino. A new
experimental application of least-squares techniques for the estimation of the
parameter of the induction motor // IEEE Trans. on Ind. Applications. Sep.
2003. Vol. 39, No. 5. С. 1247–1255.