Каряченко Н.В.
Національна металургійна
академія України
ДОСЛІДЖЕННЯ ПОПЕРЕЧНИХ КОЛИВАНЬ
ОДНОМІРНИХ
ГНУЧКИХ РОБОЧИХ ОРГАНІВ вантажотранспортуючих ПРИСТРОЇВ З
РУХОМИМ інерційнИМ навантаженняМ
У цій статті розглядається задача про
поперечні коливання одномірних гнучких робочих органів вантажотранспортуючих
пристроїв, призначених для транспортування штучних вантажів, дискретно
закріплених на гнучкому тяговому органі, виконаному у вигляді одного або
декількох паралельних канатів, ланцюгів, стрічок. Вона зводиться до розв'язання
лінійних диференціальних рівнянь гіперболічного типу зі змішаною похідною [1].
Застосування класичної схеми розподілу змінних в дійсній області шуканих
функцій часто призводить не тільки до кількісних, а й до якісних погрішностей.
Розподіл змінних некласичним способом, в основу якого покладено вибір рішення у
вигляді спеціального двочленного уявлення, дозволяє більш точно описати
динамічні процеси, що відбуваються в таких системах, без яких неможливо
правильне проектування і безпечна експлуатація підйомних і транспортних
установок.
Вивченню динаміки механічних
об'єктів, таких як, канат, струна, балка, комбіновані системи, окремі випадки
пластинок і оболонок, що знаходяться під впливом рухомого інерційного
навантаження, присвячені численні дослідження. У роботах, в яких рішення
рівнянь руху будується за допомогою методу двохвильового уявлення, в основному,
розглядаються системи з рівномірно розподіленим по довжині масовим
навантаженням. Водночас, наявність у ньому зосереджених вантажів істотно
впливає на якісну картину і кількісні характеристики динамічних процесів
досліджуваних об'єктів.
Побудуємо рішення диференціального
рівняння поперечних коливань одномірного гнучкого робочого органу
вантажотранспортуючого пристрою з рухомим розподіленим і зосередженим
інерційним навантаженням в загальному вигляді. Після переходу до безрозмірних
координат, часу і введення малого параметра ![]() [2], однорідне диференціальне рівняння, що
описує поперечні коливання, і граничні умови, що описують відсутність
поперечних переміщень в крайніх точках розглянутої ділянки каната між опорами,
мають вигляд:
[2], однорідне диференціальне рівняння, що
описує поперечні коливання, і граничні умови, що описують відсутність
поперечних переміщень в крайніх точках розглянутої ділянки каната між опорами,
мають вигляд:
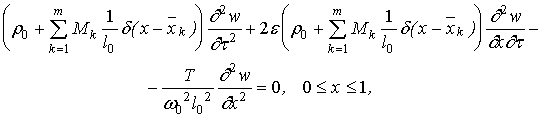 (1)
(1)
![]() (2)
(2)
де x - безрозмірна координата ; r0 - маса одиниці довжини
гнучкого робочого органу (канату); Mk - маса k-го
зосередженого вантажу; l0 - довжина прольоту;
![]() - безрозмірна координата k-го вантажу, що визначає його положення в будь-який момент часу; xk - безрозмірна координата, що
визначає положення k-го вантажу в
початковий момент часу; t - безрозмірний час;
- безрозмірна координата k-го вантажу, що визначає його положення в будь-який момент часу; xk - безрозмірна координата, що
визначає положення k-го вантажу в
початковий момент часу; t - безрозмірний час; ![]() - дельта - функція Дірака; w(x,t) - поперечне відхилення; Т - натяг каната; w0 - власна перша частота
коливань однорідного каната довжиною l0,
закріпленого по кінцях; v - швидкість руху.
- дельта - функція Дірака; w(x,t) - поперечне відхилення; Т - натяг каната; w0 - власна перша частота
коливань однорідного каната довжиною l0,
закріпленого по кінцях; v - швидкість руху.
Запишемо рівняння ( 1 ) в більш
зручному для вирішення вигляді:
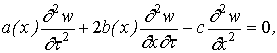 (3)
(3)
де
 (4)
(4)
Розв'язання лінійного
диференціального рівняння другого порядку гіперболічного типу зі змішаною
похідною (1) візьмемо у вигляді спеціального двочленного уявлення [3]
![]() (5)
(5)
де j (x) і y(x) - функції, що задовольняють граничним умовам.
Продиференцюємо вираз (5)
необхідну кількість разів по змінним x і t та підставимо в (3)
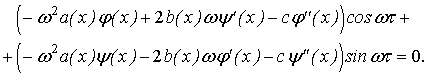
Враховуючи, що ![]() і
і ![]() - лінійно незалежні функції, прирівнюємо нулю в
останній залежності множники при них
- лінійно незалежні функції, прирівнюємо нулю в
останній залежності множники при них
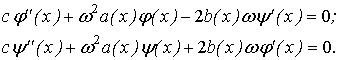
В отриманій для визначення функцій
![]() і
і ![]() системі диференціальних рівнянь друге рівняння
помножимо на
системі диференціальних рівнянь друге рівняння
помножимо на ![]() і складемо з першим
рівнянням [4]
і складемо з першим
рівнянням [4]
![]()
Отримане таким чином рівняння
представимо так:
![]() (6)
(6)
де
![]() (7)
(7)
Функції ![]() і
і ![]() відповідно до (7) визначаються за такими формулами
відповідно до (7) визначаються за такими формулами
![]() (8)
(8)
На основі граничних умов (2)
функції ![]() і
і ![]() задовольняють нульовим крайовим умовам
задовольняють нульовим крайовим умовам
![]()
тому і функція ![]() теж підпорядкована нульовим граничним умовам
теж підпорядкована нульовим граничним умовам
![]() (9)
(9)
Підставимо в рівняння (6) вирази
коефіцієнтів (4)
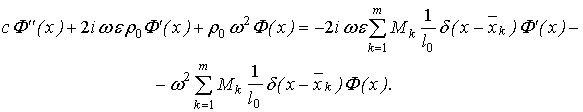
Використовуючи перетворення Лапласа перейдемо в
останньому записі до зображення функції ![]() , враховуючи
першу граничну умову (9). Зображення
, враховуючи
першу граничну умову (9). Зображення ![]() отримаємо у вигляді:
отримаємо у вигляді:
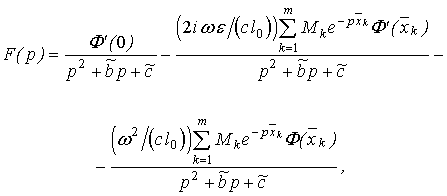 (10)
(10)
де ![]()
Переходячи в (10) назад до оригіналу,
врахуємо, що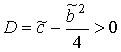
і позначивши ![]() , отримаємо вираз для форм коливань,
, отримаємо вираз для форм коливань, 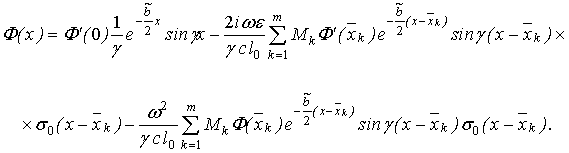 (11)
(11)
Побудувавши
рекурентні співвідношення ![]() та
та ![]() , після необхідних обчислень
, після необхідних обчислень ![]() запишеться
запишеться
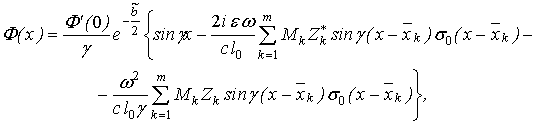 (12)
(12)
де функції ![]() і
і ![]() знаходяться з
побудованих рекурентних залежностей, записаних у компактній і зручній для
застосування ЕОМ формі
знаходяться з
побудованих рекурентних залежностей, записаних у компактній і зручній для
застосування ЕОМ формі
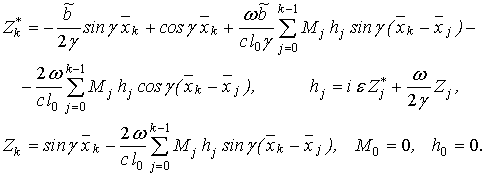 (13)
(13)
Тут 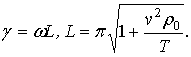
На підставі другої граничної умови ![]() , одержимо характеристичне рівняння для визначення частот
коливань
, одержимо характеристичне рівняння для визначення частот
коливань
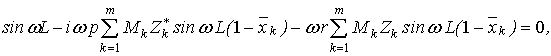 (14)
(14)
де 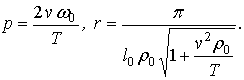
Визначивши корені рівняння (14) wn одним з чисельних методів, після підстановки
їх у (12), вираз для форм коливань буде
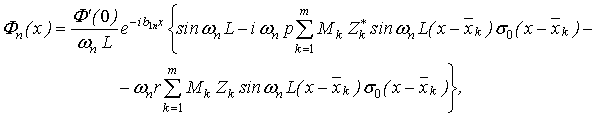
де ![]()
Враховуючи (7), повний розв'язок
диференціального рівняння поперечних коливань канатів (1), що складається з
суми частинних рішень, одержимо у вигляді
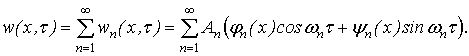
Отриманий розв'язок дозволяє визначати частоти,
форми власних і "супроводжуючих" коливань системи, характер їх зміни
в залежності від швидкості при будь-якій кількості зосереджених вантажів,
значень їх мас і розташування між опорами.
Література.
1.
Горошко О.А., Савин Г.Н. Введение в механику одномерных деформируемых тел
переменной длины. К.: Наук. думка, 1971.
2.
Каряченко Н.В. Дифференциальное уравнение поперечных колебаний канатов
грузотранспортирующих устройств с подвижной инерционной нагрузкой в общем виде
// Материалы IX научно-практической конференции «Дни науки-2013». Прага. –2013.
– Т.34. – С. 21-24.
3.
Горошко О.О., Дем’яненко А.Г., Кіба С.П. Двохвильові процеси в механічних системах. К.:
Либідь, 1991.
4. Колесник
И.А., Каряченко Н.В. Колебания механических звеньев устройств, несущих подвижную
инерционную нагрузку // Польско-Украинский семинар “Теоретические основы
строительства”. Дн-ск.: ПГАСУ. Ч. 2. С. 237-241.