Химия и
химические технологии/8. Кинетика и катализ
К.х.н.,
доцент Телеш А.Д.
Таганрогский
политехнический институт – филиал ДГТУ, Россия
Кинетика
взаимодействия боксита с серной кислотой
Для высококремнистого алюминийсодержащего сырья более рациональными, перед традиционными щелочными способами, становятся кислотные методы переработки, в частности сернокислотный [1], позволяющие уже в самом начале технологического процесса провести селективное отделение кремнезёма, сократив материальные потоки.
Нами изучалась кинетика процесса сернокислотного выщелачивания лигнитового боксита следующего состава, %: Al2O3 – 42,31; Fe2O3 – 5,58; FeO – 1,93; SiO2 – 22,52; CaO – 1,96; MgO – 0,60; TiO2 – 0,40; CO2 – 1,10; потери при прокаливании – 25,50.
Эксперименты проводили в реакторах из термо- и химическистойкого стекла, снабжённых рубашками, соединенных с термостатом, обратными холодильниками и электрическими мешалками.
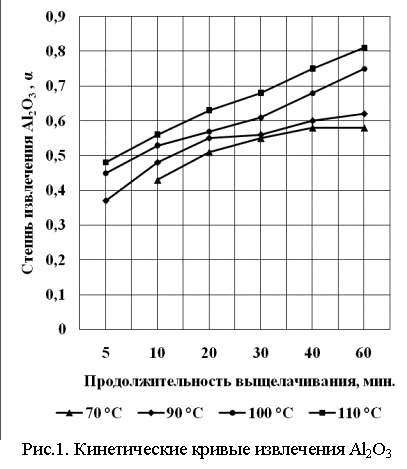
Измельчённый до крупности ~0,2 мм боксит помещали в реакторы, куда добавляли необходимое количество предварительно подогретой до температуры опыта серной кислоты 60 % концентрации и включали перемешивание, скорость которого была постоянной и равной 60 об./мин. Массовое отношение Ж:Т = 2 в каждом опыте. Кинетические кривые, отражающие зависимость степени извлечения алюминия от времени и температуры, показаны на рис.1.
Математическая обработка
полученных результатов заключалась в подборе теоретических кинетических
уравнений для описания экспериментальных данных. Были применены уравнения
Яндера и Гинстлинга-Броунштейна [2], Журавлёва-Лесохина-Темпельмана [3],
Ерофеева-Колмогорова, Рогинского, Саковича [4, 5], а также эмпирическое
уравнение, предложенное для описания кинетики сернокислотного разложения
глинистой руды [6]. Уравнения приводились к виду, где зависимость степени
превращения α от времени τ носила линейный характер. Затем
проводилась аппроксимация полученной зависимости полиномом первого порядка.
Требовалось найти такое уравнение с оценкой его параметров, чтобы дисперсия
адекватности расчётной прямой была минимальной.
Экспериментальные данные лучше всего описывается уравнением, по форме совпадающим с уравнением Ерофеева-Колмогорова, которое можно представить в виде:
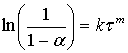 , (1)
, (1)
где α – степень извлечения; k – константа скорости; τ – продолжительность выщелачивания; m – параметр, зависящий от механизма реакции, геометрии частиц, гидродинамических условий образования центров кристаллизации и степени гидратации.
Данное уравнение описывает образование центров кристаллизации и его отличие от уравнения Ерофеева-Колмогорова заключается в физическом смысле параметра m. Возможность использования этого уравнения можно обосновать диффузией ионов гидроксония к активным центрам минералов, существование которых предполагается ещё до начала взаимодействия с кислотой. В дальнейшем при выщелачивании происходит уменьшение удельной поверхности частиц и числа активных центров. Одновременно на месте последних образуются зародыши продуктов реакции, которые параллельно гидратируются и диффундируют в раствор [7]. Уравнение образования центров кристаллизации было с успехом использовано при обработке кинетических кривых взаимодействия каолинита с серной кислотой [7].
Найденные по уравнению (1) кинетические параметры приведены в табл.1. Там же даны значения дисперсии адекватности при аппроксимации кинетических зависимостей, представленных в координатах ln[ln(1/(1-α))] – lnτ, полиномом первого порядка.
Таблица 1. Результаты обработки кинетических кривых разложения боксита серной кислотой
|
Температура, оС |
ln k |
m |
Sад. |
|
70 |
-1,13 |
0,26 |
0,053 |
|
90 |
-1,16 |
0,29 |
0,069 |
|
100 |
-1,05 |
0,32 |
0,073 |
|
110 |
-1,05 |
0,36 |
0,056 |
Энергия активации (E) и предэкспоненциальный множитель (ko) уравнения Аррениуса для реакции извлечения Al2O3 были найдены из линейной зависимости ln k от 1/T методом наименьших квадратов. Уравнение Аррениуса при этом имеет вид [8]:
![]() . (2)
. (2)
Рассчитанные значения энергии активации и натуральный логарифм предэкспоненциального множителя для процесса разложения глинозёмсодержащих минералов боксита составляют 2,53 кДж/моль и -0,26, соответственно. Низкая величина энергии активации свидетельствует о протекании процесса в диффузионной области.
Литература:
1. Маматов Э.Д., Хомиди Абдул
Куддус. Разложение алюминийсодержащих руд с применением серной кислоты и газообразного
хлора. – Международный
научный журнал, № 6, 2015.
2. Вольдман Г.М., Зеликман
А.Н. Теория гидрометаллургических процессов. – М.: Интермет Инжиниринг, 2003. –
464 с.
3. Будников П.П., Гинстлинг
А.М. Реакции в смесях твёрдых веществ. – М., 1971. – 490 с.
4. Янг Д. Кинетика разложения
твёрдых веществ. – М.: Мир, 1969. – 264с.
5. Розовский А.Я. Кинетика
топохимических реакций. – М.: Химия, 1974.– 224 с.
6. Sancho J.P., Verdeja L.F., Llavona M.A. Kinetic parameters of
aluminium extraction from Spanish clays with sulfuric acid. – Trav. Com. Int.
etude bauxite, alumina et alum., 1983, v. 13, № 18, p. 315-321.
7. Лайнер Ю.А. Комплексная
переработка алюминийсодержащего сырья кислотными способами. – М.: Наука, 1982.
– 208 с.
8. Эмануэль Н.М., Кнорре Д.Г.
Курс химической кинетики. – М.: ВШ, 1984. – 463 с.