Электрический взрыв в воде

Д.т.н, профессор Христофоров Б.Д.¹, д.ф.-м.н. Христофоров О.Б.²

¹Институт динамики геосфер РАН, ²ГНЦ РФ ТРИНИТИ, Россия, Москва

Моделирование действия молнии электрическими
разрядами и излучением

Введение

Согласно [1,2], ежегодно на Земле происходит свыше 30 млрд. грозовых разрядов, которые обычно возникают внутри грозовых облаков, между ними и реже между облаком и землей или ионосферой. В отдельном грозовом облаке электрическая энергия может достигать 10¹⁰– 10¹¹ Дж, а в каждой молнии длительностью до 0.1 с, обычно выделяется энергия 10⁷- 10¹⁰ Дж (до нескольких тонн тротила). При ударе молнии в землю разряд происходит в полях около 3 кВ/см, что на порядок меньше пробойного поля для воздуха. Сначала идет лидер с током около 100 А, потом от земли обратный разряд. Эта главная стадия молнии с током до 100 кА, температурой Т ≈ 25 - 30кК и скоростью 0,1 – 0,3 от скорости света вызывает ударную волну, действие которой сопровождается громовыми раскатами. С помощью гроз реализуется взаимодействие верхних и нижних геосфер Земли путем обмена запасаемой в них механической и электрической энергии. Воздействие гроз опасно для наземных объектов и летательных аппаратов. Поэтому полезна разработка методов моделирования молнии и грома, позволяющая исследовать их действие на различные объекты и совершенствовать средства защиты от гроз.

Условия применения разрядов конденсаторных батарей для моделирования газодинамических процессов при грозах и критерии моделирования определены нами из определяющих модельные и натурные процессы МГД уравнений в [3]. Ниже приведены результаты исследований и разработки методов моделирования действия молнии и грома на различные объекты и летательные аппараты разрядом конденсаторных батарей и импульсным лазерным облучением.

Постановка модельных экспериментов

При моделировании молнии электрическим разрядом применялась батареи конденсаторов емкостью до С₀ = 13000 мкФ, напряжением до U₀= 5 кВ, запасаемой энергией до 160 кДж. При разряде батареи через плоский проводник из алюминиевой фольги или напыленного алюминия, возникал электрический взрыв, плазменное облако которого моделировало молнию, а ударная волна (УВ) гром. Разряд проводился в воздухе, на плоских преградах и конусе на входе в воздухозаборник летательного аппарата (ЛА). Применение взрывомагнитных генераторов (ВМГ) позволяло увеличить энергию разряда. Облучение преград лазерами с взрывной накачкой на длине волны 1.315 мкм позволяло увеличить плотность q подводимой энергии и параметры моделирующей плазмы. Для моделирования влияния бури на параметры УВ и плазмы при грозах разрядный промежуток и облучаемое пятно обдувались со скоростями до 500 км/с.

В опытах применялась высокоскоростная фотосъемка с разных направлений. Калориметры, фотодиоды, пироэлектрические и термопарные датчики измеряли радиационные и тепловые процессы. Пьезоэлектрические датчики и импульсомеры регистрировали газодинамические параметры плазмы и УВ. Электрический ток i, напряжение U, длительность t₀и электрическая энергия E_э разряда измерялись поясом Роговского и делителем напряжения. Для измерения параметров лазерного излучения применялся специальный измерительный комплекс.

На рис. 1 а,б,в приведены высокоскоростные фотографии разрядов у поверхности плоской преграды в режимах лупы времени и щелевой развертки, характерные для молниевой плазмы. С ростом плотности потока подводимой энергии q зона энерговыделения догоняла фронт УВ. При q ≈ 3 МВт/см² они практически совпадают.

На рис. 2 показано моделирование действия молнии на двигатели ЛА электрическим разрядом. На конусе у входа в воздухозаборник ЛА видна фольга - инициатор разряда. При лазерном моделировании излучение фокусировалось там же, где проводились разряды.

Ris_2 а,б,в

Рис.1 а, б, в. Характерные фотографии разрядного канала и его щелевые развертки у поверхности плоской преграды при плотностях потока q выделенной в разряде энергии 0,6;3; 9 МВт/см².

$C:\Users\oleg\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\Конус_2.jpg$

разряд%20на%20конусе%20МИг_ббб

Рис. 2. Фотографии двигателя ЛА (а) и электрического разряда, моделирующего действие молнии на двигатели ЛА, в различные моменты времени (б, в, г).

При разработке критериев моделирования действия молнии и грома на различные объекты электрическими разрядами и лазерным облучением применялись МГД уравнения [4], которые описывают поведение воздушной плазмы.

divB = 0; rotH = J = σ(E + uB); B = µH; rot E = - ∂B/∂t; ∂ρ/∂t + div(ρu) = 0;

P = P(ρ,e); ρ[∂u/∂t+(uÑ)u] = -ÑP+F_n; ρde/dt – (P/ρ)(dρ/dt) = j²/σ.

где E и H - напряженности электрического и магнитно поля, u – массовая скорость, e = e (P, ρ) – внутренняя энергия и уравнение состояния, ρ – плотность, F_n= J×B – пондеромоторная сила на единицу объема. Для моделирования параметров УВ применялись безразмерные критерии моделирования: π = P_m/P₀, λ = R/(E/P₀)^1/3, сI/P₀(E/P₀)^1/3, сτ/(E/P₀)^1/3, L/R. Здесь P_m/P₀ – отношение максимального давления УВ к атмосферному, E – энергия плазмы, I, τ – удельный импульс и длительность положительной фазы УВ, с- скорость звука, L, R характерный размер разряда и расстояние до него. Размерный критерий j²/σ определяет равенство удельных мощностей энерговклада в молнии и в разряде батареи. Условие (- div q) = (j²/σ) определяет равенство удельных мощностей энерговклада в лазерной плазме и молнии, где j – плотность тока, σ - проводимость плазмы, q – плотность потока поглощенной в плазме энергии излучения. Полученные критерии позволяют по данным модельных экспериментов и расчетов определить действие гроз на различные объекты.

Результаты модельных исследований параметров УВ и плазменного факела

Некоторые результаты измерений параметров УВ и плазменного факела при разрядах и лазерном облучении приведены в таблицах и на рисунках. На рис. 3,4 показаны результаты измерений и расчетов безразмерных зависимостей ∆π (λ ) максимального давления и приведенного удельного импульса I/E^1/3 (λ ) в сферической УВ от безразмерного расстояния. Светлыми и черными ромбами показаны результаты измерений при лазерном облучении и разрядах. Сплошными и пунктирными линиями показаны расчеты Brode для взрыва тротила и нагретой сферы [3,5].

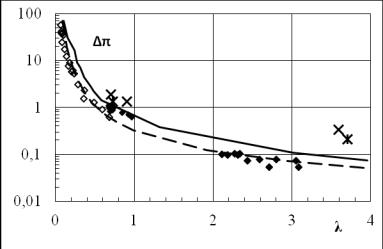Рис.3. Зависимости приращения безразмерного давления ∆π на фронте сферической УВ от приведенного расстояния λ при взрывах в воздухе. Сплошными и пунктирными линиями показаны расчеты Brode для взрыва тротила и нагретой сферы [3,5]. Светлые и черные ромбы - измерения при лазерном облучении и разрядах. Большие кресты и звезды измерения при скорости обдува 80 и 40 % от максимальной при разрядах.

Зависимости ∆P_m (R/G^1/3) и I/G^1/3от R/G^1/3описываются формулами Садовского, совпадающими с расчетами Броуда при R/G^1/3>1, которые для тротила имеют вид

∆P_m= 0,084/(R/G^1/3) + 0,27/(R/G^1/3)² + 0,695/(R/G^1/3)³, I =184//(R/G^2/3) (1),

где давление ∆P_m в МПа, расстояние R в м, G масса тротила в кг [3,5]. Теплота взрыва тротила принята Q = 4,2 МДж/кг, E= GQ, R/G^1/3 = 3,47λ =3,47R/(E/P₀)^1/3.

При сравнении расчетов параметров УВ при взрывах с измерениями при разрядах на плоских преградах, выделившаяся энергия полагалась равной E = 2(E_э – E_e), а при разрядах на конусе E = 1,75(E_э– E_e), где E_э – энергия разряда, E_e = 3кДж/г - энергия нагрева фольги инициатора разряда до пробоя воздуха. При лазерном облучении плоскости и конуса энергия взрыва в воздухе полагалась соответственно равной E = 2E_л и E = 1,75E_л, где E_л – энергия лазерного излучения, поглощенная в плазме.

Средние значения тротилового эквивалента разряда ТЭ = 0,27 и 0,34 для максимального давления и импульса получены сравнением результатов измерений с расчетами по формулам (1) для взрыва тротила. При сравнении с расчетами для взрыва горячей сферы, практически совпавшими с опытными данными, ТЭ = 1. Измерения параметров УВ при внешнем обдуве приведенные на рис. 3 (кресты и звездочки) для моделирования влияния бури на интенсивность грозы показали, что при скоростях обдува выше 100 м/с давление возрастает более, чем вдвое, а ТЭ на порядок.

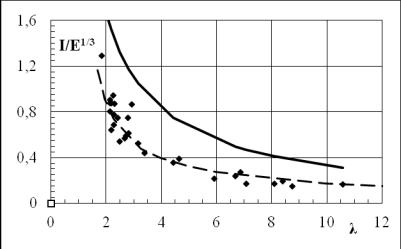Рис. 4. Зависимости приведенного удельного импульса I/E^1/3 в сферической УВ от приведенного расстояния λ. Сплошные и пунктирные линии - расчеты по формулам Броуда для взрывов тротила и горячей сферы [3,5]. Ромбы– измерения при электрическом разряде.

В таблице 1 приведены некоторые результаты измерений параметров разрядной и лазерной плазмы на конусе ЛА в 10 см от входа в воздухозаборник, где E - полная энергия плазмы с учетом энергии горения фольги, V - объем факела, m - масса фольги, h высота подъема факела на преграде, I – удельный импульс, переданный преграде. T_я,ик- яркостная температура плазмы в ИК области.

Таблица 1. Характерные параметры разрядной и лазерной и плазмы после окончания выделения энергии.

	Разрядная плазма					Лазерная плазма
№	46	47	60	50	49	1	2	3	4
E, кДж	35	27	16,6	19	14	23	19,5	18	30
E_э, кДж	31	22,7	16,4	15	10,4	-	-	-	-
m, г	0,14	0,14	0,005	0,14	0,14	-	-	-	-
h, см	21	18	--	14	11,5	-	-	11,5	21
V₁, л	52	42	-	26	20	31	29	-	-
T_я,ик,кК	27,5	21	-	22	21	-	-	-	32
I, Пас	5	3,5	-	2,8	2,1	3,9	2,5	3,2	5,4

Параметры разрядной плазмы зависят от массы m фольги - инициатора разряда. Объемы плазмы V₁на конусе после окончания разряда можно описать эмпирической формулой V₁/E_э= 0,91+29 m/E_э. При m/E_э~ 0 измеренная доля энергии излучения E_и/E_э = 0,4 - 0,5. При больших m/E_эизлученная энергия могла превышать энергию разряда (E_и/E_э >1). В среднем, увеличение объема плазмы за счет горения фольги около 30 л/г Баланс энергии для используемых разрядников можно написать в виде E = E_э + E_гор = E_ув + E_и + ∆E_г, где E_э и E_гор выделившаяся энергии электрического тока и горения, E_ув - энергия уносимая УВ, E_и - энергия излучения, ∆E_г энергия нагретого газа при атмосферном давлении. Приращение энергии газа в факеле после прекращения его свечения оценено из соотношения ∆E_г = P₀V₁/(k₁-1) - P₀V₁/(k₀-1) = 2,5 P₀V₁. При k₁ = 1,2; P₀ = 0,1 МПа, ∆E_г/E_э= 2,5 P₀(0,91+29 m/E_э) = 0,23+7,2 m/E_э.

Проведенные измерения показали, что при m/E_э> 4 10^-3г/кДж. E_ув = 0,35(E_э – E_e) = 0,35E_э –1,05 m, где E_e/m = 3кДж/г, энергия газа в факеле после высвета ∆E_г = 0,23+7,2 m, энергия излучения E_и = 0,53+19 m. E = 1,1 E_э+21 m. При m/E_э< 4 10^-3г/кДж, E_и = 0,45+37 m, E = E_э + E_гор = E_ув + E_и + ∆E_г = 1,03 E_э+38,3 m. При этом, когда m = 0, E = 1,03E_э баланс энергии выполнялся с точностью превышающей погрешность экспериментов. При m = 0 баланс энергии для разряда должен быть близок к балансу при воздействии молнии, для которой принималось E_ув /E_м = 0,35, ∆E_г/E_м = 0,23, E_и /E_м = 0,45, где E_м – энергия молнии.

При лазерном воздействии, где не было влияния горения и пондермоторных сил параметры молниевой плазмы воспроизводились точнее. Различия между параметрами лазерной и разрядной плазмы при m =0 с одинаковой энергией были в пределах погрешности измерений. При этом баланс энергии был близок к характерному для молнии, когда E_ув / E_м = 0,35, ∆E_г/ E_м = 0,23, E_и /E_м = 0,45, если энергия излучения лазера E_л поглощенная в плазме равнялась энергии E_м выделившейся в молнии.

Моделирование действия молнии на двигатели летательных аппаратов

Удар молнии на входе в воздухозаборник ЛА может вызвать помпаж, потерю газодинамической устойчивости и прекращение работы двигателя ЛА. Время срабатывания применяемых антипомпажных систем может превышать необходимое для их без аварийной работы. В связи с этим, проведены модельные исследования воздействия молнии на газотурбинные двигатели в списанных ЛА типа МИГ- 21 при разных частотах работы двигателя n от 0 до 93 % от максимальной частоты.

В опытах плазма создавалась разрядом или лазерным облучением конуса перед входом в ВЗ двигателя ЛА. Измерялись параметры плазмы перед и внутри ВЗ, а также условия нарушения газодинамической устойчивости двигателя при разных режимах его работы. Схема модельных экспериментов показана на рис. 2 а, б. В таблице 2 приведены параметры разрядной и лазерной плазмы затекающей в ВЗ, где E – начальная энергия плазмы, ∆P_0,5, ∆P₃ и ∆P_6,4– приращение давления УВ в области нагретого газа в ВЗ на расстояниях 0,5; 3 и 6,4 м от места воздействия, t_пр – время прихода УВ к датчику, L и U - длина и скорость области нагретого газа, ∆T_{м 6,4}, ∆T_{ср 6,4} – максимальная и средняя температуры области нагретого газа на расстоянии 6,4 м от разряда.

Таблица 2. Параметры разрядной и лазерной и плазмы внутри воздухозаборника ЛА с работающим двигателем.

	Разрядная плазма					Лазерная плазма
№	46	47	60	50	49	1	2	3	4
E, кДж	35	27	16,6	19	14	23	19,5	18	30
m, г	0,14	0,14	0,005	0,14	0,14	-	-	-	-
∆P_0,5, МПа	0,2	0,22	-	0,4	0,17	0,17	0,14	-	0,17
t_пр, мс	1	1	-	0,95	1	1	1,1	-	-
∆P₃, МПа	0,04	0,037	-	0,036	-	0,045	-	-	0,067
t_пр, мс	6	6	-	5,6	-	5,9	-	-	5,4
∆P_6,4, МПа	0,01	0,01	-	-	0,009	0,012	-	-	0,013
t_пр, мс	13,2	12,6	-	-	15	13	-	-	12
L, м	1,5	1,6	-	1,45	1,5	1,1	1,25	1,45	1,3
U, м/с	130	157	-	150	157	146	153	152	170
∆T_м_6,4,K	53	68	-	78	35	48	82	44	85
∆T_ср_6,4, K	30	34	-	29	19	27	50	20	60

В опытах с подчеркнутыми значениями энергии происходил помпаж (заглохание) двигателя. При минимальной энергии разрядной плазмы E = 14 кДж нарушений в работе двигателя не наблюдалось. Энергия ∆E_г нагретого газа втекающего в ВЗ соответствовала полученной предварительно из эмпирических формул ∆E_г = 0,23 E_л и ∆E_г = 0,23 E_э+7,2m при лазерном облучении и электроразряде.

Проведенные модельные опыты показали, что при воздействии молнии с энергией E_м до 50 кДж параметры УВ не влияют на условия нарушения газодинамической устойчивости в работе двигателя. Срыв в его работе наступал значительно позже прихода УВ и лишь после прохождения области нагретого газа. Условия нарушения ГДУ двигателя зависели лишь от параметров области нагретого газа и числа оборотов двигателя. Минимальные приращения максимальной температуры области нагретого газа у компрессора, при которой могла нарушаться работа двигателя составляли ∆T_м
6,4 = 42 К. При ∆T_{м 6,4} = 75 К нарушения работы ГТД наблюдались всегда. Нарушения в работе двигателя сопровождались выбросом нагретого газа навстречу потоку в ВЗ, который регистрировался тепловыми датчиками после прохождения области нагретого газа через компрессор и из сопла ЛА, который регистрировался фотокамерами. Нарушения ГДУ двигателя носили вероятностный характер и определялись объемом или энергией области нагретого газа поступавшего в ВЗ. С ростом скорости продувки необходимая энергия нагретого газа уменьшалась. Отмечено уменьшение потерь энергии нагретого облака на стенки ВЗ при росте частоты работы двигателя и скорости продувки из-за уменьшения теплопередачи на стенки. Проведенные опыты с моделированием воздействия молнии при полете ЛА на низких высотах с дозвуковыми скоростями проводились при обдуве испытуемого ЛА со скоростями до 500 км/час.

Определение параметров гроз по данным модельных исследований

В настоящее время опубликовано большое количество фотографий молний с диаметром, светящегося канала с температурой около 3 кК от 0,1 до 1 м, по которым можно оценить их энергию.

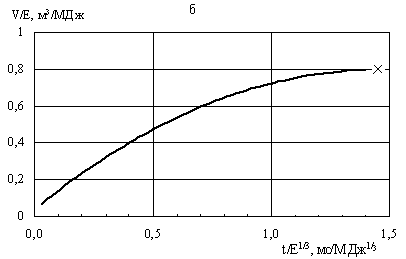
На рис. 5 приведена зависимость приведенного объема V/Eот приведенного времени t/E^1/3ограниченного изотермой T/T₀= 10 (T₀ = 300 К) при взрыве горячей сферы [3,5], по которой оценивалась энергия молнии. Крест - приведенный эквивалентный объем молнии V₁/E = 0,8 м³/МДж, принятый равным максимальному удельному объему молнии ограниченному изотермы. V₁ = π R₁²×h = 3,8м³при радиусе R₁= 1,1м участка высотой h = 1м для цилиндрической симметрии. Удельная энергия молнии E = 4,75 МДж/м. Время от начала разряда t = 2,08 мс. Молния с характерной длиной 4 км будет иметь энергию E = 4,75× 4000 = 19000 МДж или около 4500 кг тротила. При радиусе R₁ = 5 см энергия молнии будет около 40 МДж или почти в 500 раз меньше.