Технические науки / 6.Электротехника и радиоэлектроника.

к.т.н. Боннет В.В., Прудников А.Ю.,

к.т.н. Потапов В.В., к.т.н. Черных А.Г.

Иркутский государственный аграрный университет, Россия

АЛГОРИТМ СИНТЕЗА РАСЧЕТНОЙ МОДЕЛИ ПРИ ЭКСЦЕНТРИСИТЕТЕ АСИНХРОННОГО ДВИГАТЕЛЯ

Влияние геометрии воздушного зазора асинхронного электродвигателя (АД) на его электромагнитное состояние можно оценить с использованием соответствующих алгоритмов, позволяющих проанализировать доступные для измерения сигналы, полученные на стороне двигателя без вмешательства в его текущую работу. Таким сигналами являются токи и напряжения питающих цепей фаз статора и скорость двигателя.

В практике математического моделирования электромеханических процессов АД в динамических режимах работы, с точки зрения синтеза модели на основе измеряемых физических величин, используется расчетная модель двухфазной обобщенной электрической машины [1].

Применительно к АД его расчетная модель (РМ) состоит из цилиндрического статора и ротора, снабженных двумя концентрическими слоями обмоток (рис. 1).

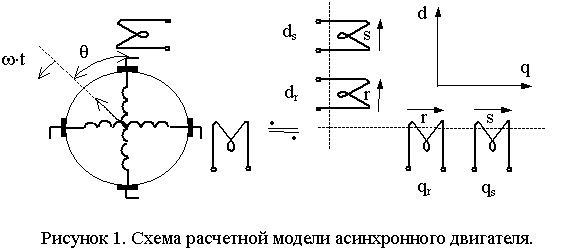
При этом по аналогии с обобщенной моделью двухфазной машины, на статоре слой обмотки представляется двумя катушками: одной – на магнитной оси обмотки какой-либо фазы (продольная ось – d_s) и другой – помещенной под прямым углом к первой (продольная ось – q_s). На роторе слой обмотки представляется в виде замкнутой барабанной обмотки, на которой размещены две пары щеток: одна – по магнитной оси (продольная ось – d_r), другая – под прямым углом к первой (поперечная ось – q_r).

Введем обозначения: – напряжение на обмотке ;– напряжение на обмотке ;– напряжение на обмотке ;– напряжение на обмотке ; – ток в обмотке ; – ток в обмотке ; – ток в обмотке ;– ток в обмотке ;

активное

; q – угол поворота вала ротора; – угловая скорость вращения ротора; – момент импульса; – активный момент.

В расчетной модели АД (рис. 1) воздушный зазор между ротором и статором равномерный и магнитная цепь по осям d и q симметрична, от угла поворота ротора q зависят лишь взаимные индуктивности пар обмоток. В этом случае магнитный поток, сцепленный с парой обмоток, изменяется по косинусоидальному закону

.

Так как, в РМ пары обмоток или параллельны или перпендикулярны, т.е. q=0 или q=90^° , то очевидно, что трансформаторная э.д.с будет наводиться в обмотках соосных.

В свою очередь генерированные э.д.с. (²вращения²) имеют в качестве коэффициента

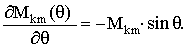
Последние выражение показывает, что э.д.с. вращения будет наводиться в том случае, если взаимная индуктивность минимальна, т.е. когда обмотки взаимно перпендикулярны. Если за положительное направление вращения принять вращение против хода часовой стрелки (в направлении от оси q к оси d), то коэффициент пропорциональности будет отрицательный равный ( M_qd), при вращении от оси d к оси q положительный равный (+ M_dq).

С учетом введенных обозначений и приведенных замечаний уравнения электромеханического равновесия для РМ примут вид

Учитывая, что в РМ статор и ротор являются гладкими уравнения (1) ¸ (4) могут быть упрощены, принимая во внимание, что

Одновременно необходимо учитывать, что поскольку физические обмотки статора АД являются трехфазными, то необходимо определяющие их электрические параметры соотнести с электрическими параметрами обмоток РМ, т.е. выразить через параметры, введенные в уравнениях (6) ¸ (8).

Пусть Т-образная схема замещения АД представлена участками с сосредоточенными параметрами, включающими:

– катушку индуктивности с сопротивлением x₁ (реактивное сопротивление рассеяния статорной обмотки), напряжение на которой равно реактивной составляющей падения напряжения в фазе статора АД;

– участок с сопротивлением r₁ (активное сопротивление фазы статора), напряжение на котором равно активной составляющей падения напряжения в фазе статора АД;

– катушку индуктивности с сопротивлением x₂^/ (реактивное сопротивление ротора, приведенное к статорной цепи), напряжение на которой равно реактивной составляющей падения напряжения в фазе ротора АД;

– участок с сопротивлением r₂^/ (приведенное активное сопротивление ротора), напряжение на котором равно активной составляющей падения напряжения в фазе ротора АД;

– катушку индуктивности с сопротивлением x₀, ток через которую I_0r определяет реактивную составляющую тока холостого хода I₀;

– участок с сопротивлением r₀, ток через который I_0a определяет активную составляющую тока холостого хода I₀.

В справочниках, как правило, приводятся в относительных единицах расчетные значения параметров упрощенной Г-образной схемы замещения для рабочей ветви: активного сопротивления R₁^/ и индуктивного сопротивления рассеяния X₁^/ обмотки статора; приведенных к обмотке статора активного сопротивления R₂^// и индуктивного сопротивления рассеяния X₂^// обмотки ротора, а так же главного индуктивного сопротивления X_m – для ветви намагничивания.

Активное R₁ и индуктивное X₁ сопротивления ветви намагничивания Г-образной схемы замещения определяются выражениями

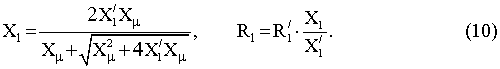
Принимая во внимание соотношения (10) параметры Т-образной схемы замещения равны

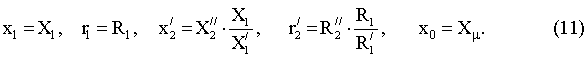
Окончательно, для принятых в выражениях (6) ¸ (8) обозначений, активные сопротивления и индуктивности обмоток РМ выраженные через параметры Т-образной схемы замещения (11) примут вид

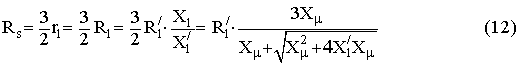
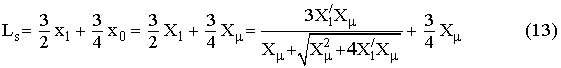
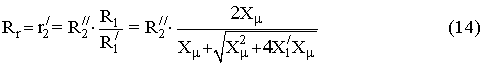
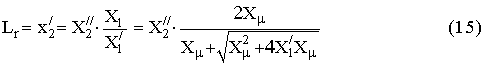
Для того чтобы в выражениях (12) ¸ (16) перейти от относительных значений к физическим с использованием базисных величин сопротивления Z_Б и частоты w_Б необходимо воспользоваться следующими соотношениями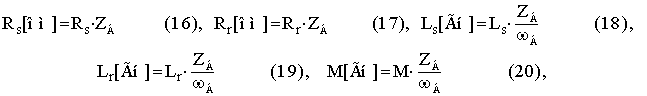

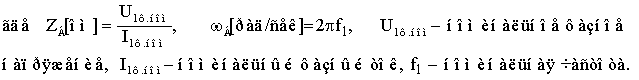
Выражения (12) ¸ (16) позволяют вычислить активные сопротивления и индуктивности обмоток РМ при условии, что мгновенное значение радиальной составляющей индукции в воздушном зазоре для основной гармоники определяется выражением [2]

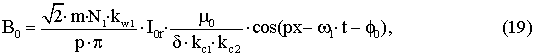
_{где m – число фаз; N1 – число витков в обмотке статора; kwl – обмоточный коэффициент для основной волны; p – число пар полюсов; I0r – реактивная составляющая тока холостого хода; d – длина воздушного зазора; kc – коэффициент Картера, учитывающий зубчатость статора kc1 и ротора kc2; m0 – магнитная постоянная (плотность магнитного потока в вакууме); x=wx·t – текущая угловая координата рассматриваемой точки в воздушном зазоре (рад); w1 – угловая частота основной волны питающего напряжения; f0 – угол сдвига фаз в режиме холостого хода.}

Выражение (19) можно упростить, если учесть, что для РМ p=1 и положить w_х = w₁. Тогда

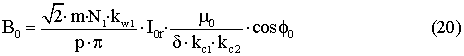
Таким образом, если текущая угловая координата x рассматриваемой точки в воздушном зазоре связана с системой координат вращающейся с угловой частотой основной волны питающего напряжения (w_х = w₁), то B₀ =const и, как следствие, параметры обмоток в уравнениях (6) ¸ (8), не будут являться функциями времени. При этом уравнения (1) ¸ (5) в ортогональных осях (a,b), вращающихся с угловой скоростью w₁ по отношению к ортогональной неподвижной системе координат (d,q) примут вид

Необходимо отметить, что левые части уравнений (21) ¸ (24) являются постоянными величинами, удовлетворяющие соотношениям

Уравнения (21) ¸ (25) с учетом начальных условий (26) могут быть преобразованы к виду

В АД мощностью 1,1¸7,5 кВт относительная величина падения напряжения в фазе обмотки статора DU_1ф.ном » 0,06 ¸ 0,04 U_1ф.ном. Тогда величина э.д.с E_1ф » 0,94 ¸ 0,96 U_1ф.ном, а E_1ф.max прямо пропорциональна максимальному значению B_0.max радиальной составляющей индукции в воздушном зазоре для основной гармоники вычисленному по выражению (20).

Для пространственной гармоники учитывающей эксцентриситет с порядковым номером i=1 вращающейся в направлении основной гармоники, мгновенное значение радиальной составляющей индукции в воздушном зазоре равно [2]

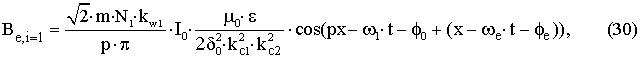
Деление амплитудных значений выражений (30) и (19) дает тождество

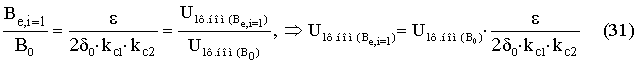
Определим угловую скорость вращения w_хe,i=1 ортогонального базиса (a,b)_e,i=1 по отношению к ортогональной неподвижной системе координат (d,q), используя аргумент функции выражения (30), получим

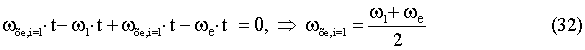
С учетом (31) и (32) выражения (16) ¸ (20) определятся соотношениями

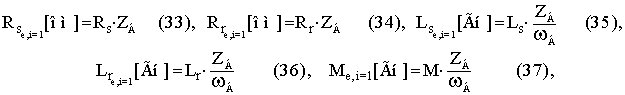
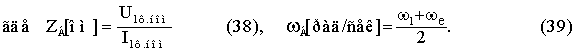
Принимая во внимание тождества (33) ¸ (39) система уравнений электромеханического равновесия РМ АД учитывающей эксцентриситет для пространственной гармоники индукции с порядковым номером i=1 вращающейся в направлении основной гармоники, по аналогии с (27) ¸ (29) запишется в виде системы уравнений

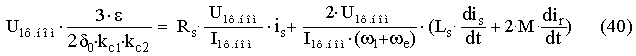
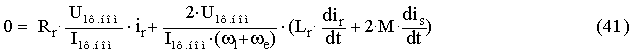
Если пространственная гармоника учитывающая эксцентриситет имеет порядковый номер i=-1, т.е. вращается против направления вращения основной гармоники, то мгновенное значение радиальной составляющей индукции в воздушном зазоре равно [2]

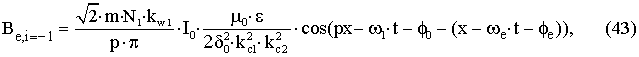
В этом случае при p=1, имеем n_e=1-1/p=0, т.е. пространственная гармоника с порядковый номер i=-1 отсутствует как составляющая результирующей индукции в воздушном зазоре рассматриваемой РМ.

Литература:

1. 1. Бондаренко, А.В. Приведение параметров эквивалентных обмоток экранированной асинхронной машины к параметрам расчетной схемы замещения / А.В.Бондаренко, Ю.П. Коськин, А.Г. Черных // Вестник ИрГСХА: Сборник научных трудов / ИрГСХА. – Иркутск, 2010. – Вып. 41 – С. 107 ¸ 116.

2. Боннет, В.В. Определение магнитодвижущей силы и магнитной проницаемости воздушного зазора при эксцентриситете асинхронного двигателя / В.В. Боннет, А.Ю. Прудников, В.В. Потапов, А.Г. Черных// Materiály XI mezinárodní vědecko - praktická konference «Vědecký průmysl evropského kontinentu – 2015»/Díl 11. Technické vědy.Moderní informační technologie.Matematika.: Praha. Publishing House «Education and Science» – С. 43 ¸ 51.