Экономика

варианты расчета объем ЭКОНОМИЧЕСКой ОБОЛОЧКИ

Пиль Э.А.

Академик РАЕ, профессор, доктор технических наук,

г. Санкт-Петербург

В статье описана экономическая оболочка, которую можно представить в виде объема сферы. Данный объем можно представить как валовой внутренний продукт (ВВП) страны. Показаны виды деформации сферы под воздействием внешнего и внутреннего давления.

Ранее в своих статьях автор показал, что ВВП любой страны можно представить как сферическую оболочку, а точнее площадь ее поверхности [1, 2, 3, 4].

Валовой внутренний продукт представляет собой макроэкономический показатель, отражающий рыночную стоимость всех конечных товаров и услуг, произведенных за год во всех отраслях экономики на территории государства для потребления, экспорта и накопления, вне зависимости от национальной принадлежности использованных факторов производства. То есть, его можно представить совокупностью конечных товаров и услуг предприятий (компаний), следовательно, каждое предприятие (компания) является отдельной ее частью площади сферы.

При этом объем экономической сферы можно классифицировать на два класса (рис. 1):

1. первый класс - объем экономической сферы представляет собой замкнутую сферу без трещин V_sc;

2. второй класс - объем экономической сферы представляет собой разомкнутую сферу V_so, у которой, как минимум, две грани двух пирамид не соприкасаются между собой, т.е. имеется трещина.

В свою очередь каждый класс подразделяется на следующие десять одинаковых подклассов:

1. Построенный объем экономической сферы V_s представляет собой совокупность отдельных, одинаковых пирамид одинакового объема V_pi и одинакового радиуса R_р_i;

2. Построенный объем экономической сферы V_s представляет собой совокупность отдельных, одинаковых пирамид разного объема V_pi и одинакового радиуса R_pi;

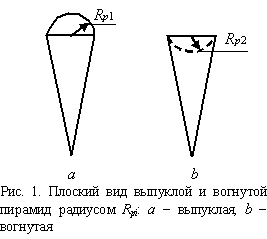
3. Построенный объем экономической сферы V_s представляет собой совокупность отдельных, выпукло-вогнутых одинаковых пирамид одинакового объема V_pi и с постоянными радиусами R_pi для выпуклых R_p₁ и вогнутых R_p₂пирамид. На рис. 1 представлены два плоских изображения выпуклой и вогнутой пирамид;

4. Построенный объем экономической сферы V_s представляет собой совокупность отдельных, выпукло-вогнутых одинаковых пирамид одинакового объема V_pi, с постоянными и переменными радиусами R_pi (для выпуклых пирамид постоянный радиус R_p₁, а для вогнутых пирамид переменные радиусы R_p₂);

5. Построенный объем экономической сферы V_s представляет совокупность отдельных, собой выпукло-вогнутых одинаковых пирамид одинакового объема V_pi, с переменными и постоянными радиусами R_pi (для выпуклых пирамид переменные радиусы R_p₁, а для вогнутых пирамид постоянный радиус R_p₂);

6. Построенный объем экономической сферы V_s представляет собой совокупность отдельных, выпукло-вогнутых одинаковых пирамид одинакового объема V_pi и с переменными радиусами R_pi (для пирамид переменные радиусы R_p₁, а для вогнутых пирамид постоянный радиус R_p₂);

7. Построенный объем экономической сферы V_s представляет собой совокупность отдельных, выпукло-вогнутых одинаковых пирамид с переменными объемами V_pi и одинаковыми радиусами R_pi (для выпуклых пирамид радиус R_p₁, а для вогнутых пирамид радиус R_p₂);

8. Построенный объем экономической сферы V_s представляет собой совокупность отдельных, выпукло-вогнутых одинаковых пирамид с переменными объемами V_pi и разными радиусами R_pi (для выпуклых пирамид постоянный радиус R_p₁, а для вогнутых пирамид переменный радиус R_p₂);

9. Построенный объем экономической сферы V_s представляет собой совокупность отдельных, выпукло-вогнутых одинаковых пирамид с переменными объемами V_pi и разными радиусами R_pi (для выпуклых пирамид переменный радиус R_p₁, а для вогнутых пирамид постоянный радиус R_p₂);

10. Построенный объем экономической сферы V_s представляет собой совокупность отдельных, выпукло-вогнутых одинаковых пирамид с переменными объемами V_pi и переменные радиусами R_pi (для выпуклых и вогнутых пирамид переменные радиусы R_p₁ и R_p₂).

Рассмотрим теперь отдельно, представленные выше подклассы.

Подклассы без трещин:

1. Построенный объем экономической сферы V_s представляет собой совокупность отдельных, одинаковых пирамид одинакового объема V_pi и одинакового радиуса R_р_i.

Этот подкласс представляет собой обычную сферу, построенную из одинаковых пирамид. Минимальное количество граней пирамиды равно трем, т.е. n_f_min = 3, а максимальное количество равно n_f_max, т.е. n_f = n_f_max. Так как мы рассчитываем объем пирамиды, следовательно, количество ее граней должно соответствовать количеству переменных n_ВВП, которые используются при расчете ВВП страны. Таким образом, можно записать следующие границы для количества граней пирамид, в которых они могут существовать 3 £ n_f £ n_ВВП. При этом объемы пирамид равны между собой V_p₁ = V_p₂…= V_pi.

2. Построенный объем экономической сферы V_s представляет собой совокупность отдельных, одинаковых пирамид разного объема V_pi и одинакового радиуса R_pi. Следовательно, можно записать для объемов V_p₁ ¹ V_p₂…¹ V_pi. Так как радиусы одинаковы для выпуклой R_p₁ и вогнутой R_p₂ пирамид, можно записать следующее равенство R_p₁ = R_p₂.

3. Построенный объем экономической сферы V_s представляет собой совокупность отдельных, выпукло-вогнутых одинаковых пирамид одинакового объема V_pi и с постоянными радиусами R_pi для выпуклых R_p₁ и вогнутых R_p₂ пирамид. Таким образом, здесь можно записать для объемов пирамид выражение V_p₁= V_p₂…= V_p_i, а для их радиусов R_p₁ = R_p₂.

5. Построенный объем экономической сферы V_s представляет собой совокупность отдельных, выпукло-вогнутых одинаковых пирамид одинакового объема V_pi, с переменными и постоянными радиусами R_pi (для выпуклых пирамид переменные радиусы R_p₁, а для вогнутых пирамид постоянный радиус R_p₂). В этом подклассе V_p₁ = V_p₂, R_p₁₁ ¹ R_p₁₂, а R_p₂₁ = R_p₂₂ =…R_p₂_i = const.

6. Построенный объем экономической сферы V_s представляет собой совокупность отдельных, выпукло-вогнутых одинаковых пирамид одинакового объема V_pi и с переменными радиусами R_pi (для выпуклых пирамид переменные радиусы R_p₁, а для вогнутых пирамид переменные радиусы R_p₂). Следовательно, V_p₁ = V_p₂, R_p₁₁ ¹ R_p₁₂, R_p₂₁ ¹ R_p₂₂.

Здесь радиусы для выпуклой R_p₁ и вогнутой R_p₂ пирамид могут быть разбиты на следующие две группы:

· все радиусы выпуклой R_p₁ и вогнутой R_p₂ пирамид равны между собой, т.е. R_p₁₁ = R_p₁₂ =…R_p₁_i = R_p₂₁= R_p₂₂ =…R_p₂_j;

· все радиусы выпуклой R_p₁ и вогнутой R_p₂ пирамид равны между собой только в своих группах, т.е. R_p₁₁ = R_p₁₂ =…R_p₁_i и R_p₂₁= R_p₂₂ =…R_p₂_j, следовательно, R_p₁_i ¹ R_p₂_j.

К описанным выше 10 вариантам замкнутой экономической сферы приемлемы три формулы для расчета ее объема:

1. Для первых двух вариантов, когда экономическая сфера представляет собой совокупность объемов отдельных пирамид с плоским основанием, используется формула (1).

где: V_p₁, V_p₁…V_pi − объемы отдельных пирамид, ед.³.

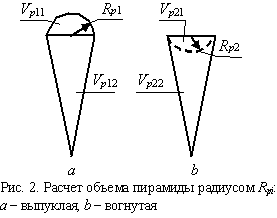
Для выпукло-вогнутых пирамид, радиусом R_pi, расчеты производят по формулам 2 и 3 (рис. 2);

Для выпуклых пирамид

V_p₁ = V_p₁₁ + V_p₁₂, (2)

где: V_p₁₁ - объем выпуклого сегмента рассматриваемой пирамиды, ед.³;

V_p₁₂ - объем пирамиды, ед.³.

Для вогнутых пирамид

V_p₂ = V_p₂₂ - V_p₂₁, (3)

где: V_p₂₁ - объем вогнутого сегмента рассматриваемой пирамиды, ед.³;

V_p₂₂ - объем пирамиды, ед.³;

Аналогичные описания распространяются и на подкласс разомкнутых сфер, имеющих хоть одну трещину, т.е. когда две грани двух пирамид не соприкасаются между собой.

Если появится необходимость превратить любую экономическую сферу из разомкнутой, т.е. с трещиной (трещинами), в замкнутую, то это можно осуществить следующим путем. Надо взять за основу равностороннюю единичную экономическую пирамиду с длиной стороны основания l_sp равной единице (l_sp₁ = 1), площадь которого обозначим как S_pht₁. Длина боковой грани данной пирамиды l_f также равна единице (l_f = 1).

На основе этого, введем здесь понятие “единичного теоретического объема” экономической пирамиды V_pht, где длина каждой стороны основания пирамиды l_sp и длина боковой ее грани l_f равны единице, ед.³. Здесь имеется ввиду пирамида, которая не подверглась воздействию давления.

Теперь сделаем следующее преобразование, все стороны рассматриваемой пирамиды увеличим (уменьшим), в зависимости от их размеров, так, чтобы длины сторон основания и грани были равны единице. Таким образом, мы приведем все пирамиды, из которых состоит экономическая оболочка к единичному теоретическому объему V_pht₁. В этом случае получится теоретическая экономическая оболочка V_pht, состоящая из совокупности единичных объемов экономических пирамид V_pht₁_n. Исходя из этого, объем теоретической экономической оболочки V_pht можно рассчитать по формуле (4)

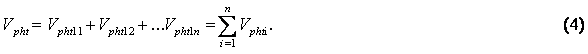
Следующим шагом введем коэффициент увеличения (уменьшения) стороны основания пирамиды l_sp и обозначим его как K_sp. Применение этого коэффициента позволяет нам привести любую сторону основания пирамиды l_sp к значению единице, т.е. l_sp₁ = 1, т.е. к равностороннему многограннику. Аналогичный коэффициент K_spb применим для граней пирамид. Таким образом, значения l_sp₁, l_f₁ и h_sp₁ можно рассчитать по формулам 5 и 6 соответственно, т.е. привести все переменные пирамиды к единице

Величина этих коэффициентов всегда больше нуля (K_sp > 0, K_spb > 0). При этом если значения коэффициентов K_sp и K_spb лежат в следующих границах 0 < K_sp < 1 и 0 < K_sbp < 1, то, следовательно, рассматриваемая сторона основания l_sp и грани l_f пирамиды уменьшаются, т.к. их значения больше единице. Если же значения коэффициента K_sp и K_spb больше единице, т.е. K_sp > 1 и K_spb > 1 это означает, что сторона основания l_sp и грани l_f пирамиды лежат в границах 0 < l_sp < 1 и 0 < l_f < 1. Когда эти коэффициенты равны единице (K_sp = K_spb = 1) это означает, что сторона основания l_sp и грани l_f пирамиды равны единице (l_sp = l_f = 1). Здесь, естественно, возможны варианты, когда эти коэффициенты имеют разные значения, например, K_sp > 1, а K_spb < 1 или K_sp = 1, а K_spb > 1.

Ввиду того, что количество пирамид в сферической экономической оболочке может быть большое количество, если рассчитывается ВВП страны, то следует использовать соответствующую таблицу 1, образец которой представлен ниже.

Таблица 1. Приведение значений всех длин сторон l_sp и граней l_f треугольной пирамиды к единице

№

п/п

l_sp

K_sp

l_sp

K_sp

l_sp

K_sp

l_f

K_spb

l_f

K_spb

l_f

K_spb

l_sp₁₁

K_sp₁₁

l_sp₁₂

K_sp₁₂

l_sp₁₃

K_sp₁₃

l_f₁₁

K_spb₁₁

l_f₁₂

K_spb₁₂

l_f₁₃

K_spb₁₃

l_sp₂₁

K_sp₂₁

l_sp₂₂

K_sp₂₂

l_sp₂₃

K_sp₂₃

l_f₂₁

K_spb₁₂

l_f₂₂

K_spb₂₂

l_f₂₃

K_spb₂₃

…

l_spi₁

K_spi₁

l_spi₂

K_spi₂

l_spi₃

K_spi₃

l_fi₁

K_spbi

l_fi₂

K_spbi

l_fi₃

K_spbi

В табл. 1 представлен пример приведения значений всех трех переменных в пирамиде l_sp и l_f к единице за исключением, когда их значения равны единице, т.к. в этом случае значения коэффициентов будут следующие: K_sp = 1 и K_spb= 1. Здесь номер порядковый номер (№ п/п) соответствует номеру рассматриваемой пирамиды.

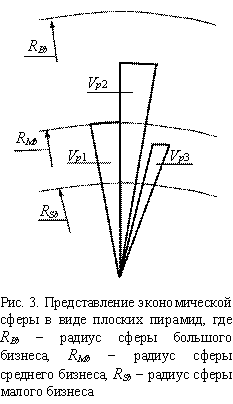
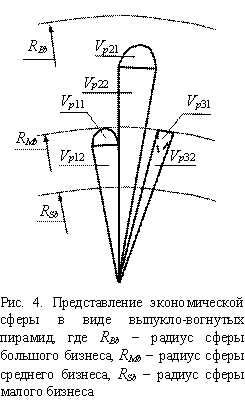
При расчете объема сферической экономической оболочки целесообразно представлять ее в виде совокупности плоских пирамид, как это сделано на рис. 3, чем в виде выпуклых или вогнутых пирамид, представленных на рис. 4. При этом, как видно из рисунков 3 и 4, эти пирамиды разомкнутые, т.к. пирамиды 2 и 3 не соприкасаются гранями друг с другом.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. Пиль Э.А. Виды деформации экономической оболочки под воздействием различных сил // Вестник ИНЖЭКОНа. Серия «Экономика» №4 (17), 2007 – С.226 – 231

2. Пиль Э.А. Применение теории и оболочек для описания процессов, происходящих в экономике // Альманах современной науки и образования. 2009. №3. С. 137-139.

3. Пиль Э.А. Влияние различных переменных на экономическую оболочку страны // Альманах современной науки и образования. 2012. №12 (67). С. 123-126

4. Pil E.A. Влияние шести переменных на расчет ВВП // Materials of the XII International research and practical conference, «Modern European science – 2016», June 30 - July 7, 2016 Volume 3. Economic science. Public administration, Political science. Sheffield. Science and education. LTD. UK – 108 p. – С. 23–26