СЫҒЫЛҒАН БЕЙНЕЛЕР ПРИНЦИПІ ЖӘНЕ ИНТЕГРАЛ ТЕҢДЕУ ҰҒЫМЫ

Абдуллаева Айнур Мешитбаевна аға оқытушы, магистр

«Ақмешіт» гуманитарлық-техникалық институты

Алтинбаева Жанат Есенбековна математика пәнінің мұғалімі

С.Әлжіков атындағы №144 орта мектебі

Алгебралық немесе дифференциал теңдеулердің шешулерінің бар болуы және жалғыздығы жөніндегі көптеген мәселелерді метрикалық кеңістікті өзіне өзін бейнелеу кезіндегі қозғалмайтын нүктенің бар болуы және жалғыздығы жөніндегі мәселе ретінде тұжырымдауға болады. Толық метрикалық кеңістіктегі бейнелер үшін қозғалмайтын нүктенің бар болуы мен жалғыздығының белгілерінің бірі – сығылған бейнелер принципі болып табылады.

- толық метрикалық кеңістік, ал А операторы кеңістігінің элементтерін сол кеңістіктің өзіне бейнелейтін оператор болсын. Егер кез-келген үшін

(1)

теңсіздікті қанағаттандыратын саны табылса, онда А операторын сығу операторы дейміз.

Кез-келген сығу операторы үздіксіз оператор болады. Шынында, егер болса, онда (1) теңсіздіктен . Егер нүктесі теңдеуінің шешуі болса, онда оны А операторының қозғалмайтын нүктесі дейді. Келешекте сығылған бейнелер принципін көп қолданатын болатын, төмендегі Банах теоремасына тоқтап кетелік.

Теорема (сығылған бейнелер принципі). - толық метрикалық кеңістігінде анықталған кез-келген сығу операторының жалғыз тек қана жалғыз қозғалмайтын нүктесі бар болады.

Дәлелдеу. кеңістігінен еркінше алынған нүктені деп белгілейік және болсын. Енді

(2)

тізбектің фундаментальдық тізбек екенін көрсетейік. Ол үшін, деп алып,

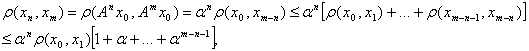
немесе

екенін көруге болады. Соңғы теңсіздікте болғандықтан жеткілікті үлкен үшін теңсіздіктің оң жағын керегімізше аз етіп алуға болады. кеңістігінің толықтығынан және (2) тізбек фундаментальдық тізбек болғандықтан, осы тізбектің шегі бар болады: . Ал операторының үздіксіздігінен

.

екендігі шығады. Сонымен, қозғалмайтын нүктенің бар екендігі дәлелденді. Енді

(3)

болса, онда

(4)

теңдігі орындалады. Соңғы формуладан (1) теңсіздік бойынша мына

(5)

теңсіздікке келеміз. Ал болғандықтан (5) теңсіздіктен , яғни болғандықтан (4.13) теңсіздіктен 3)

(4.9) теңсіздік бойынша мына

к болғандықтан, осы тізбектің шегі бар болады: сығылған і өзі.

Ескерту. Бүкіл кеңістігінде емес, тек нүктесінің белгілі бір тұйық аймағында ғана (1) теңсіздік орындалатын А операторы жиі кездеседі. Бұл нүктенің аймағы ретінде центрі нүктесінде жататын, радиусы болатын тұйық шарды қарастыруға болады. Осы шарды деп белгілейік. Егер А операторы Т шарын өзіне өзін бейнелейтін болса, онда сығылған бейнелер принципінің орынды болатынын дәлелдеуге болады.

Математикалық физиканың біраз шеттік есептерін зерттеу осы есептерге эквивалентті интеграл теңдеулерді қарастыруға әкеледі. Сондықтан, интеграл теңдеулер ұғымына қысқаша тоқтап өтейік. Мынадай

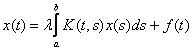(5)

теңдеуді қарайық.

Егер (5) теңдеудегі және функциялары сәйкес түрде сегменті мен квадратында үздіксіз функциялар болса, ал функциясы сегментінде белгісіз болса, онда бұл (5) теңдеу Фредгольмнің екінші текті интегралдық теңдеуі деп аталады. Егер (5) теңдеудің сол жағындағы функциясы нөлге тең болса, онда (5) теңдеуі Фредгольмнің бірінші текті сызықтық интегралдық теңдеуі дейміз.

Енді сығылған бейнелер принципінің көмегімен Фредгольмнің екінші текті сызықтық интегралдық теңдеудің кеңістігінде жалғыз шешуі бар болатынын көрсетейік. Ол үшін (5) теңдеудің оң жағымен анықталатын операторды А деп белгілейік:

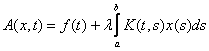(6)

Үздіксіз функциялардың кеңістігінен кез-келген және функцияларын қарайық. Онда (4.15) формула бойынша

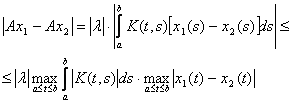(7)

жаза аламыз. Енді кеңістігінің нормасын пайдаланып, теңсіздіктен мынадай

(8)

теңсіздікке келеміз, мұнда

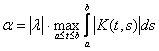(9)

Егер интегралдың төменгі шегі шекті сан болса және үшін ядросы нөлге айналса, онда Фредгольмнің екінші текті сызықтық теңдеуін Вольтерраның екінші текті сызықтық интегралдық теңдеуі деп атаймыз. Вольтерраның екінші текті сызықтық интегралдық теңдеуін мынадай

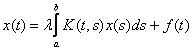(10)

түрде жазамыз. Ал егер (10) теңдеудің сол жағындағы функциясы нөлге тең болса, онда (10) теңдеуді Вольтерраның бірінші текті сызықтық интегралдық теңдеуі деп атайды.

Фредгольмнің екінші текті сызықтық интегралдық теңдеулері үшін айтылғандай етіп сығылған бейнелер принципін пайдалансақ, онда кеңістігінде Вольтерраның екінші текті сызықтық интегралдық теңдеуінің шешуінің жалғыз болатынын көрсетуге болады.

Жалпы айтқанда, сығылған бейнелер принципінің көмегімен Фредгольмнің (Вольтерраның) сызықтық емес интегралдық теңдеуінің және Вольтерра типті екінші текті сызықтық емес интегралдық теңдеуі шешуінің бар болатындығын және оның жалғыз екенін көрсетуге болады. Вольтерраның бірінші текті сызықтық (сызықтық емес) теңдеулері туралы және бірінші текті операторлық теңдеулер туралы жоғарыдағыдай тұжырым жасауға болмайды.

Пайдаланылған әдебиеттер

1. Бахвалов Н.С. "Численные методы". – М.:Наука, 1975.-632с

2. Владимиров В.С. "Обобщенные функции в математической физике". – М.:Наука, 1976.-280с

3. Владимиров В.С. "Уравнения математической физики". – М.:Наука, 1988.-512с