Б.К.Утеджанова

«Нархоз» университеті, Алматы

Математика пәнінде дифференциалдық теңдеудің жалпы шешімін табу әдістері («Бағалау» мамандығы бойынша)

а) Дифференциалдық теңдеуінің жалпы шешімін табыңыз

Шешуі:Бұл екінші ретті оң жағы бар дифференциалдық теңдеу. Мұндай теңдеудің шешімі біртекті дифференциалдық теңдеудің шешімімен, теңдеудің дербес шешімінің қосындысы түрінде болады, яғни мұндағы біртекті дифференциалдық теңдеу шешімі, ал дифференциалдық теңдеудің дербес шешімі, енді осыларды жеке-жеке анықтаймыз. Алдымен біртекті дифференциалдық теңдеуінің шешімін табамыз, ол үшін оның характеристикалық теңдеуін құрып, теңдеуді шешеміз. Характеристикалық теңдеу түрінде жазылады, бұл квадрат теңдеу, оның түбірлері: , яғни комплекс сан, (түбір табу мектеп бағдарламасында) демек бұл дифференциалдық теңдеудің жалпы шешімі түрінде жазылады. Енді дербес шешімді түрінде іздеп, алдымен оның туындыларынтабамыз, ол:

, бұл функциясы, функциясының дербес шешімі болғандықтан оны туындыларымен бірге алғашқы теңдеудегі сәйкес орындарына қоямыз, яғни:

енді теңдіктің екі жағындағы айнымалы аргумент алдындағы коффициенттерін өз ара теңестіріп, белгісіз тұрақты шамаларының мәндерін анықтаймыз.

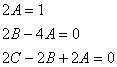немесе 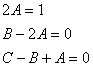бұдан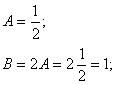

; демек

Сонымен берілген дифференциалды теңдеудің жалпы шешімі:

б) Коши есебінің шешімін табу керек

бастапқы шарты:

Шешуі: Теңдеудің екі жағында - қа бөліп, бірінші дәрежелі сызықты дифференциалды теңдеу аламыз:

Бұл теңдеудің шешімін түрінде іздейміз, сонда мұндағы функциялар, енді бұларды теңдеуге қойсақ

немесе () болады. Бұл теңдеуді шешу үшін, алдымен деп алып, функциясын анықтаймыз соңғы теңдеудің екі жағын жеке-жеке интегралдасақ, қандайда бір дербес шешім табылады

немесе бұдан (тұрақты шама )

Енді табылған шешімді екенін ескере отырып () теңдеуіне қойсақ, ол теңдеу төмендегідей түрге енеді:

теңдеудің екі екі жағында қысқартсақ болады, демек

; бұл теңдеудің екі жағын жеке-жеке интегралдасақ, екенін көреміз, яғни дифференциалдық теңдеудің жалпы шешімі , енді беріген бастапқы шартты пайдаланып, нің мәнін анықтаймыз. Ол үшін , тің орнына бастапқы шартта берілген мәндерін қойып теңдікті шешеміз:

Сонымен берілген дифференциалдық теңдеудің шешімі:

Әдебиет:

1) Қабдықайыров Қ. Жоғары математика Алматы.: Республикалық баспа кабинеті, 1993. 505 б.

2) Байбазаров М.Б., Ершбаев Ө.Д. Дифференциалдық және интегралдық есептеулер Алматы.: Білім, 1995. 176 б.