Горшков В.И., Святкина
А.А.
Пензенский
государственный университет архитектуры и
строительства,
Россия
Моделирование управляющих
моментов в газодинамическом регуляторе.
На первом этапе
исследований характеристик газодинамического регулятора экспериментальным путем
были получены зависимости крутящего момента на пластине [1]. Опытным путем было
выявлено, что крутящий момент на пластине зависит от двух факторов: угла
поворота пластины и скорости в её сечении.
Второй этап исследований
состоит из определения крутящего момента на крыльчатке газодинамического
регулятора. В виду сложности проведения эксперимента, связанного с большим
количеством влияющих на крутящий момент факторов, было принято решение о поиске
методов оптимального планирования эксперимента.
При планировании
эксперимента важно определить параметр, который необходимо оптимизировать. Процесс
оптимизации приводит в область факторного пространства, где кривизна
поверхности отклика велика и вследствие этого поверхность не может быть описана
многочленом вида [2]:
, (1)
где 
- свободный член; 
- линейные эффекты; 
- эффекты парного
взаимодействия.
Для адекватного
математического описания здесь требуется многочлен более высокой степени, а
именно отрезок ряда Тейлора [3]:
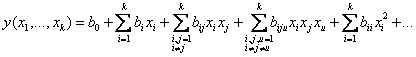, (2)
где - свободный член; 
- линейные эффекты; 
- эффекты парного
взаимодействия; 
- квадратичные
эффекты; 
- эффекты тройного
взаимодействия.
С этой целью было использовано ротатабельное центральное композиционное планирование. Этот
метод позволяет получать более точное математическое описание поверхности
отклика, что достигается благодаря увеличению числа опытов в центре плана и
специальному выбору величины звездного плеча α.
Ротатабельное центральное композиционное
планирование рассмотрено для двух факторов: скорость в сечении крыльчатки – Х1 (υ, м/с), площадь крыльчатки –Х2 (Sкр, см2). Функцией отклика у является крутящий момент на крыльчатке
Мкр,
мН·м. Матрица планирования и результаты эксперимента приведены в табл.
1.
Таблица 1
Матрица планирования и результаты эксперимента
|
Система опытов |
Номер опыта |
|
|
|
|
|
|
|
|
Полный факторный эксперимент |
1 |
-1 |
-1 |
+1 |
+1 |
+1 |
3 |
3,084 |
|
2 |
+1 |
-1 |
-1 |
+1 |
+1 |
3,7 |
3,784 |
|
|
3 |
-1 |
+1 |
-1 |
+1 |
+1 |
4 |
4,084 |
|
|
4 |
+1 |
+1 |
+1 |
+1 |
+1 |
4,8 |
4,884 |
|
|
Опыты в «звездных» точках |
5 |
+1,41 |
0 |
0 |
2 |
0 |
3,9 |
3,984 |
|
6 |
-1,41 |
0 |
0 |
2 |
0 |
3,1 |
3,184 |
|
|
7 |
0 |
+1,41 |
0 |
0 |
2 |
4,3 |
4,384 |
|
|
8 |
0 |
-1,41 |
0 |
0 |
2 |
3,4 |
3,484 |
|
|
Опыты в центре плана |
9 |
0 |
0 |
0 |
0 |
0 |
4 |
4,084 |
|
10 |
0 |
0 |
0 |
0 |
0 |
4,03 |
4,114 |
|
|
11 |
0 |
0 |
0 |
0 |
0 |
4,13 |
4,214 |
|
|
12 |
0 |
0 |
0 |
0 |
0 |
4,16 |
4,244 |
|
|
13 |
0 |
0 |
0 |
0 |
0 |
4,08 |
4,164 |
Для нахождения коэффициентов
регрессии вычисляем следующие вспомогательные коэффициенты:
, (3)
где n
– число факторов;
N – общее число опытов ротатабельного
центрального компазиционного планирования;
N0 – число опытов в центре плана.
. (4)
.
(5)
На основании результатов опытов
получаем вспомогательные суммы:
(6)
(7)
(8)
(9)
(10)
(11)
Рассчитываем коэффициенты регрессии:
(12)
(13)
(14)
(15)
(16)
(17)
На основании результатов опытов,
проведенных в центре плана, находим оценку дисперсии воспроизводимости:
.
(18)
Тогда 
при числе степеней
свободы f=N0-1=4.
Вычисляем оценки дисперсий в
определении коэффициентов регрессии:
(19)
(20)
(21)
(22)
По приложению 3 [4] находим t=2,78 для f=4 и Р=0,95. Тогда
Проверяем значимость коэффициентов
регрессии:
>
коэффициент значим;
>
коэффициент значим;
>коэффициент значим;
<
коэффициент незначим;
>
коэффициент значим;
>коэффициент значим.
Вычисляем оценку дисперсии
адекватности:
.
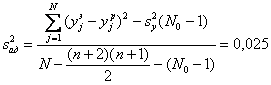(23)
Определяем число степеней свободы,
связанных с этой оценкой дисперсии:
. (24)
Расчетное значение критерия Фишера:
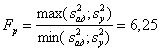<F (приложение
4[4]). Следовательно, уравнение регрессии адекватно описывает поверхность
отклика:
.
(25)
В уравнении регрессии
(25) перейдем от кодированных переменных Х
к физическим. Для этого запишем координаты центра плана х01=8 см2, х02=3,06 м/с и шаги варьирования Δх1=1,2 см2, Δх2=0,317 м/с. Тогда
справедливы следующие выражения [4]:
;
(26)
. (27)
Подставляя полученные
выражения (26), (27) в уравнение (25) получим:
(28)
Пользуясь полученным уравнением,
построим график зависимости крутящего момента Мкр от площади
крыльчатки Sкр и скорости в сечении крыльчатки υ (рис. 1).
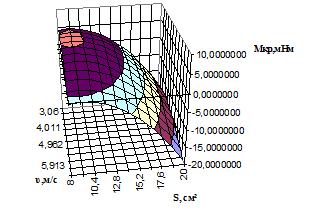
Рисунок 1 – Зависимость Мкр=f(Sкр, υ).
Таким образом, полученная поверхность
отклика на рисунке 1 позволяет производить анализ изменения крутящего момента на
крыльчатке в зависимости от её площади и скорости в сечении крыльчатки.
Список использованных источников.
1. Горшков В.И., Святкина А.А., Мирошниченко Д.С., Тараканов О.В. Выбор
параметров газодинамического регулятора расхода воздуха в системе
вентиляции//Региональная архитектура и строительство. – 2014. - №1(18). – С.
156-161.
2. Адлер Ю.П., Маркова
Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий.
– М.: Изд. «Наука», 1976.
3. Гайданин
А.Н., Ефремова С.А. Использование метода композиционного планирования
эксперимента для описания технологических процессов: метод. указания/ВолгГТУ. – Волгоград, 2008. – 16с.
4. Саутин
С.Н. Планирование эксперимента в химии и химической технологии. – Л.: «Химия»,
1975.