Педагогические науки/2. Проблемы подготовки специалистов

К.п.н. Титова Е.И.

Пензенский государственный университет архитектуры и строительства, Россия

Требования к профессионально-ориентированным математическим задачам строительства

Приложения математики весьма разнообразны. И при ее изучении в строительном вузе необходимо решать именно прикладные задачи строительства. Задачи в обучении математике, как известно, играют роль многоаспектного явления. Они могут выступать в качестве: носителя действий, адекватных содержанию математики; средства целенаправленного формирования знаний, умений, навыков; способа организации и управления учебно-познавательной деятельностью студентов; одной из форм реализации методов обучения; средства связи теории с практикой. В частности, применение в обучении математике у студентов строительных специальностей профессионально ориентированных задач позволяет формировать у будущего специалиста необходимые профессиональные качества.

Переходя к понятию профессионально ориентированной задачи в строительстве, заметим, что в качестве задачной ситуации в ней выступает некая модель профессиональной ситуации, в которой по известным характеристикам профессионального объекта или явления надо найти другие его характеристики или свойства. Разрешение или исследование представленной профессиональной ситуации способствует развитию у субъекта определенных профессиональных качеств.

Приведем примеры профессионально ориентированных задач, используемых при изучении математики.

1. При разработке гипсового композита исследовалось влияние на плотность , в сухом состоянии введения вспученного перлитового песка в количестве от 0 до от массы гипса при формировании изделий из технологической смеси нормальной густоты (по Суттарду). При гипотезе линейного снижения в зависимости от нормализованного фактора нужно найти две оценки МНК в модели по результатам пяти опытов, представленных в таблице.

p	-1	-0,5	0	0,5	1
xi	1228	1136	1120	4144	9142

2. Балка (с модулем упругости Е и моментом инерции J) наглухо заделана в конце О и подвергается действию сосредоточенной вертикальной силы Р, приложенной к концу балки L на расстоянии от места закрепления. Определить прогиб балки h на конце балки L.

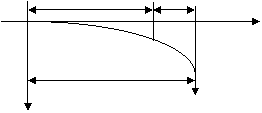x l-x

N x

y l Р

3. Интенсивность тепловыделения бетона пропорциональна не выделившемуся к данному моменту времени количеству тепла: , где - максимальное количество тепла, которое может выделиться в бетоне данного состава при полной гидратации цемента, - параметр, зависящий от типа цемента (для бетонов на портландцементе он изменяется в пределах от 0,010-0,015 1/ч). Определить функцию интенсивности тепловыделения бетона.

Таким образом, профессионально ориентированная математическая задача – это задача, условие и требование которой определяют собой модель некоторой ситуации, возникающей в профессиональной деятельности инженера-строителя, а исследование этой ситуации средствами математики способствует профессиональному развитию личности студента.

Вышесказанное позволяет нам сформулировать требования, предъявляемые к профессионально ориентированным задачам, используемым в рамках математической подготовки будущего строителя:

1) задача должна описывать ситуацию, возникающую в профессиональной деятельности инженера - строителя;

2) в задаче должны быть неизвестны характеристики некоторого профессионального объекта или явления, которые надо исследовать субъекту по имеющимся известным характеристикам с помощью средств математики;

3) решение задач должно способствовать прочному усвоению математических знаний, приемов и методов, являющихся основой профессиональной деятельности инженера – строителя;

4) задачи должны обеспечить усвоение взаимосвязи математики с общетехническими и специальными дисциплинами;

5) содержание задачи и ее решение требуют знаний по специальным предметам;

6) содержание профессионально ориентированной математической задачи определяет пропедевтический этап изучения понятий специальных дисциплин;

7) решение задач должно обеспечивать математическое и профессиональное развитие личности инженера - строителя.

Литература

1. Крымская Ю.А., Титова Е.И., Ячинова С.Н. Построение математических моделей в прикладных задачах// Молодой ученый. 2013. № 12 (59). С. 3-6.

2. Крымская Ю.А., Титова Е.И., Ячинова С.Н. Профессиональная подготовка строителей через решение математических задач// Современные проблемы науки и образования. 2014. № 2. С. 168.

3. Куимова Е.И., Куимова К.А., Титова Е.И. Прикладная направленность курса математики в строительном вузе// Молодой ученый. 2014. № 11. С. 390-391.

4. Титова Е.И., Чапрасова А.В. Категории профессионально ориентированных математических задач // Международный журнал прикладных и фундаментальных исследований. – 2015. – № 4 (часть 2) – С. 210-212.