К.е.н., Корецький С.Л.

Київський національний університет технології та дизайну

К.е.н., Молдованок М.И.

Київський інститут міжнародної економіки та підприємництва

Галата М.Л.

АТ Полісся, експерт

Нелінійні математичні моделі для визначення стратегії розвитку комерційної діяльності в умовах ринкової економіки

В економічній науці вже багато років з успіхом використовуються різні математичні моделі і відповідні методи розв’язання виникаючих при цьому задач. Серед них такі відомі, як модель міжгалузеву балансу (модель Лєонт¢єва), транспортна задача, моделі розподілу ресурсів і т.п. Ці всі моделі є лінійними, оскільки зв’язки між змінними визначаються лінійними функціями і лінійними обмеженнями. Внаслідок цього вони мають певну область застосування, і, незважаючи на їх безсумнівну користь, потребують вдосконалення. Тому останніми роками все ширше в теоретичну економіку вводяться нові нелінійні моделі, коли економічна наука будується за зразком точних та природничих наук.

Як з’ясувалося, класична (ортодоксальна) економіка не в змозі ні передбачити, ні пояснити розвиток реальної економіки за останні десятиріччя. Крім того, в природничих науках накопичено багатий досвід побудови і дослідження динамічних моделей систем, що розвиваються. Внаслідок цього і з’явились альтернативні напрямки. Їх об’єднує загальна ідея про те, що економіка не повинна відокремлюватись від інших природничих наук, а, навпаки, повинна розвиватися разом і використовувати їх досягнення. В першу чергу мова іде о теорії систем, що розвиваються, так звана, синергетика, яка широко застосовується в фізиці, хімії і, особливо, в біології. В тому ж ключі набувала розвитку і еволюційна економіка.

В математичних моделях ортодоксальної економіки це формулюється у вигляді цільових функцій та додаткових умов. При цьому, ринкова рівновага досягається за фіксованих значеннях параметрів, тому такі моделі є статичними. Неврівноважені процеси розглядаються тільки поблизу точок рівноваги, коли результат процесу вже певним чином визначено.

В математичних моделях еволюційної економіки це формалізується у вигляді функцій попиту, пропозицій, доходів і витрат. При цьому ринкова рівновага досягається за фіксованих значеннях параметрів, тому такі моделі є статичними. Неврівноважені процеси розглядаються тільки поблизу точок рівноваги, коли результат процесу вже певним чином визначено.

Вважається, що розвиток проходить нерівномірно, і періоди плавної еволюції чергуються з кризами. Протягом плавних періодів проходить вдосконалення, а в критичних ситуаціях реалізується перехід до іншого стаціонарного стану. Зауважимо, що як ортодоксальна, так і еволюційна економіка, побудовані на ринкових відношеннях, і тому обидві вони відносяться до ринкових економік. Головна відміна полягає в тому, що еволюційна економіка передбачає розгляд динаміки процесу і використовує нелінійні моделі.

Поставимо задачу: до якої границі можливо нарощувати кількість надаваних послуг за різних умов, які складаються на ринку. Зауважимо, що всі процеси відбуваються у часі, тому зручно розглядати не саму кількість послуг , а швидкість зміни їх кількості у часі . В цьому випадку приходимо до звичайних диференційних рівнянь, або до їх дискретного аналогу.

Якщо проміжок часу, що розглядається не досить великий, то будемо мати автономне диференційне рівняння

. (2)

де - деяка неперервна функція, яка визначається із статистичних даних.

Розглянемо випадок, коли стратегія вибору розвитку починається з нуля, тобто швидкість приросту прибутку в початковий момент дорівнює нулю. Тоді розвинувши функцію в ряд Тейлора в околі початкового значення і зберігши тільки лінійний член, отримаємо рівняння вигляду

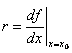, (3)

Рівняння (3) відображує відому мальтузіанську модель експоненціального зростання і має розв’язок

(4)

де, - початкове значення виробленої продукції, - показник зростання.

Якщо , то прибуток буде необмежено зростати, а якщо , то спадати, прямуючи до нуля. Нас цікавить зростання прибутку, а це означає, що приріст кількості надаваних послуг в одиницю часу при сталій ціні повинен неперервно зростати, що може реалізуватися лише за умов розширеного виробництва.

Далі розглянемо випадок, коли . Це означає, що перше наближення не дає відповіді на можливе зростання, оскільки , і потрібно використовувати наступний член розкладу в ряд Тейлора. Покладемо . Тоді розв’язок рівняння (2) за тих же початкових умов, що і вище, має вигляд

. (5).

Рівняння (5) задає так званий закон “гіперболічного зростання”. Для фактичного зростання потрібно, щоб було , а саме зростання може відбуватися лише для тих значень часу, коли .

Зрозуміло, що такі прості моделі мають обмежене застосування, оскільки вони дають нескінчене зростання кількості послуг у часі, але їх можливо використовувати, зокрема, в умовах досить великого попиту, відсутності конкуренції, але тільки на малих проміжках часу.

Більш реалістичними є моделі, які враховують обмеженість попиту, наприклад, так звана “модель логістичного зростання”. В рамках цієї моделі права частина рівняння (2) приймається у вигляді опуклої вгору функції з екстремумом, наприклад у вигляді поліному другого ступеня. В цьому випадку на відміну від (2), матимемо диференційне рівняння вигляду

. (6)

де - деякі константи. В порівнянні з рівнянням (2) маємо додатковий член в правій частині. Параметр має зміст граничної кількості вироблених послуг, коли ще існує попит на них. Це нелінійне рівняння має дві важливі властивості. Так, при малих кількість послуг зростає, а при великих - прямує до деякої межі . Отже рівняння описує обмежене зростання кількості послуг.

Розв’язок рівняння (6) із врахуванням початкових умов має вигляд

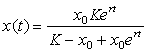. (7)

З формули (7) випливає, що поведінка розв’язку залежить від початкових умов. Якщо початкова кількість , то функція спадає, а в протилежному випадку – зростає, і, якщо , функція має точку перегину з координатами .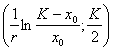

Модель логістичного зростання зручно застосовувати при виході на ринок з новим типом послуг. З неї випливає дуже простий рецепт: для більш швидкого нарощування прибутку початкова кількість нових послуг не повинна бути досить великою, і ні в якому разі не повинна перевищувати певної межі. Ця умова узгоджується із здоровим глуздом, оскільки суттєво зменшує ризик втрати вкладених коштів при початку реалізації нового типу послуг.

Нами також реалізовані дискретні моделі розвитку, які спираються на дані офіціальних джерел, які наводять статистичні дані тільки з певним періодом. Ці моделі були застосовані для розробки стратегії розвитку надання рекламних послуг, а також для прогнозування зміни цін на вторинному ринку житла у місті Києві. Отримані в роботі результати добре узгоджуються з даними спостережень.

Литература:

1. Чернавский Д.С., Старков Н.И., Щербаков А.В. О проблемах физической экономики // Успехи физических наук. . 2002. . Т. 172, ? 9. . С. 1045-1066.
2. Резниченко Г.Ю. Лекции по математическим моделям в биологии. - М.-Ижевск, 2002. . Часть 1. . 231с.