Гладкая кривая и ее
определение в широком смысле
Айдос Е.Ж.
Казахский технический университет имени К.И.Сатпаева, г.Алматы,
Казахстан,
e-mail:
erkaraai@mail.ru
В статье раскрывается
теоретическая
проблема известного
определения гладкой кривой; вводится понятие «угловой функции» и с его помощью формулируется новое определение
для широкого
класса гладких кривых, в котором снято противоречие,
присущее известному определению понятия гладкой кривой.
Приведем вышеназванное известное определение
гладкой кривой.
П-определение (см.
напр., [1], §5.15 ). Функция f называется
гладкой на отрезке ![]() , если она
имеет непрерывную производную на этом
отрезке.
, если она
имеет непрерывную производную на этом
отрезке.
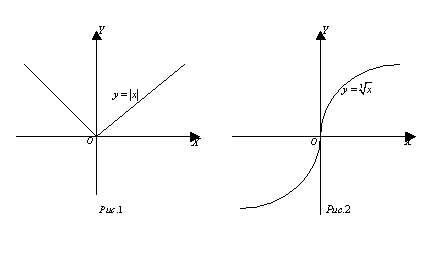
Вместе с тем, как показывает пример
негладких в смысле приведенного определения функций ![]() и
и ![]() (см.Рис.1 и 2) с
интуитивной точки зрения
первая «негладкая» по причине наличия «угловой точки» графика функции
(см.Рис.1 и 2) с
интуитивной точки зрения
первая «негладкая» по причине наличия «угловой точки» графика функции ![]() в то время как
график функции
в то время как
график функции ![]() геометрически никак
не относится к «негладкой». Конечно, здесь причина в том, что производная
геометрически никак
не относится к «негладкой». Конечно, здесь причина в том, что производная ![]() в точке
в точке ![]() не является
непрерывной, и потому непопадает под П-определение. Можно рассуждать и так:
функция
не является
непрерывной, и потому непопадает под П-определение. Можно рассуждать и так:
функция ![]() очевидным образом
«гладкая», так что геометрически и обратная к ней функция
очевидным образом
«гладкая», так что геометрически и обратная к ней функция ![]() так же должна
относиться к классу «гладких».
так же должна
относиться к классу «гладких».

Введем понятие «угловой функции». Сначала дополняя с некоторыми для нас
важными вопросами, приведем определение понятия «касательной» к
кривой, данного в ![]()
Пусть кривая Г задана уравнением y=f(x),![]() и
и ![]() некоторая ее
точка. Возьмем точку
некоторая ее
точка. Возьмем точку ![]() и проведем прямую S
через точки
и проведем прямую S
через точки ![]() и
и ![]() (на
Рис.3:
(на
Рис.3: ![]() на Рис.4:
на Рис.4: ![]() ). Выберем направление прямой S
так, чтобы угол b
между положительным направлением оси Оx и направлением прямой S
был бы острым:
). Выберем направление прямой S
так, чтобы угол b
между положительным направлением оси Оx и направлением прямой S
был бы острым: ![]() Полученную
таким образом, направленную прямую S назовем секущей, а b - углом наклона секущей. Чтобы показать, что секущая проходит через точек с абсциссами
Полученную
таким образом, направленную прямую S назовем секущей, а b - углом наклона секущей. Чтобы показать, что секущая проходит через точек с абсциссами ![]() и
и ![]() будем писать ее угол наклона в виде:
будем писать ее угол наклона в виде: ![]()
Если при ![]() угол
наклона
угол
наклона ![]() секущей
стремится к конечному числу a,
то секущая S стремится к направленной
прямой Т, у которой угол наклона
равен a. Поскольку полученная прямая Т проходит через точку с абсциссой
секущей
стремится к конечному числу a,
то секущая S стремится к направленной
прямой Т, у которой угол наклона
равен a. Поскольку полученная прямая Т проходит через точку с абсциссой ![]() ее угол наклона
обозначим в виде
ее угол наклона
обозначим в виде ![]()
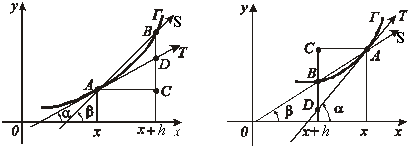

![]() Рис.3 Рис.4
Рис.3 Рис.4
Определение. Направленная прямая Т, проходящая
через точку![]() кривой Г:
кривой Г: ![]() называется касательной
к кривой в этой точке, если ее угол наклона равен пределу угла наклона секущей S, проходящей через точек
называется касательной
к кривой в этой точке, если ее угол наклона равен пределу угла наклона секущей S, проходящей через точек![]() и
и ![]() при
при ![]() т.е.
т.е. ![]()
Обратим
внимание на то, что значения угла наклона секущей: ![]() а значения угла наклона направленной прямой:
а значения угла наклона направленной прямой: ![]() .
.
Таким образом, если во всех точках
отрезка ![]() существует предел
существует предел ![]() то на этом
отрезке определена функция
то на этом
отрезке определена функция ![]() значения которой находятся на отрезке
значения которой находятся на отрезке![]() и потому назовем ее угловой функцией касательных.
и потому назовем ее угловой функцией касательных.
Из определения ясно
следует, что существование
касательной к графику Г функции y=f(x) в точке![]() равносильно
существованию угловой функции
равносильно
существованию угловой функции
![]()
![]() (1)
(1)
Например, в точке А кривой, изображенной на Рис.5 нет
касательной, ибо![]()
![]() (
(![]() т.е. угловая
функция в этой
точке
не определена. Но в точке А существуют
левосторонная и правосторонная касательные с углами наклона, равными соответственно
т.е. угловая
функция в этой
точке
не определена. Но в точке А существуют
левосторонная и правосторонная касательные с углами наклона, равными соответственно
![]() и
и ![]() (см.
также, пример 1).
(см.
также, пример 1).
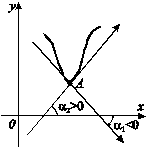
Рис.5
Так как угол наклона секущей равен ![]() (см. Рис.3 и 4), то учитывая непрерывность функции
(см. Рис.3 и 4), то учитывая непрерывность функции ![]() в любой точке, получим
в любой точке, получим
![]() (2)
(2)
Теперь приведем
определение гладкой кривой с помощью угловой функции.
К-Определение.
Кривая, заданная уравнением ![]()
![]() называется гладкой
на отрезке
называется гладкой
на отрезке![]() если определена и непрерывна угловая функция касательных на
если определена и непрерывна угловая функция касательных на ![]()
Приведенные здесь определения касательной и гладкой кривой, позволяют получать решения многих теоретических проблемных
вопросов математического анализа (см. ![]() ). В данной статье мы
продемонстрируем лишь решение вышеуказанной проблемы, вытекающей из П-определения
с помощью К-определения.
). В данной статье мы
продемонстрируем лишь решение вышеуказанной проблемы, вытекающей из П-определения
с помощью К-определения.
Сначала выпишем равенство (2) в виде: ![]() Отсюда следует, что если
существует и непрерывна производная
Отсюда следует, что если
существует и непрерывна производная ![]() функции, то существует
непрерывная угловая функция
функции, то существует
непрерывная угловая функция ![]() (как композиция двух
непрерывных функций). Поэтому, любая кривая, гладкая по П-определению
будет гладкой и по К-определению.
(как композиция двух
непрерывных функций). Поэтому, любая кривая, гладкая по П-определению
будет гладкой и по К-определению.
Но, обратное утверждение не верно. Например, функция ![]() - по
- по
К-определению, гладкая, но по П-определению
она не будет гладкой на отрезке ![]() .
Действительно, для нее существует угловая функция:
.
Действительно, для нее существует угловая функция: 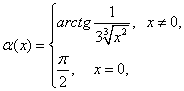 и она непрерывна на отрезке
и она непрерывна на отрезке ![]() Справедливость последнего утверждения достаточно
показать лишь в точке
Справедливость последнего утверждения достаточно
показать лишь в точке
![]() а для точек
а для точек ![]() непрерывность угловой
функции следует из известного свойства элементарных функций. Имеем,
непрерывность угловой
функции следует из известного свойства элементарных функций. Имеем, ![]() т.е. функция
т.е. функция ![]() непрерывна и в точке
непрерывна и в точке ![]() Следовательно, по К-определению, данная функция на
отрезке
Следовательно, по К-определению, данная функция на
отрезке ![]() - гладкая. А то что, она не гладкая по П-определению, следует
как отмечено выше, из разрывности производной функции:
- гладкая. А то что, она не гладкая по П-определению, следует
как отмечено выше, из разрывности производной функции: 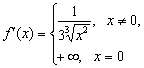 в точке
в точке ![]()
Пример1. На отрезке ![]() функция
функция ![]() -
не гладкая, так
как, в точке
-
не гладкая, так
как, в точке ![]()
для нее не определена угловая
функция. Действительно, (см.(1) и (2))
![]()
![]()
![]() В этой точке существуют лишь
односторонние касательные с углами наклона, соответственно
В этой точке существуют лишь
односторонние касательные с углами наклона, соответственно ![]() и
и ![]()
Пример 2. Функция 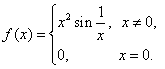 на отрезке
на отрезке ![]() - не гладкая, поскольку
- не гладкая, поскольку
для нее хотя определена
угловая функция, равная 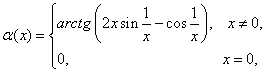 но
но
она не является непрерывной в
точке ![]() (функция
(функция ![]() в точке
в точке ![]() не имеет предела).
не имеет предела).
Мы видели, что диапозон применяемости К-определения достаточно широкий, у него отсутствует теоретические проблемы, подобные в П-определении. К-определение
является естественным
и полноценным для понятия гладкой кривой, и потому его можно
предложить для
широкого пользования в математике и в других отраслях наук, применяющих математику.
Основные причины наличия теоретической проблемы известного определения гладкой кривой, а также
другие проблемные вопросы
математического анализа и их решения
смотрите в ![]() и
и ![]()
- С.М.Никольский, Курс математического анализа, т.1, «Наука», 1983;
2.
Я.С.Бугров, С.М.Никольский, Дифференциальное и
интгральное исчисление, «Наука», 1980;
3.
Е.Ж.Айдос, Жоғары математика, 2-бөлім, «Бастау», 2008;
- Aydos E.Zh. About determination Mathematical Concept Through
characters![]() . // Of the third
Congress of the world Mathematical society of Turkic
. // Of the third
Congress of the world Mathematical society of Turkic
Countries, June 30 - July 4, 2009 // Третий конгресс Всемирного математического
общества тюркоязычных стран, 30 июня – 4 июля 2009 года.