Козлова Л.И.

Восточно-Казахстанский государственный технический университет

им. Д. Серикбаева, Казахстан

Обобщенная теорема синусов

В данной статье рассматривается произвольный треугольник и самые знаменитые связанные с ним точки и линии: центр описанной окружности, медианы, центроид, биссектрисы углов, центр вписанной окружности, центры вневписанных окружностей, высоты, ортоцентр, прямую Эйлера и окружность девяти точек.

Изучение биссектрис углов естественно подводит нас к теореме Штейнера – Лемуса, которая сотни лет считалась трудной для доказательства.

Наконец, по треугольнику и точке Р, находящейся в общем положении, мы получаем новый треугольник, вершины которого являются основаниями перпендикуляров из точки Р к сторонам данного треугольника. Эта идея приводит к занимательным результатам, которые будут рассмотрены в статье.

Теорема синусов – это тригонометрическая теорема, которой мы будем часто пользоваться. К сожалению, она обычно появляется в учебниках в урезанной форме, и в этом виде она не приносит всей той пользы, которую могла бы дать обобщенная теорема. Мы начинаем с треугольника АВС (обозначенного обычным способом) и описываем вокруг него окружность с центром в точке О и радиусом R, как показано на рисунках 1 и 2.

Проведем диаметр CJ и хорду ВJ. В обоих случаях ÐСВJ – прямой, так как он вписан в полукруг. Следовательно, на обоих рисунках

.

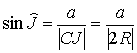На рисунке 1 =, поскольку углы J и А опираются на одну и ту же дугу окружности. На рисунке 2 = 180⁰ – , потому что противоположные углы вписанного четырехугольника являются дополнительными. Вспоминая, что sin q = (180° – q), получим, что в обоих случаях sin = sin , следовательно, sin = a/2R, т.е.

.

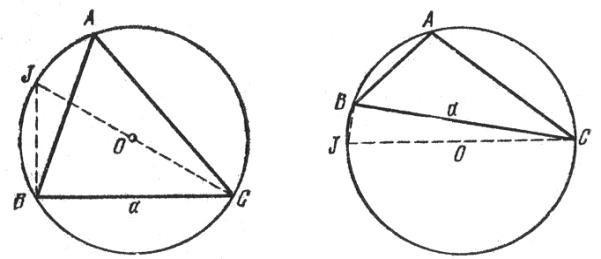
Рисунок 1 Рисунок 2

Та же самая процедура, примененная к другим углам треугольника АВС, дает

.

Объединяя результаты, мы можем сформулировать обобщенную теорему синусов следующим образом:

Теорема 1. Для треугольника АВС с радиусом описанного круга R выполнены соотношения:

.

Отрезок, соединяющий вершину треугольника с некоторой точкой на противоположной стороне, называется чевианой. Таким образом, если в треугольнике AВС Х, Y и Z – точки, лежащие на сторонах ВС, СА, АВ соответственно, то отрезки АХ, ВY, СZ являются чевианами.

Этот термин происходит от имени итальянского, математика Джованни Чевы, который в 1678 году опубликовал следующую очень полезную теорему:

Теорема 2. Если три чевианы АХ, ВY, СZ (по одной из каждой вершины) треугольника АВС конкуренты, то

.

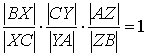Когда мы говорим, что три прямые (или отрезка) конкурентны, то мы имеем в виду, что все они проходят через одну точку, которую, обозначим через Р.

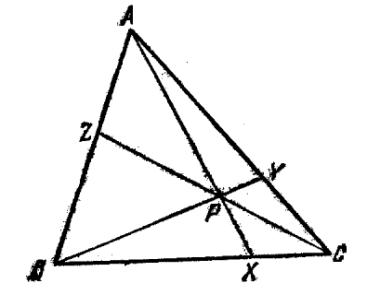
Рисунок 3

Для доказательства теоремы Чевы вспомним, что площади треугольников с равными высотами пропорциональны основаниям треугольников. Ссылаясь на рисунок 3, мы имеем:

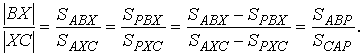
Аналогично,

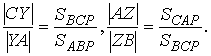
Теперь, если мы перемножим их, то получим

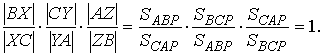
Теорема, обратная к этой теореме, также верна.