К. ф.-м. н. Марзан С.А., к. ф.-м. н. Мирская Е.Е

Брестский государственный университет имени А.С. Пушкина,

Республика Беларусь

Существование решения задачи Коши

для дифференциального уравнения с дробной производной Капуто в пространстве непрерывно-дифференцируемых функций

В связи с приложениями в теории интегральных и дифференциальных уравнений важной задачей является исследование краевых задач для нелинейных дифференциальных уравнений с дробными производными.

Настоящая работа посвящена исследованию вопроса существования решения задачи Коши для нелинейного дифференциального уравнения с дробной производной Капуто [1] порядка  

               ,                (1)

где  при ,  при , в пространстве

.

Пусть функция  действует из  в R, при любом  :

                                      .                                           (2)

В работе [2] показано, что при выполнении условия (2) функция  является решением задачи Коши (1) тогда и только тогда, когда она является решением интегрального уравнения

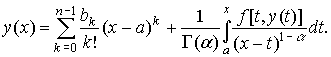                                                    (3)

Для установления разрешимости задачи Коши (1) в пространстве  к условию (2) добавим два дополнительных условия:

                                 (xÎ[a,b], yÎR),                                     (4)

где L>0, d>0 – некоторые постоянные, и

                                          AL<1, A=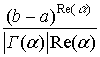.                                              (5)

Теорема 1. Пусть aÎC (Re(a)>1, aÏN), и n=[Re(a)]+1. Пусть функция f:[a,b]´R®R удовлетворяет условию (2) и выполнены условия (4) и (5). Тогда задача Коши (1) имеет по крайней мере одно решение y(x) в пространстве .

Для доказательства теоремы строится последовательность уравнений

                                  ,

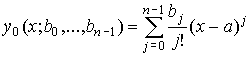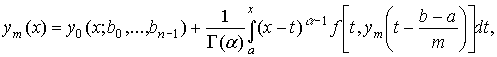                         (6)

                   при  .

Нетрудно видеть, что при каждом mÎN уравнение (6) имеет единственное решение ym(x)ÎC[a,b]. Это решение называется m-тым приближением Тонелли уравнения (3).

С использованием свойств дробных производных и интегралов Римана-Лиувилля показывается, что при сделанных предположениях последовательность приближений Тонелли ym(x) равномерно ограничена и равностепенно непрерывна в пространстве C[a,b]. Тогда (по теореме Арцела-Асколи [3, стр. 167]) для всех  последовательность ym(x) предкомпактна в C[a,b]. Поэтому из последовательности ym(x) можно выбрать подпоследовательность , сходящуюся к ÎC[a,b].

С использованием свойства непрерывности интегрального оператора

                               

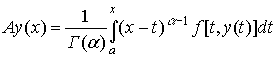
как оператора из пространства C[a,b] в пространство C[a,b] показывается, что функция  удовлетворяет уравнению (3).

Подставляя  в уравнение (3) и последовательно дифференцируя полученное тождество  (n=[Re(a)]+1) раз, заключаем, что  является решением задачи Коши (1) в пространстве Cn-1[a,b]. Из  следует, что Î, что и доказывает теорему.

Обозначим через   дробную производную Капуто функции  комплексного порядка:

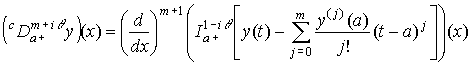      .                 (7)

Рассмотрим задачу Коши

                ,  ().                    (8)

Следствие. Пусть a=m+iq (mÎN, m>1, q¹0),  – дробная производная Капуто (7). Пусть функция f:[a,b]´R®R удовлетворяет условиям теоремы 1. Тогда задача Коши (8) имеет по крайней мере одно решение в пространстве .

Литература:

1. Caputo M. Linear model of dissipation whose Q is almost frequency independent // Geophis. J. Astronom. Soc. – 1967. –Vol. 13. – P. 529-539.

2. Килбас А.А. Нелинейные дифференциальные уравнения с дробной производной Капуто в пространстве непрерывно-дифференцируемых функций / А.А. Килбас, С.А. Марзан // Доклады академии наук. – 2004. – Т. 399, № 1. – С. 7-11.

3. Антоневич А.Б. Функциональный анализ и интегральные уравнения / А.Б. Антоневич, Я.В. Радыно. – Минск: БГУ, 2003. – 430 с.