К. т. н. Сметанкин В.А., к. т. н. Сметанкина Н.В., Сметанкин А.В.

Харьковский национальный технический университет сельского хозяйства имени Петра Василенко, Украина

Математическое моделирование акустических полей гидродинамических излучателей в замкнутых областях

Ультразвуковые колебания представляют собой упругие волны, распространяющиеся с определенной скоростью в какой-либо материальной среде – газах, жидкостях, твердых телах. Ультразвуковые колебания малой интенсивности, используемые для дефектоскопии и исследования вещества, подчиняются законам линейной акустики. Распространение высокоэнергетических колебаний в жидких и твердых средах сопровождается рядом новых эффектов, часто приводящих к необратимым явлениям. Эти эффекты, такие как радиационное давление, акустическая кавитация и звуковые потоки, изучаются в нелинейной акустике.

Ультразвуковая техника широко применяется во многих технологических процессах, например, при очистке различных поверхностей [1]. Разработано и выпускается большое количество ультразвукового оборудования для очистки деталей и полуфабрикатов, в частности гидродинамические излучающие системы [2, 3].

В настоящей работе рассматривается возможности ультразвуковой очистки в акустическом поле, формируемом системой гидродинамических излучателей (ГДИ). Основные элементы такого излучателя – конусно-цилиндрическое сопло, препятствие-отражатель и резонансная колебательная система в виде стержней, расположенных вдоль образующих цилиндра с осью – сопло-отражатель. Цилиндр рассматриваемого преобразователя имеет 16 стержней шириной 6 мм через 22,5 градуса. Длина цилиндра равна 126 мм, а его диаметр 37 мм. Излучатели устанавливаются в цилиндрическом резервуаре, наполненном жидкостью с поверхностно-активными веществами. Ее плотность равна 1010 кг/м³, скорость звука  м/с, кинематическая вязкость м²/с.

Как показывают теоретические и экспериментальные исследования [4], ГДИ при погружении их в жидкость на глубину 0,2–0,3 м могут рассматриваться как сферические источники нулевого порядка, а оценку эффективности их работы в замкнутых областях можно производить по величине звукового давления [5]. В этом случае выражения для звукового давления p и скорости движения среды v имеют вид

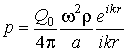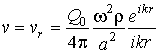, , (1)

где – производительность источника звука, – скорость звука; , w – круговая частота колебаний, , – цилиндрические координаты.

Скорость движения среды на больших расстояниях от точечного источника такова

.

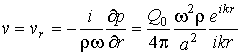Интенсивность звукового поля точечного источника вычисляется по формуле

.

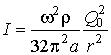Характеристики звукового поля определялись из нелинейных уравнений Эйлера в форме Навье-Стокса

, (2)

, , (3)

где – плотность жидкой среды.

Решение системы нелинейных дифференциальных уравнений осуществлялось итерационным методом. В качестве первой итерации предполагалось, что излучатель заменяется эквивалентной системой точечных источников (1), распределенных с интенсивностью w, зависящей от собственных частот и форм стержня излучателя. Решением однородных уравнений (2) является обобщенный потенциал простого слоя с плотностью w и ядром, определяемым компонентами матрицы Кельвина-Сомильяны

, .

По найденным значениям скоростей из уравнений (3) определяется плотность и давление жидкости. Следующий этап состоит в вычислении правой части уравнений (2), построении общего решения системы (2)-(3) и уточнении значений плотности и давления жидкости. Процесс завершается при достижении требуемой точности решения.

На основании изложенного получены расчетные характеристики ультразвукового поля, формируемом системой ГДИ в цилиндрическом резервуаре. Начало координат совпадает с геометрическим центром резервуара. Принималось, что в резервуаре по двум окружностям с радиусами м и м равномерно установлено 16 ГДИ (8 ГДИ на каждой окружности). ГДИ внутренней окружности расположены относительно ГДИ внешней окружности со смещением, равным 22,5 градусов. Все излучатели установлены на одинаковой высоте: , м, м.

На рис. 1 представлены результаты расчета звукового давления в различных сечениях по координате , т. е. по высоте резервуара при :  м (кривая 1),  м (кривая 2),  м (кривая 3),  м (кривая 4), м (кривая 5).

Во всех сечениях принимает максимальные значения при  м (радиус внутренней окружности установки ГДИ), а у стенок резервуара асимптотически приближается к 400 Па. Значения колебательной скорости среды v изменяются в диапазоне от 1,9×10^-3 м/с до 5,3×10^-2 м/с. При удалении от области расположения излучателей по высоте резервуара амплитудные значения параметров звукового поля также снижаются.

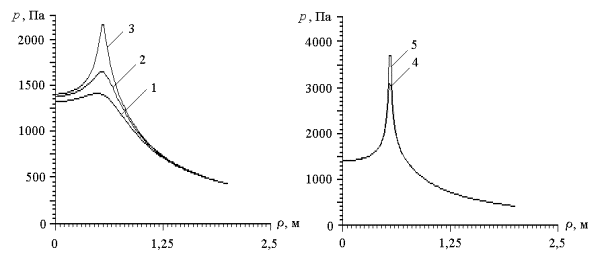
Рис. 1. Зависимость уровня звукового давления от расстояния

до источника для 16 ГДИ

С целью снижения энергоемкости и стоимости конструкции, но без потери качества производимой очистки, рассматривается возможное сокращение количества ГДИ. Для случая отключения ГДИ, расположенных на внешней окружности, на рис. 2 приведены зависимости звукового давления в разных сечениях цилиндра при , кривая 1 –  м, кривая 2 –  м, кривая 3 –  м, кривая 4 –  м, кривая 5 – м.

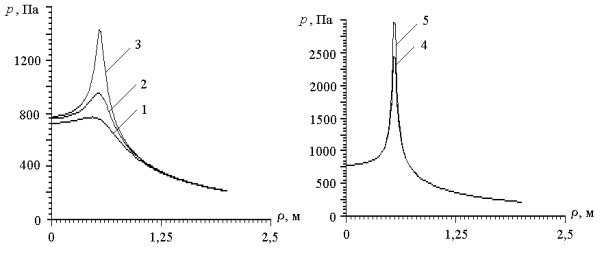
Рис. 3. Зависимость уровня звукового давления от расстояния

до источника для 8 ГДИ

Отключение ГДИ приводит к снижению звукового давления в 1,5 раза во всех сечениях по сравнению со случаем, когда включены обе системы ГДИ. Колебательная скорость снизилась незначительно.

Следовательно, отключение одной из систем ГДИ нецелесообразно, так как основным критерием оценки акустического поля, создаваемого гидродинамической излучающей системой, является уровень звукового давления в области, непосредственно примыкающей к излучателю, так как именно в этой области происходит интенсивная очистка.

Таким образом, установлено, что конструктивные параметры существенно влияют на эффективность работы гидродинамической излучающей системы.

Литература:

1. Применение ультразвука в промышленности / Под ред. А.И. Маркова.– М.: Машиностроение, 1975.– 240 с.

2. Марков А.И. Всесоюзная научно-техническая конференция "Новое ультразвуковое оборудование и аппаратура, опыт их применения" (Ультразвук-92) // Акуст. журнал.– 1992.– Т. 38, Вып. 2.– С. 380-381.

3. Шестаков В.П. Генерирование звука жидкоструйным свистком со сменными отражателями различной формы // Акустика и ультразвуковая техника.– 1996.– Вып. 21.– С. 18–21.

4. Назаренко А.Ф., Слиозберг Т.М., Каськов А.Н., Краковский И.А. Об одном способе генерирования колебаний гидродинамической излучающей системой // Акустика и ультразвуковая техника.– 1985.– Вып. 20.– С. 3–9.

5. Ультразвук. Маленькая энциклопедия.– М.: Советская энциклопедия, 1979.– 400 с.