Ленюк М. П.
Чернівецький факультет НТУ „ХПІ”
ГІБРИДНІ ІНТЕГРАЛЬНІ ПЕРЕТВОРЕННЯ ФУР’Є – БЕССЕЛЯ –ЕЙЛЕРА НА ДЕКАРТОВІЙ ОСІ
Запровадимо інтегральні перетворення, породжене на
множині
![]() гібридним
диференціальним оператором (ГДО).
гібридним
диференціальним оператором (ГДО).
![]() (1)
(1)
У рівності (1) ![]() - одинична функція
Гевісайда [1];
- одинична функція
Гевісайда [1]; ![]() - диференціальний
оператор Фур’є [2];
- диференціальний
оператор Фур’є [2]; ![]() - диференціальний
оператор Бесселя [3],
- диференціальний
оператор Бесселя [3], ![]() диференціальний оператор Ейлера [2];
диференціальний оператор Ейлера [2]; ![]() .
.
Означення. Областю визначення ГДО ![]() назвемо множину
назвемо множину ![]() вектор-функцій
вектор-функцій ![]() з такими властивостями: 1) існують такі числа
з такими властивостями: 1) існують такі числа ![]() та
та ![]() , що мають місце рівності
, що мають місце рівності
![]() (2)
(2)
2) функції ![]() задовiльняють умови спряження
задовiльняють умови спряження
![]() (3)
(3)
В
подальшому вважаємо, що виконані умови на коефіцієнти:
![]()
Оскільки
ГДО ![]() самоспряжений і має
дві особливі точки
самоспряжений і має
дві особливі точки ![]() та
та ![]() , то його спектр дійсний та неперервний [4]. Можна вважати,
що спектральний параметр
, то його спектр дійсний та неперервний [4]. Можна вважати,
що спектральний параметр ![]() . Йому відповідає комплекснозначна спектральна
вектор-функція:
. Йому відповідає комплекснозначна спектральна
вектор-функція:
![]() (4)
(4)
При цьому функції
![]() де
де ![]() , повинні задовольняти відповідно диференціальні рівняння
, повинні задовольняти відповідно диференціальні рівняння
![]()
![]()
![]() (5)
(5)
![]()
![]()
та умови спряження (3); ![]()
Фундаментальну
систему розв’язків для диференціального рівняння Фур’є ![]() складають функції
складають функції ![]() та
та ![]() [2]; фундаментальну систему розв’язків для диференціального
рівняння Бесселя
[2]; фундаментальну систему розв’язків для диференціального
рівняння Бесселя ![]() складають функції
складають функції ![]() та
та ![]() [3]; фундаментальну систему розв’язків для диференціального
рівняння Ейлера
[3]; фундаментальну систему розв’язків для диференціального
рівняння Ейлера ![]() складають функції
складають функції ![]() та
та ![]() [2].
[2].
Якщо,
маючи фундаментальну систему розв’язків, покласти
![]()
![]() (6)
(6)
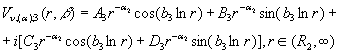
то умови спряження (3) дають вісім алгебраїчних
рівнянь для визначення 12-ти невідомих ![]() . Це явно недостатньо для побудови
спектральної вектор-функції методом спектральної задачі Штурма-Ліувілля.
. Це явно недостатньо для побудови
спектральної вектор-функції методом спектральної задачі Штурма-Ліувілля.
Скористаємось методом дельта-подібної
послідовності – ядро Коші як фундаментальна матриця розв’язків задачі Коші для
сепаратної системи диференціальних рівнянь теплопровідності параболічного типу,
породженої ГДО ![]() .
.
Побудуємо
обмежений в області ![]() розв’язок системи
диференціальних рівнянь теплопровідності параболічного типу [5]
розв’язок системи
диференціальних рівнянь теплопровідності параболічного типу [5]
![]()
![]() (7)
(7)
![]()
за початковими умовами
![]() (8)
(8)
та умовами спряження
![]() (9)
(9)
Припустимо,
що вектор-функція ![]() є оригіналом за Лапласом стосовно
є оригіналом за Лапласом стосовно ![]() [6]. В зображеннях за
Лапласом задачі (7) – (9) відповідає крайова задача: побудувати обмежений на
множині
[6]. В зображеннях за
Лапласом задачі (7) – (9) відповідає крайова задача: побудувати обмежений на
множині ![]() розв’язок сепаратної системи диференціальних рівнянь
Фур’є, Бесселя та Ейлера для модифікованих функцій
розв’язок сепаратної системи диференціальних рівнянь
Фур’є, Бесселя та Ейлера для модифікованих функцій
![]()
![]() (10)
(10)
![]()
за умовами спряження
![]() (11)
(11)
Фундаментальну
систему розв’язків для диференціального рівняння Фур’є ![]() утворюють функції
утворюють функції ![]() та
та ![]() [2]; фундаментальну систему розв’язків для диференціального
рівняння Бесселя
[2]; фундаментальну систему розв’язків для диференціального
рівняння Бесселя ![]() утворюють
модифіковані функції Бесселя
утворюють
модифіковані функції Бесселя ![]() та
та ![]() [3]; фундаментальну систему розв’язків для диференціального
рівняння Ейлера
[3]; фундаментальну систему розв’язків для диференціального
рівняння Ейлера ![]() утворюють функції
утворюють функції ![]() та
та ![]() [2];
[2]; ![]() - фіксуємо таку
вітку.
- фіксуємо таку
вітку.
Наявність
фундаментальної системи розв’язків дозволяє будувати розв’язок крайової задачі
(10), (11) методом функцій Коші [1,2]:
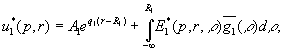
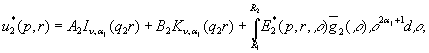 (12)
(12)
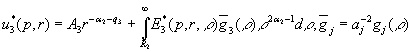 .
.
У рівностях (12) ![]() - функції Коші:
- функції Коші:
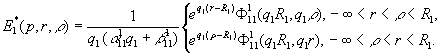 (13)
(13)
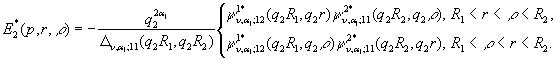 (14)
(14)
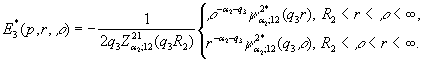 (15)
(15)
![]()
Умови спряження (11) для визначення величини ![]() та
та ![]() дають алгебраїчну
систему з чотирьох рівнянь:
дають алгебраїчну
систему з чотирьох рівнянь:
![]()
![]() (16)
(16)
У
системі (16) беруть участь функції
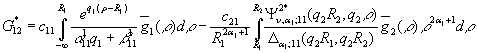
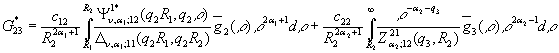 ,
,
та символ
Кронекера ![]() (
(![]() )
)
Введемо до розгляду функції:
![]()
![]()
![]()
![]()
Припустимо,
що виконана умова однозначної розв’язності даної параболічної задачі: для ![]() з
з ![]() , де
, де ![]() - абсциса збіжності
інтеграла Лапласа, та
- абсциса збіжності
інтеграла Лапласа, та ![]() визначник
алгебраїчної системи (16)
визначник
алгебраїчної системи (16)
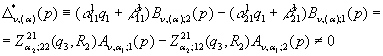 (17)
(17)
У
результаті однозначної розв’язності алгебраїчної системи (16) й підстановки
отриманих значень ![]() у рівності (12) маємо
єдиний розв’язок крайової задачі (10), (11):
у рівності (12) маємо
єдиний розв’язок крайової задачі (10), (11):
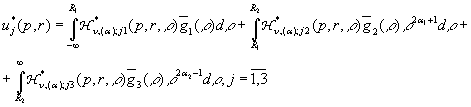 (18)
(18)
У рівностях (18) беруть участь
функції впливу:
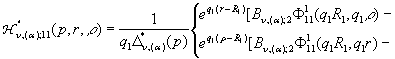
![]()
![]()
![]()
![]()
![]()
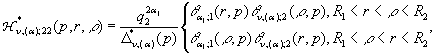
![]() (19)
(19)
![]()
![]()
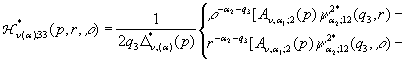
![]()
![]()
Повертаючись в рівностях
(18) до оригіналу, одержимо єдиний розв’язок параболічної задачі (7) – (9) :
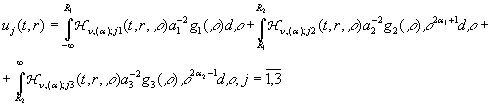 (20)
(20)
У рівностях (20) за означенням [6]
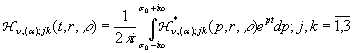 (21)
(21)
Особливими точками
функцій ![]() є точки галуження
є точки галуження ![]() та
та ![]() . Нехай
. Нехай ![]() . Покладемо
. Покладемо ![]() . Тоді при
. Тоді при ![]() маємо:
маємо: ![]() Звідси випливає, що
Звідси випливає, що ![]()
Якщо скористатись методом контурного інтеграла, лемою Жордана й
теоремою Коші [6], то формули (21) можна перетворити до розрахункових:
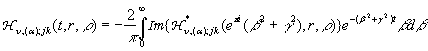 (22)
(22)
Тут ![]() означає уявну частину
від виразу
означає уявну частину
від виразу ![]() .
.
На підставі формул обходу [7]![]()
![]()
знаходимо співвідношення:
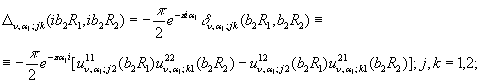
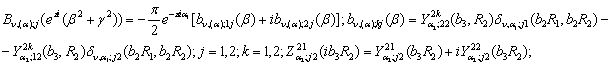
![]()
![]()
![]()
![]()
![]()
У
цих рівностях беруть участь функції:
![]()
![]()
![]() ,
,
![]() .
.
![]() Після низки елементарних перетворень згідно формули (22)
маємо:
Після низки елементарних перетворень згідно формули (22)
маємо:
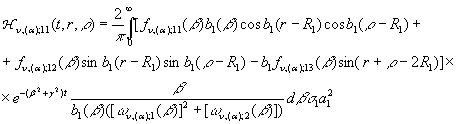 (23)
(23)
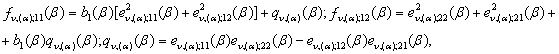
![]()
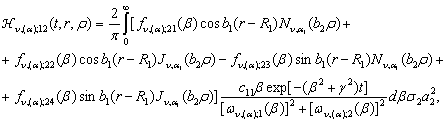 (24)
(24)
![]()
![]()
![]()
![]()
![]()
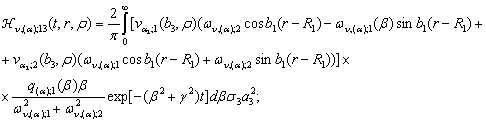 (25)
(25)
![]()
![]()
Якщо
вимагати для ![]() виконання рівностей:
виконання рівностей:
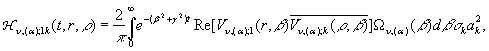 (*)
(*)
то для визначення величин ![]() та
та ![]() (формули (6),
(формули (6), ![]() ) одержимо алгебраїчну систему із 11-ти рівнянь:
) одержимо алгебраїчну систему із 11-ти рівнянь:
![]()
![]()
![]()
![]() (26)
(26)
![]()
Із
алгебраїчної системи (26) при ![]() знаходимо, що
знаходимо, що
![]()
![]()
![]() (27)
(27)
![]()
![]()
![]()
![]()
![]() Згідно формули (6)
компоненти
Згідно формули (6)
компоненти ![]() комплекснозначної спектральної функції
комплекснозначної спектральної функції ![]() визначені:
визначені:
![]()
![]()
![]()
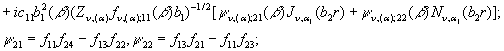 (28)
(28)
![]()
![]()
![]()
З цим комплексно значна вектор-функція ![]() визначена.
визначена.
Введемо до розгляду вагову функцію
![]()
![]()
![]()
У формулах (*) ![]() означає дійсну
частину виразу
означає дійсну
частину виразу ![]() , а риска зверху –
комплексне спряження.
, а риска зверху –
комплексне спряження.
Розв’язок параболічної задачі (20)
набуде вигляду:
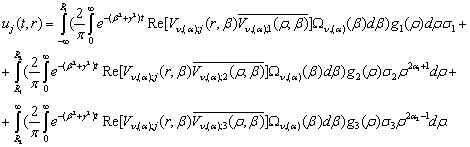 (29)
(29)
![]()
В силу початкових умов отримуємо
інтегральні зображення:
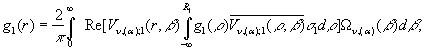
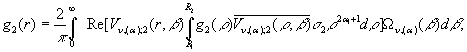
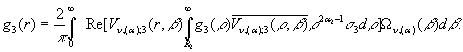
Звідси маємо інтегральне зображення вектор-функції
![]() :
:
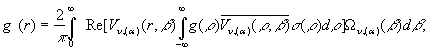 (30)
(30)
Тут
бере участь вагова функція
![]()
Інтегральне
зображення (30) визначає пряме ![]() та обернене
та обернене ![]() гібридне інтегральне
перетворення (ГІП), породжене на декартовій осі ГДО
гібридне інтегральне
перетворення (ГІП), породжене на декартовій осі ГДО ![]() [8]:
[8]:
![]() (31)
(31)
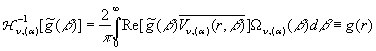 (32)
(32)
В
основі застосування запровадженого формулами (31), (32) ГІП знаходиться основна
тотожність інтегрального перетворення ГДО ![]() .
.
Теорема (про основну тотожність).
Якщо вектор-функція ![]() неперервна на множині
неперервна на множині
![]() , а функції
, а функції ![]() задовольняють умови
обмеженості
задовольняють умови
обмеженості
![]()
![]()
та умови спряження
![]() ,
,
то справджується основна тотожність ГІП
ГДО ![]() :
:
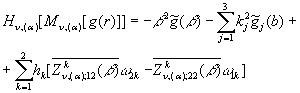 (33)
(33)
У рівності (33) прийняті
позначення:
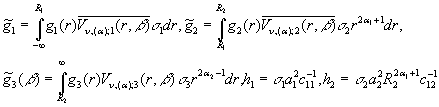
![]()
Застосування запровадженого формулами
(31), (32) ГІП Фур’є– Бесселя – Ейлера на декартовій осі до відповідних задач
математичної фізики подамо в іншій роботі.
Література:
1. Шилов Г.Е. Математический
анализ. Второй специальный курс.- М.: Наука, 1965.-328с.
2.Степанов В.В. Курс
дифференциальных уравнений. - М.:Физматгиз, 1959.-468с.
3.Ленюк М.П. Исследование основных
краевых задач для диссипативного
волнового уравнения Бесселя. – Киев, 1983. – 62с. – (Препринт / АН УССР. Ин-т
математики; 83.3).
4. Ленюк М.П.,
Шинкарик
М.І. Гібридні інтегральні перетворення (Фур’є, Бесселя, Лежандра).
Частина1.- Тернопіль: Економ.думка, 2004.-368с.
5.
Тихонов А.Н., Самарський А.А. Уравнения математической физики. – М.: Наука,
1972. – 735с.
6. Лавренеьев
М.А., Шабат Б.В. Методы теории функций комплексного переменного.
– М.: Наука, 1987. – 688с.
7. Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм,
рядов и произведений. – М.: Наука, 1971. – 1108с.
8. Ленюк М.П. Гібридні
інтегральні перетворення типу Ейлера –
(Фур’є, Бесселя).- Чернівці: Прут, 2009.-76с.