Kumykova Ò., Kumykov V.
(East
Kazakhstan State Technical University, Ust-Kamenogorsk, Kazakhstan)
NATURE
OF THE MOVEMENT OF COMPRESSED AIR ON SHAFT PIPELINES
Movement of compressed air in a coal shaft network
obeys the laws of the turbulence of compressible media. Moreover, the main
factor determining the behavior of turbulent flow, and in particular the laws
of resistance, is the roughness of the pipeline, depending on the material of
which the pipe is made of.
Since pneumatic energy complex of underground mines
are complex systems, experiments with such systems in order to determine their
optimal parameters are costly, time-consuming, and demand violation of
production flow.
Mathematical modelling is based on the identity of the
equations describing the processes of the model and of the studied phenomenon.
The mathematical model of pneumatic energy complex, given the explicitly of a
temporary nature of processes occurring in a pneumatic system, can be
represented in the form of differential equations, reflecting the change in the
basic parameters over time.
The problem of turbulence, which attracts the
attention of scientists over the years which have passed since the appearance
of O. Reynolds’ studies, currently is still far from its full resolution, despite
the large number of published studies and its increasing practical value.
The main characteristic of turbulent flow is a messy,
chaotic nature of turbulent fluctuations. Since the turbulent velocity
fluctuations, rapidly changing from one point to another and from one instant
to the next, are too complicated to be studied in detail, it should be enough
to study only some averaged variables.
While studying the turbulent flow of a compressible
medium, in addition to the correlation between the velocity components, the
relationship between speed and density and the ratio between pressure and
velocity also should be investigated. This greatly complicates the analysis.
According to the law of hydrodynamics of a
compressible medium, the flow of compressed air in a pipeline is fully
described by the equations of motion, energy, continuity and state. Basic
equations of hydrodynamics for a viscous compressible medium / 1 / are as
follow:
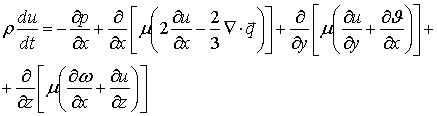 (1)
(1)
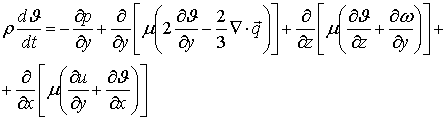 , (2)
, (2)
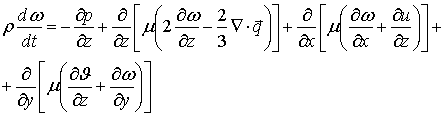 , (3)
, (3)
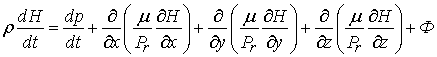 , (4)
, (4)
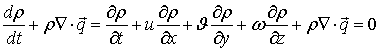 ,
(5)
,
(5)
Ð=r×R×Ò (6)
where
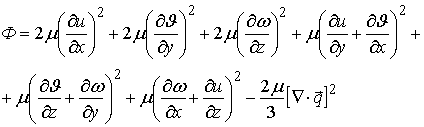 =
=
dissipation function, (7)
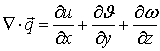 ,
,
![]() - Velocity vector
with components u, w and J along the axes x, y and z, respectively;
- Velocity vector
with components u, w and J along the axes x, y and z, respectively;
T - the instantaneous temperature;
r - instantaneous value of density;
p - instantaneous pressure;
m - dynamic viscosity
coefficient;
Í - enthalpy per unit mass of compressed air (Í= Ñð× Ò,
where Cp - specific heat of air at the isobaric process);
R
- universal gas constant variable;
Pr - Prandtl number of medium.
Equations (1) - (3) represent the equations of motion,
(4) - the energy equation (5) - the continuity equation, (6) - the equation of
state.
Studying turbulence in a compressible viscous medium,
we assume that the instantaneous measures – velocity components u, w and J, of pressure
p, of density r, and of temperature T satisfy the fundamental
equations (1)-(6).
Osborne Reynolds first introduced basic statistical
concepts when studying the turbulent flow. In his theoretical study of
turbulence, he admitted that the instantaneous velocity can be divided into the
average velocity and turbulent fluctuation of velocity.
Therefore we can
assume that
u = `u + u¢ , Ò = `Ò + Ò¢ etc. , (8)
where the bar over the symbol denotes the average
value, and stroke - turbulent
fluctuations.
Direct substitution of equation (8)
in the fundamental equation (1) - (6) does not provide any simple and direct
conclusions about the field of perturbation u¢, Ò¢ etc. due
to the nonlinearity of these equations.
To reveal the nature of the fields
with very small fluctuations in a viscous compressible medium, it should be
resorted to some simplifying assumptions. The first obvious assumption - it is
the assumption of small pulsations, allowing linearizing fundamental equations.
In order to show that small
pulsations in a viscous compressible medium can be divided into three
independent form, Kovazhny /2/ made the following assumptions: -
Specific heat of air ÑP and ÑV, coefficient
of viscosity m, coefficient of thermal conductivity of the medium![]() are
constant;
are
constant;
- Prandtl number Ðr = ÑÐ × m / À equals 3/4;
- The considered
region of space and time is a finite region G. There are no solid boundaries inside the region or on its
borders;
-
Coordinate system is chosen so that the average rate in G is equal to zero;
- The speed is
small compared to an average speed of sound in G;
-
Pulsations of pressure ð¢, density r¢ and absolute temperature T ¢ are small compared with the corresponding average
values of these quantities ð, `r and T in region G.
With
these assumptions and introducing the following dimensionless quantities:
![]() (9)
(9)
And ![]() (10)
(10)
Where 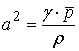
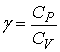 - Ratio of specific heats,
- Ratio of specific heats,
the fundamental equations (1) - (6) can be simplified
and put into the following form:
equation of motion
![]() (11)
(11)
where
grad – is the gradient operator;
div – is
divergence operator;
energy equation
![]() , (12)
, (12)
continuity equation
![]() , (13)
, (13)
equation of state
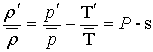 , (14)
, (14)
Where ![]() and
and 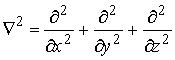 .
.
Equations (11) - (14) are general in nature and as
such can not be applied to study the interaction parameters of the shaft pneumatic
network.
In each theory when solving a task some assumptions
are made. Therefore, comparing the theoretical predictions with experimental
results, it is necessary to trace how assumptions made in the theory are
satisfied in the experimental setup.
Taking as a theoretical basis for research Reynolds
equation (1), (2), (3), it is necessary to know the experimental values that
characterize the mean motion. Indications of anemometer give no direct value of
the average velocity, but a mean value of the function J (x, t) (such
as J2 and others).
The value of velocity and its direction in the horizontal plane are usually
measured.
According
to the equation of Darcy-Veysbakh in the case of the flow of compressed air
along the x-axis the equation of motion can be represented as:
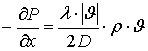 (15)
(15)
where P (x, t) - function of the pressure of
compressed air;
J (x, t) - function of the velocity of compressed air;
r (x, t) - function of density of compressed air;
l - coefficient
of hydraulic resistance of pipeline;
D - diameter of
the pipeline sector;
x - axis, located
along the axis of the pipeline.
In
practice of calculation of shaft pneumatic networks, instead of function of
velocity, such concepts as volume or mass velocity are used.
Given
the fact that
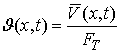 (16)
(16)
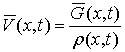 (17)
(17)
Where`V (õ,t)
- function of the volume velocity of the compressed air;`
G (õ,t) -
function of mass velocity of the compressed air;`
FÒ -
cross-sectional area of the pipeline
expression (15) is transformed into
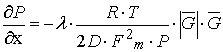 (18)
(18)
Where
Ò (õ,t) – function of absolute temperature
of compressed air;
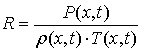
-
universal gas constant.
The equation of continuity according to / 1 / has the
form:
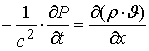 (19)
(19)
Where c - speed of sound in air;
t – time.
Given these relationships, equation (19) can be
transformed into
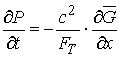 (20
(20
Since
compressed air flows along the x-axis, and the amount of heat entering a unit
volume of compressed air per unit time due to radiation or any other reason,
than the thermal conductivity is zero, as well as the fact that
![]() (21)
(21)
energy
equation (4) can be transformed to the form
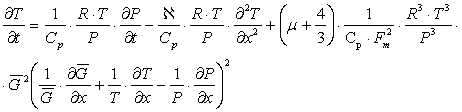 (22)
(22)
Condition of air (6) on a linear plot can be
represented as a function
Ð(õ,t) = R×r(õ,t) × T(õ, (23)
For
practical use of the expression (23) in the problem it is advisable to
differentiate it in respect to x
![]() (24)
(24)
Thus, as
a result of mathematical modelling a system of differential equations with
partial derivatives: (18), (20), (22) and (24) was derived, which fully describes
the distribution and interrelationship of the main parameters of compressed air
along the axis of the pipeline in time. The boundary conditions of application
of this model are as follows:
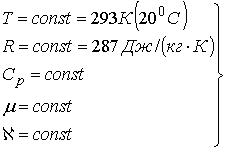 throughout the pipeline;
throughout the pipeline;
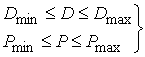 according to the technical conditions of the mine
according to the technical conditions of the mine
(Dmin =50 ìì; Dmax = 400 ìì; Ðmin ³ Pïàñï. ³ 0,5 ÌÏà; Ðmax £ Pêñ = 0,7 ÌÏà).
Air
consumption through the sectors of pneumatic network ![]() = 1 ì: Qi = 0,1¸4,5 ì3/ñ.
= 1 ì: Qi = 0,1¸4,5 ì3/ñ.
References:
1. Jaworski
B.M., Detlaf A.A. Handbook of Physics. -
M.: Nauka, 1984. - 430 pp.
2. Bai Shi Yi Turbulent Flows of Liquids and Gases / / Translation from
English Ph.D. MG Morozov / Edited by Dr. K.D. Voskresensky. - Moscow: Foreign
Literature, 1982. - 344 pp.