Д.ф.-м.н. Божанов Е.Т.
Казахский национальный технический университет им.К.Сатпаева, Казахстан
Д.т.н. Отарбаев Ж.О.
Казахский национальный технический университет им.К.Сатпаева, Казахстан
К.т.н. Буганова С.Н.
Международная образовательная корпорация (Казахская головная
архитектурно-строительная академия), Казахстан
ГИБКОСТЬ РЫХЛЕННОЙ ЗОНЫ ВЫРАБОТКИ ПО ГЛАВНЫМ НАПРАВЛЕНИЯМ
МЯГКОЙ МАТРИЦЫ
Рассмотрим
одиночную выработку толщиной h как стационарный объект с запаздывающим
аргументом мягкой матрицы и действием
высокого давления со стороны рудного материала q0.
Уравнения равновесия имеет вид согласно [1]-[3].
![]() (1)
(1)
где 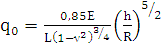 , ξ=
, ξ=![]() , X=λξ-t (2)
, X=λξ-t (2)
h- толщина, L-длина,
R-внутренний радиус.
Здесь возможны случаи:
I-случай ![]() , корни
характеристического уравнения:
, корни
характеристического уравнения:
![]() ;
; ![]() ; α=
; α=![]()
II-случай ![]() , корни
характеристического уравнения:
, корни
характеристического уравнения:
![]() ;
; ![]() ; α=
; α=![]() ;
; 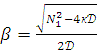
III-случай ![]() , корни
характеристического уравнения:
, корни
характеристического уравнения:
![]() ;
; ![]() ;
;
r=![]() ; φ=
; φ=![]() ;
; ![]() ; β=
; β=![]()
Рассмотрим II-случай ![]() , при граничных условиях
, при граничных условиях
![]() ,
(3)
,
(3)
![]() (4)
(4)
Общее решение (1) ищем в
виде
W(![]() )=W0(
)=W0(![]() )+W1(
)+W1(![]() ) (5)
) (5)
где W0(![]() )- есть общее решение
однородной части, а W1(
)- есть общее решение
однородной части, а W1(![]() ) - частное решение.
) - частное решение.
Тогда для
решения поставленной задачи предположим, что матрица с высокой вязкостью
наполнена частицами вещества типа свинца, угля, алюминия, железа или меди и др.
рудного материала, а рассеивание механической энергии, вследствие вязкого
течения, взаимодействует с непрерывным упругим упрочненным волокном рыхленного
слоя. Вследствие этого адиабатические изменения объема dQ - очень медленные
изотермические изменения объема dT обусловлены наложенным гидростатическим
давлением без наличия объемной вязкости в промежуточных процессах [3]-[4].
При таких
предположениях:
линейные
перемещения W (как общее решение (1))
определяются:
![]() (6)
(6)
угловые перемещения
θ:
![]() (7)
(7)
изгибающие моменты – М:
М=-ЕJ![]() (8)
(8)
перерезывающие силы – Q:
![]() (9)
(9)
Подставляя (6)–(9) в
граничные условия (3)–(4) имеем систему алгебраических уравнении для
определения постоянных С1, С2,
С3, С4:
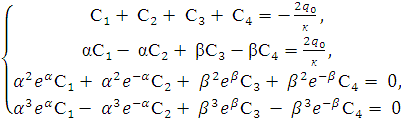 (10)
(10)
Система (10) имеет
единственное решение:
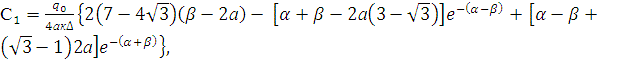
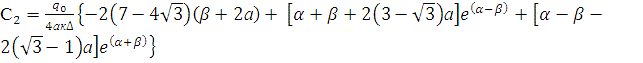 ,
,
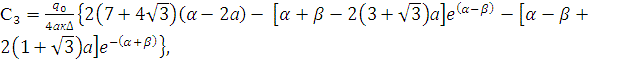
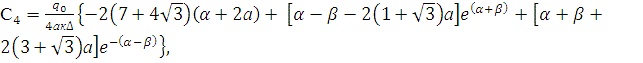
![]() (11)
(11)
Подставляя (11) в
уравнение (6) получим:
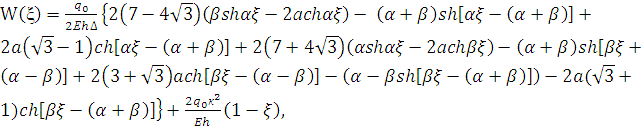 (12)
(12)
где ![]()
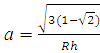 , α=
, α=![]() ,
,
β= ![]() ,
, ![]() (13)
(13)
Если главные направления
рыхленной зоны направлены не по ортогональным направлениям, а по геодезическим
линиям, то уравнение равновесие имеет вид:
![]() , (14)
, (14)
а линейные и угловые
перемещения, изгибающие моменты, перерезывающие силы в смежных сечениях будут
(без множителя ЕJ):
W(ξ)=![]() , (15)
, (15)
![]() =
= ![]() , (16)
, (16)
![]()
![]() , (17)
, (17)
![]() (18)
(18)
Поставляя (15)-(18) в
граничные условия (3)-(4):
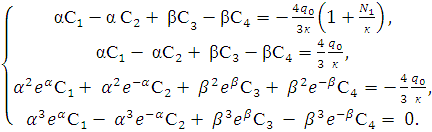 (19)
(19)
Система (19) имеет
единственное решение. Решая систему (19) определим С1,С2,С3,С4,
затем подставляя их значения в уравнение (15) получим:
W(ξ)=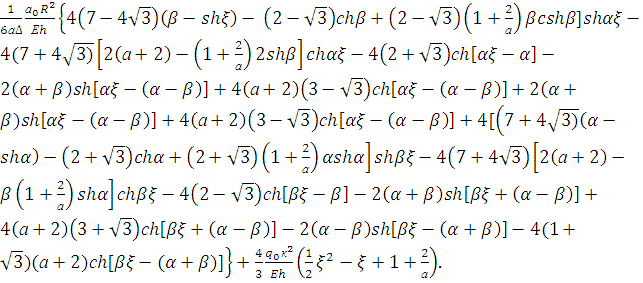 (20)
(20)
где ![]() определяются формулами (13).
определяются формулами (13).
С помощью программирования в
системе Матлаб
были получены следующие результаты:
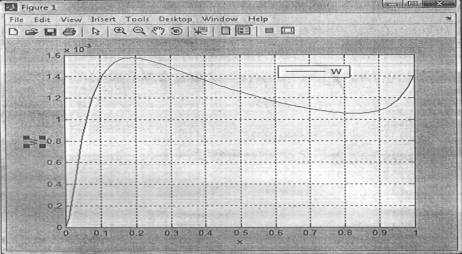
Рисунок
1. Изменение гибкости резервуара мягкой матрицы
На рисунке 1
показано изменение гибкости рыхленной зоны выработки по главным направлениям,
когда упрочнение рыхленной зоны осуществляется с учетом релаксации, а матрица
наполнена частицами типа свинца, алюминия, угля, железа или медных сплавов и
других рудных материалов.
Литература:
1.
Буганова С.Н., Отарбаев Ж.О., Божанов Е.Т. Об
одной модели определения устойчивости, выпучивания и колебания тонкостенных
конструкций в «новом начале», как стационарного объекта с запаздывающим
аргументом // Найновите научни постижения: материали за V
Межд. науч.-практ. -Т.24 Технологии. – София, 2009. - С.28-32.
2.
Сыркин В.Г. Материалы будущего: О нитевидных кристаллах металлов.
Академия наук СССР. - М.: Наука, 1990. - 192 с.
3.
Партон
В. 3. Механика разрушения: От
теории к практике.— М.: Наука. Гл. ред. физ.-мат. лит., 1990.- 240 с.
4.
Жумагулов Б.Т., Евсеева А.У., Евсеев О.О.,
Карсакбаев А.А. Математическое и компьютерное моделирование в задачах
трубопроводного транспорта//Вестник НИА РК. -
2008. - №3(29).
5.
Буганова С.Н., Отарбаев Ж.О., Божанов Е.Т.
Теоретико-проектные расчеты напряженно-деформированного состояния и
устойчивости выработки произвольного сечения в условиях эксплуатации//Новости
передовой науки. -Т.18 Технологии. – София, 2009. - С.3-6.