1.Дифференциальные и интегральные уравнения
Ж.Б. Муканов
Евразийский национальный университет им. Л.Н.Гумилева,
г.Астана
О НЕОБХОДИМОМ УСЛОВИИ ИНТЕГРИРУЕМОСТИ
СО СТЕПЕННЫМ ВЕСОМ ФУНКЦИИ, ПРЕДСТАВЛЕННОЙ МОНОТОННО УБЫВАЮЩИМ ОБОБЩЕННЫМ МУЛЬТИПЛИКАТИВНЫМ ПРЕОБРАЗОВАНИЕМ
Пусть
![]() , где
, где ![]()
![]() ,
,
- произвольная бесконечная в обе стороны последовательность натуральных чисел, а
![]() ,
,
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() , соответствующая ей группа с групповой операцией
, соответствующая ей группа с групповой операцией ![]() .
.
Рассмотрим группу ![]() , определяемую последовательностью
, определяемую последовательностью ![]() , симметричной последовательности
, симметричной последовательности ![]() , т.е.
, т.е.
![]() , где
, где ![]() .
.
Группу ![]() образуют
последовательности
образуют
последовательности
![]() ,
,
где ![]() ,
, ![]() ,
, ![]() .
.
Для каждой пары ![]() определим функцию
двух переменных
определим функцию
двух переменных ![]() :
:
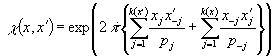 . (1)
. (1)
Множество таких функций назовем обобщенной мультипликативной
системой.
Введем обозначения:
![]() ,
, ![]() ,
, 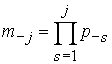 , .
, .![]() .
.
Учитывая симметричность ![]() имеем
имеем
![]() ,
, 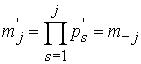 ,
, 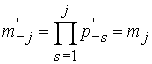 ,
, ![]() .
.![]()
Каждую из групп ![]() и
и ![]() отобразим на
действительную полуось. Для этого последовательности
отобразим на
действительную полуось. Для этого последовательности ![]() поставим в
соответствие ряд
поставим в
соответствие ряд
![]() , (2)
, (2)
а последовательности ![]() - ряд
- ряд
![]() . (3)
. (3)
Здесь ![]() означает целую часть
числа
означает целую часть
числа ![]() , а
, а ![]() - дробную часть числа
- дробную часть числа
![]() .
.
Соответствие между лучом ![]() и группой
и группой ![]() (а также между
(а также между ![]() и группой
и группой ![]() ) будет взаимно-однозначным, если каждая
) будет взаимно-однозначным, если каждая ![]() -ично- рациональная (соответственно
-ично- рациональная (соответственно ![]() -ично - рациональная) точка считается дважды.
-ично - рациональная) точка считается дважды.
Таким образом, построенная система функций
![]() является
континуальным аналогом системы Прайса [1].
является
континуальным аналогом системы Прайса [1].
Более подробные сведения о континуальных
аналогах ![]() изложены в монографии
[1].
изложены в монографии
[1].
Двумерные системы функций ![]() определим равенством
определим равенством
![]() .
.
Обозначим через ![]() - пространство
измеримых на
- пространство
измеримых на ![]() по мере Лебега
функций
по мере Лебега
функций ![]() с конечной нормой
с конечной нормой
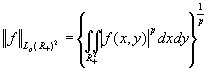 .
.
Обобщенное мультипликативное
преобразование Фурье функции ![]() определяется
равенством
определяется
равенством
![]() .
.
Для функции ![]() прямым
мультипликативным
прямым
мультипликативным ![]() - преобразованием назовем функцию
- преобразованием назовем функцию
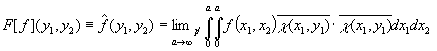
где ![]() .
.
В данной работе исследуются вопросы ![]() –интегрируемости (1<p<∞) со степенным весом функции двух
переменных, представленной через монотонно убывающее обобщенное
мультипликативное преобразование Фурье.
–интегрируемости (1<p<∞) со степенным весом функции двух
переменных, представленной через монотонно убывающее обобщенное
мультипликативное преобразование Фурье.
Сформулируем
определения.
Пусть ![]() а
а ![]() ,
, ![]() - двумерные векторы,
- двумерные векторы, ![]() . Обозначим через
. Обозначим через ![]() =
=![]() множество всех
двумерных векторов, координаты которых равны 0 или 1. Через а
обозначим вектор, все координаты которого равны
множество всех
двумерных векторов, координаты которых равны 0 или 1. Через а
обозначим вектор, все координаты которого равны ![]() (аналогично вектор b). Тогда
(аналогично вектор b). Тогда
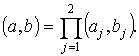
Если векторы ![]() и вектор
и вектор ![]() , то будем говорить, что
, то будем говорить, что ![]() в том случае, когда
в том случае, когда ![]() =0 при
=0 при ![]() и
и ![]() при
при![]() , имеем
, имеем ![]()
Говорят, что функция ![]() монотонна по Харди,
т.е.
монотонна по Харди,
т.е. ![]() , где
, где ![]() ,
, ![]() и
и ![]() , (см.[2]), если
, (см.[2]), если ![]() и для любого
ненулевого вектора
и для любого
ненулевого вектора ![]() выражение
выражение
![]()
либо неотрицательно при всех ![]()
![]() либо неположительно
при таких
либо неположительно
при таких ![]()
Ядро Дирихле для двумерного случая имеет
вид
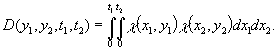 (4)
(4)
В следующей теореме приводится достаточное
условие интегрируемости со степенным весом функции ![]() . При этом условие выражено в терминах обобщенных
мультипликативных преобразований.
. При этом условие выражено в терминах обобщенных
мультипликативных преобразований.
Теорема
1. Пусть 1<p<∞, 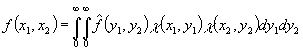 , где
, где![]() , существуют частные производные
, существуют частные производные ![]() ,
, ![]() и
и ![]() ,
, ![]() ,
, ![]() . Тогда, если
. Тогда, если
![]() ,
,
то
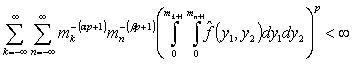 , (5)
, (5)
Для доказательства приведенной теоремы нам
понадобятся следующие вспомогательные утверждения.
Лемма
А. (см.[3]). Пусть обобщенное ядро Дирихле
![]() определено равенством (4). Тогда
определено равенством (4). Тогда
а) Для любых ![]() и m, n
и m, n ![]() Z имеет место равенство
Z имеет место равенство
![]() ,
,
где ![]() - характеристическая функция
- характеристическая функция ![]() .
.
б) ![]() для
для ![]() ,
, ![]()
Лемма
1. Если ![]() , где
, где ![]() , существуют частные производные
, существуют частные производные ![]() ,
, ![]() и
и
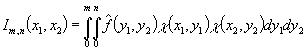 , m,n
, m,n![]() Z+ ,
Z+ ,
то ![]() и
и ![]() имеет место неравенство
имеет место неравенство
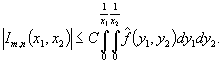 (6)
(6)
Лемма 1
доказывается с помощью применения формулы интегрирования по частям и леммы А.
Лемма
B. (Moricz F., [4]). Пусть 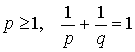 ,
, ![]() функция
функция ![]() ≥0
определена для
≥0
определена для ![]() и
и
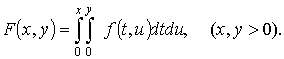
Тогда, если
![]()
то
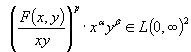
и
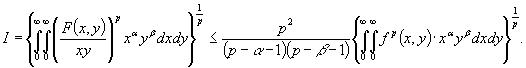
Доказательство теоремы 1.
Так как
![]()
и
![]() ,
,
то на основании неравенства Гельдера имеем
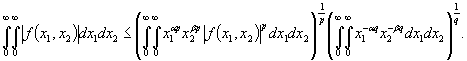
Следовательно,
![]() и согласно
и согласно
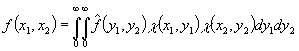
и (4), а также леммы А
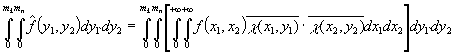 =
=
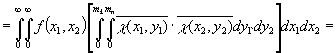
=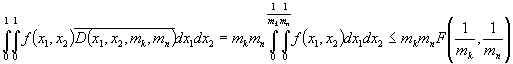 , (7)
, (7)
где
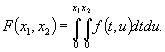
По лемме B
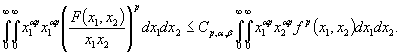 (8)
(8)
С другой стороны в силу монотонности ![]() и оценки (7)
имеем, что
и оценки (7)
имеем, что
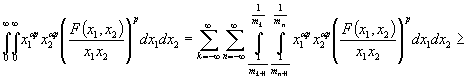
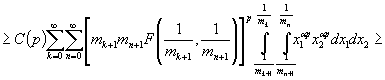
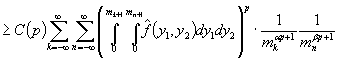 .
.
Так как по условию теоремы ![]() и учитывая (8),
то
и учитывая (8),
то
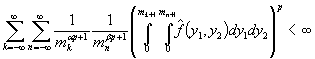 .
.
Теорема 1 доказана.
Литература
1.
Голубов Б.И., Ефимов
А.В., Скворцов В.А. Ряды и преобразования Уолша. Теория и применения. -
М.:Наука. Гл. ред. физ.-мат. лит., 1987.-344 с.
2.
Дьяченко М.И. Кусочно монотонные
функции многих переменных и теорема Харди–Литтлвуда // Изв. АН СССР. Сер. мат. – 1991.– Т.55, № 6.– С . 1156–1170.
3.
Голубов Б.И. Элементы двоичного анализа. М.:МГУП, 2005. – 204 с.
4.
Moricz F. On double cosine, sine, and Walsh series with monotone coefficients. //
Proc. Amer. Math. Soc.– 1990.– V.109. № 2.– P. 417 – 425.