Шилинец В. А., Кравченко И. Н., Рылова А. С., Скодорво О. З.

Белорусский государственный педагогический университет

ИССЛЕДОВАНИЕ КРАЕВОЙ ЗАДАЧИ ДЛЯ КВАТЕРНИОННЫХ ФУНКЦИЙ ТРЕХ ДЕЙСТВИТЕЛЬНЫХ ПЕРЕМЕННЫХ

В. А. Гусев в работе [1] изучал кватернионные моногенные в смысле
В. С. Федорова (F-моногенные) функции [2] на плоскости. В работах [3–5] исследовались кватернионные функции трех и четырех действительных переменных.

В данной работе исследуются F-моногенные кватернионные функции, отличные от ранее рассмотренных. Для этих кватернионных функций получено интегральное представление и решена краевая задача.

Пусть – односвязная область трехмерного действительного евклидова пространства .

Рассмотрим кватернионные функции вида

, ,

где – действительные функции класса , – базис алгебры кватернионов (

), – такие действительные числа, что .

Для любых точек и области полагаем

, .

Определение. Кватернионная функция называется моногенной в смысле В. С. Федорова (F-моногенной) [2] по кватернионной функции в области , если существует такая кватернионная функция

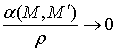( – однозначные действительные функции точки () области ), что для любой фиксированной точки и любой переменной точки имеем , где при , .

Легко показать, что если функция – F-моногенная по функции в области , то существуют частные производные 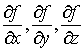, и при этом

.

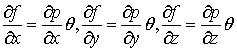Рассмотрим следующую краевую задачу.

Задача. Пусть – трехмерная ограниченная область с границей (). Полагаем далее, что и функция , F-моногенная по , определены на замкнутой двумерной поверхности , гомеоморфной сфере конечного диаметра и достаточно гладкой для возможности использовать формулу Остроградского. Требуется найти в любой внутренней точке области значение функции , F-моногенной по , если известны ее значения на поверхности .

Для функции и произвольной точки полагаем [6]:

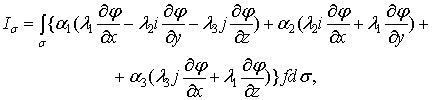(1)

где – направляющие косинусы внешней нормали к поверхности в ее текущей точке , ,

.

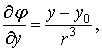
Доказаны следующие теоремы.

Теорема 1. Пуст – любая точка области , . Для любой кватернионной функции , F-моногенной по кватернионной функции в области , имеем , где определяется равенством (1).

Теорема 2. Если кватернионная функция является F-моногенной по кватернионной функции в области , то для любой точки , лежащей внутри , имеем

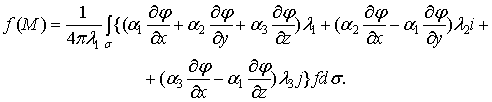(2)

С помощью полученного интегрального представления (2) и решается сформулированная краевая задача.

Литература:

1. Гусев В.А. О кватернионных функциях, моногенных в смысле В.С.Фёдорова // Успехи математических наук, 1965.– Т. 20, вып. 1(121).– С. 203-208.

2. Фёдоров В.С. Основные свойства обобщённых моногенных функций // Известия вузов. Математика, 1958.– №6.– С. 257-265.

3. Стэльмашук М.Т., Шылінец У.А. Аб інтэгральным выяўленні кватэрніённых F-манагенных функцый аднаго класа // Весці БДПУ. Серыя 3, 2005.–№2.– С. 8-10.

4. Стэльмашук М.Т., Шылінец У.А., Падабед Г.Ф. Рашэнне краявой задачы для кватэрніённых функцый чатырох рэчаісных зменных // Весці БДПУ. Серыя 3, 2006.–№1.– С. 12-14.

5. Стэльмашук М.Т., Шылінец У.А., Андрэева Г.А. Аб кватэрніённых манагенных у сэнсе У.С. Фёдарава функцыях // Весці БДПУ. Серыя 3, 2010.–№1.– С. 11-13.

6. Фёдоров В.С. Об одном обобщении интеграла типа Коши в многомерном пространстве // Известия вузов. Математика, 1957.– №1.– С. 227-233.