М.П. Ленюк
Чернівецький
факультет НТУ «ХПІ»
СКІНЧЕННЕ
ГІБРИДНЕ ІНТЕГРАЛЬНЕ ПЕРЕТВОРЕННЯ ТИПУ
БЕССЕЛЯ-(КОНТОРОВИЧА-ЛЄБЄДЄВА)-ФУР´Є НА СЕГМЕНТІ ![]() ПОЛЯРНОЇ ОСІ.
ПОЛЯРНОЇ ОСІ.
Запровадимо
інтегральне перетворення, породжене на множині ![]() гібридним
диференціальним оператором (ГДО)
гібридним
диференціальним оператором (ГДО)
![]() (1)
(1)
Тут ![]() - одинична функція Гевісайда,
- одинична функція Гевісайда, ![]() - диференціальний оператор Бесселя [2],
- диференціальний оператор Бесселя [2], ![]() - диференціальний оператор (Конторовича-Лєбєдєва) [3];
- диференціальний оператор (Конторовича-Лєбєдєва) [3]; ![]() =
=![]()
Означення. Областю задання ГДО ![]() назвемо множину G вектор-функцій
назвемо множину G вектор-функцій ![]() з такими властивостями:
з такими властивостями:
1) вектор-функція ![]() неперервна на множині
неперервна на множині![]() ;
;
2) функції ![]() задовольняють крайові умови
задовольняють крайові умови
![]()
![]() (2)
(2)
3) функції ![]() задовольняють умови
спряження
задовольняють умови
спряження
![]() (3)
(3)
Оскільки ГДО ![]() самоспряжений і на множині
самоспряжений і на множині ![]() не має особливих
точок, то його спектр дійсний і дискретний [4]. Якщо
не має особливих
точок, то його спектр дійсний і дискретний [4]. Якщо ![]() - спектральний параметр, то йому відповідає спектральна
вектор-функція
- спектральний параметр, то йому відповідає спектральна
вектор-функція
![]() (4)
(4)
При цьому функції ![]() повинні задовольняти відповідно
диференціальні рівняння
повинні задовольняти відповідно
диференціальні рівняння
![]()
![]() (5)
(5)
![]()
крайові умови (2) та умови спряження (3).
Якщо
вважати, що
![]()
![]() (6)
(6)
![]()
то для визначення п´яти
величин ![]() та
та ![]() крайова умова в точці
крайова умова в точці
![]() та умови спряження (3)
дають однорідну алгебраїчну систему з п´яти рівнянь:
та умови спряження (3)
дають однорідну алгебраїчну систему з п´яти рівнянь:
![]()
![]() (7)
(7)
![]()
Введемо до розгляду функції:
![]()
![]()
![]()
![]()
Алгебраїчна система (7) має ненульові
розв´язки тоді й тільки тоді, коли визначник системи дорівнює нулю:
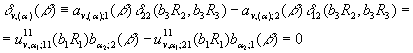 (8)
(8)
Ми
одержали трансцендентне рівняння для обчислення власних чисел ![]() ГДО
ГДО ![]() . Підставимо
. Підставимо![]() в алгебраїчну систему (7) й відкинемо останнє рівняння в
силу лінійної залежності;
в алгебраїчну систему (7) й відкинемо останнє рівняння в
силу лінійної залежності; ![]()
Розглянемо
алгебраїчну систему стосовно ![]() при
при ![]()
![]()
Звідси
знаходимо, що
![]()
![]()
![]()
При
відомих ![]() розглянемо
алгебраїчну систему стосовно
розглянемо
алгебраїчну систему стосовно ![]()
![]()
Звідси,
одержуємо, що
![]()
![]()
![]()
![]()
Підставивши
визначені ![]() у рівності (6), маємо
функції:
у рівності (6), маємо
функції:
![]()
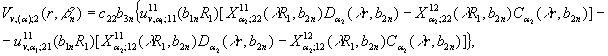
![]() (9)
(9)
Отже,
вектор-функція ![]() визначена.
визначена.
Визначимо
числа
![]()
вагову функцію
![]()
та квадрат норми власної функції
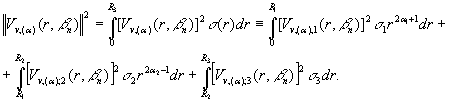
Згідно з роботою [5]
наведемо твердження.
Теорема 1 (про дискретний спектр).
Корені ![]() трансцендентного рівняння
трансцендентного рівняння ![]() складають дискретний спектр ГДО
складають дискретний спектр ГДО ![]() : дійсні, різні, симетричні відносно
: дійсні, різні, симетричні відносно ![]() й на піввісі
й на піввісі ![]() утворюють монотонно зростаючу числову
послідовність з єдиною граничною точкою
утворюють монотонно зростаючу числову
послідовність з єдиною граничною точкою ![]()
Теорема 2 (про дискретну функцію). Система власних функцій ![]() ортогональна на
множині
ортогональна на
множині ![]() з ваговою функцією
з ваговою функцією![]() , повна й замкнена.
, повна й замкнена.
Теорема 3 ( про зображення рядом
Фур'є). Будь-яка ![]() зображається за системою
зображається за системою ![]() абсолютно й
рівномірно збіжним на множині
абсолютно й
рівномірно збіжним на множині ![]() рядом Фур'є:
рядом Фур'є:
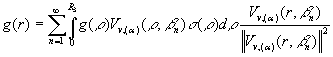 (10)
(10)
Ряд Фур'є (10) визначає пряме![]() й обернене
й обернене ![]() скінченне гібридне інтегральне
перетворення (СГІП), породжене на множині
скінченне гібридне інтегральне
перетворення (СГІП), породжене на множині ![]() ГДО
ГДО ![]() :
:
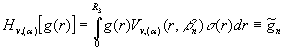 (11)
(11)
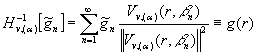 (12)
(12)
Якщо перейти до ортормованої
системи
![]()
то правила (11) та (12) набувають вигляду:
![]() (13)
(13)
![]() (14)
(14)
Теорема 4 (про основну тотожність). Якщо вектор-функція ![]() неперервна на множині
неперервна на множині
![]() , а функції
, а функції ![]() задовольняють крайові умови
задовольняють крайові умови
![]()
![]() (15)
(15)
та умовами спряження
![]() (16)
(16)
то має місце основна тотожність СГІП ГДО ![]()
![]()
+![]() (17)
(17)
Тут прийняті позначення:
![]() ,
,![]()
![]()
![]()
![]()
![]()
Правила (13), (14) та (17)
складають математичний апарат для розв'язування відповідних задач математичної
фізики неоднорідних середовищ.
Логічну схему застосування
запровадженого СГІП покажемо на одній із типових задач.
Задача
(квазістатики). Побудувати обмежений в області
![]()
розв'язок параболічної системи
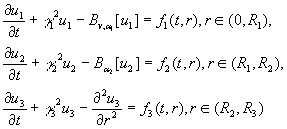 (18)
(18)
за початковими умовами
![]() (19)
(19)
крайовими умовами
![]()
![]() (20)
(20)
та умовами спряження
![]() (21)
(21)
Розв´язання: Запишемо систему (18) й
початкові умови (19) в матричній формі:
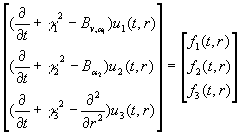 ;
;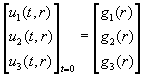 (22)
(22)
Інтегральний оператор ![]() згідно правила (13) зобразимо у вигляді операторної матриці-рядка:
згідно правила (13) зобразимо у вигляді операторної матриці-рядка:
![]() (23)
(23)
Застосуємо операторну матрицю-рядок
(23) за правилом множення
матриць до задачі (22). Внаслідок основної тотожності (17) отримуємо задачу
Коші:
![]() (24)
(24)
Тут ![]()
![]()
![]()
![]()
![]()
Розв´язком
задачі Коші (24) є функція
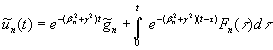 (25)
(25)
Оператор ![]() згідно правила (14)
як обернений до (23) у вигляді операторної матриці-стовпця:
згідно правила (14)
як обернений до (23) у вигляді операторної матриці-стовпця:
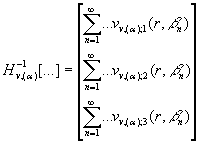 (26)
(26)
Застосуємо за правилом множення
матриць операторну матрицю-стовпець(26)
до матриці-елемента ![]() , де функція
, де функція ![]() визначена формулою (25). У результаті
низки елементарних перетворень отримуємо інтегральне зображення аналітичного розв'язку
параболічної задачі (18)-(21):
визначена формулою (25). У результаті
низки елементарних перетворень отримуємо інтегральне зображення аналітичного розв'язку
параболічної задачі (18)-(21):
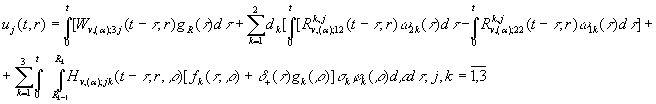
![]() (27) У
рівностях (27) беруть участь головні розв'язки даної параболічної задачі:
(27) У
рівностях (27) беруть участь головні розв'язки даної параболічної задачі:
1) породжені неоднорідністю системи (18) функції
впливу
![]() (28)
(28)
2) породжені неоднорідністю крайової умови в точці
![]() функції Гріна
функції Гріна
![]() (29)
(29)
3) породжені неоднорідністю умов спряження функції
Гріна
![]() (30)
(30)
За
наведеною логічною схемою знаходяться інтегральні зображення аналітичних
розв´язків відповідних еліптичних та гіперболічних задач.
Зауважимо,
що розв´язок (27) носить алгоритмічний характер. Це дозволяє його
використовувати як в теоретичних дослідженнях, так і в числових розрахунках.
Наявність великої кількості параметрів дає змогу безпосередньо із загальних
структур виділити будь-який практично потрібний випадок (у рамках даної
моделі).
Література:
1.
Шилов Г.Е. Математический анализ.
Второй специальный курс. – М.: Наука, 1965. – 328с.
2.
Ленюк М.П. Исследования
основных краевых задач для диссипативного волнового уравнения Бесселя. – Киев,
1983. – 62с. – (Препринт / АН УССР. Ин-т математики; 83.3).
3.
Ленюк М.П., Міхалевська Г.І. Гібридні інтегральні
перетворення типу Конторовича – Лєбєдєва. – Чернівці: Прут, 2002. – 280с.
4.
Ленюк М.П., Шинкарик М.І. Гібридні інтегральні перетворення (Фур’є,
Бесселя, Лежандра). Частина 1. – Тернопіль: Економ. думка, 2004. – 368с.
5.
Комаров Г.М., Ленюк М.П., Мороз В.В. Скінченні гібридні інтегральні
перетворення, породжені диференціальними рівняннями другого порядку. –
Чернівці: Прут, 2001. – 228с.