Спектральный анализ измерительной системы

по инвариантным моделям

 Желонкин А.И. (Московский государственный открытый университет)

Спектральные разложения сигналов и динамических характеристик систем позволяет построить аппарат расчета и проектирования параметрических систем, сводящий выполнение исследований к алгебраическим операциям над числами путем перехода от непрерывных частотных характеристик к временным характеристикам и их разложениям по ортогональным базисам [1,2]. Расчет спектральных характеристик сигналов и систем в базисах тригонометрических проводится с использованием аппарата быстрого преобразования Фурье (БПФ), функции Уолша и полиномов Чебышева.

При синтезе и анализе динамических систем, их детальное описание приводит к исходным уравнениям высокого порядка, решение которых (уже более третьего порядка) представляет значительные трудности и при использовании современной вычислительной техники.

Разработка инвариантных математических моделей позволила свести исследование в спектральной области к определению спектральных характеристик элементарных звеньев, по которым рассчитываются характеристики сигналов и систем. Переход от дифференциальных уравнений к интегральным проведен путем матричного представления интегральных ограниченных операторов в ортогональных базисах.

Для построения структурной схемы при исследовании в спектральной области применяем известный в теории аналогового моделирования метод последовательного непосредственного преобразования и общий метод программирования для уравнений, решаемых относительно старшей производной. Дифференциальное уравнение системы с переменными коэффициентами запишем в виде: 

                            ;                                           (1)

где: x(t) – входной сигнал системы, y(t) –выходной процесс.

Положим, что функции b0(t), b1(t),…, bn-1(t), bn(t) =1,  y0(t) определены и непрерывны на промежутке [0,T]. Уравнение (1) имеет единственное решение y(t) для любого вектора начальных условий Y0 =  y(0),  y'(0), …, y(n-1) (0). Эквивалентные уравнению (1) относительно y(n -1) (t) и y(t) интегральные уравнения определяются последовательным интегрированием. Используя формулу Коши, условия: y(0) = y0,  y’(0) = y1,…, y(n -1) (0) = yn –1, yn (t) = z(t);  и равенство[173]: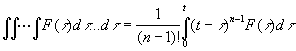, получим:

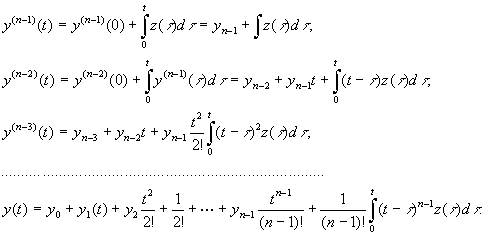                  (2)

 На основании уравнения (1) и учитывая зависимость:

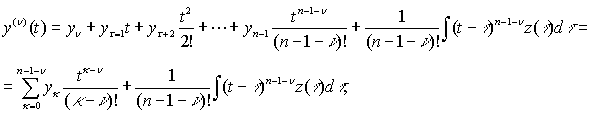
получим следующее выражение для выходного сигнала:

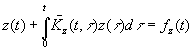                             ;                                                (3)

где: .

Интегрируя уравнение (1) n раз, с учетом равенства (2) получаем:

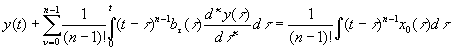     .                Интегрируя левую и правую части (7.4) при нулевых начальных условиях, (4)

находим: 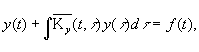                                                                     (5)

где: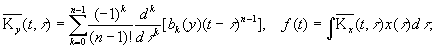                                

2

                  

при этом:

  С учетом функций ограничения получим уравнение Фредгольма 2-го рода:

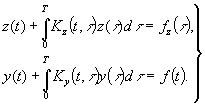                                                                            (6)

Решение уравнения (6) относительно y(t) проводим в виде разложения по ортонормированному базису (ОНБ) Ф(t) в операторной форме. Уравнение (6) запишем в виде:                                                                      (7)

Оператор Ах отображает пространство L2[0,T], которое удобно представить в виде матричных операторов в конечномерных пространствах. Определив ОНБ как: Ф(t)={jk (t) : k=1,…;  t[0, T]} – ОНБ, представим y(t) L2[0,T] в виде разложения по базису Ф(t):                                                         (8)                                               

где 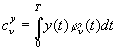 - коэффициенты Фурье.

На основании (7) и (8) запишем:

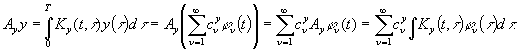             (9)

 Заменяя в (9) все функции их спектральными представлениями, получим:

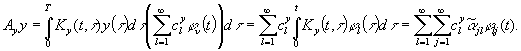      (10)

Для  справедливо:  ;          (11)

На основании (7), (8), (10), (11), запишем:

 Обобщая коэффициенты при функциях jj(t), (j = 1, 2, …)   с одинаковыми индексами, спектральную характеристику относительно ортонормированного базиса Ф´Ф получим в виде матрицы: Ay Cy = Cf.                                                  

Спектральная характеристика Аy  представляет собой матрицу коэффициентов

3

Фурье разложения ядра Ky(t,t) по базису Ф(t) ´ Ф(t):. 

                       .

Матричное  представление  интегральных  операторов с ядрами  Ky(t,t)  и

Kx(t,t) относительно ортонормированного базиса Ф позволяет получить уравнение относительно вектора Сх , которое в матричной форме имеет вид:     

                                                  Аy Сy = Аx Сx ,                                            (12)

где Сх = (сх1, сх2,…, схl,…)T – спектральная характеристика входного сигнала  x(t),

      Ay – матричный оператор форсирующей части системы, определяемый интегральным оператором с ядром Ky(t, t).

На основании (12),  сиcтема описывается уравнением:

                                 Сy = (Ay)-1 Ax Cx = ACx.                                               (13)

Спектральная характеристика системы запишется в виде:

                                                                                                  (14)

Спектральная форма описания системы соотношением (13) связывает три спектральные характеристики: входного сигнала x(t)« Cx , выходного процесса y(t) )« Cy и системы А, определяемой формулой (14).

Представленный спектральный метод реализуется на ЭВМ с использованием алгоритмов БПФ.

Литература:

1. Желонкин А.И. Инвариантный метод исследования динамических систем // Приборы и системы: – 2004. №6. – С. 23 – 27.

2. Желонкин А.И.   Инвариантное моделирование динамических процессов и систем // Естественные и технические науки. – 2008. № 4. – С. 28–31. 

3. Петров Б.Н и др. Принцип инвариантности в измерительной технике. – М.: Наука. – 1976. – 214 с.

 

 

             

 

4

Интегральный метод разработки инвариантной модели

Желонкин А.И. (Московский государственный открытый университет)

 

Анализ особенностей методов разработки упрощенных математических моделей показал, что наиболее удобной для расчетов можно считать обобщенную математическую модель, представляющую собой  аналитическое описание элементарного динамического звена первого или второго порядка.  Исследование системы по такому уравнению не требует отыскания корней сложных уравнений.  Учитывая, что характеристики переходного процесса системы определяют ее динамику, за основу построения модели принимается условие равенства интегральных квадратичных оценок динамических процессов, определяемых по исходному и упрощенному уравнениям [1-3].

Для повышения точности приравниваются не только интегралы от квадрата координаты, но и от ее первых n производных:

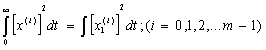                           ;                                  (1)

 где: x, x1 – координаты исходного и аппроксимирующего уравнений, m – порядок полинома аппроксимирующего уравнения пониженного порядка.

Переходную функцию x(t), соответствующую исходной передаточной функции W(p) запишем в виде:

                           (anpn+an-1pn-1+...+ a1p+a0) x(t) = 0;                                  (2)

Аппроксимирующей передаточной функции

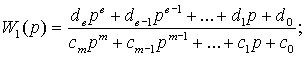                                                           (3)

 соответствует дифференциальное уравнение:

             (cmpm+ cm-1 pm-1+...+c1p+c0) x1(t) = 0;  e < m < n.                          (4)

Учитывая, что переходные  функции  определяются  при  воздействии единичного импульса – K(t)= 1, начальные условия для исходной системы определяются из следующих соотношений [2]:

                                 x0=0; x’0=0;...; x0 (n-k-2) =0;          

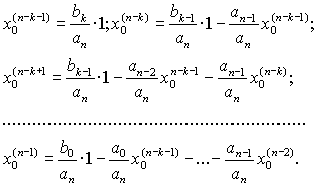                                                       (5)

Начальные условия для аппроксимирующего уравнения (2) определяются из приведенной системы уравнений при соответствующей замене коэффициентов полинома дифференциального уравнения. Коэффициенты числителя аппроксимирующей передаточной функции -di  определяются после приравнивания начальных условий и решения полученной системы уравнений:

                                  x0 (n-k-1)  = x10 (m-l-1) ,

                                   x0 (n-k-)  = x10 (m-l-) ,                     

                                  x0 (n-k+1)  = x10 (m-l-1) ,  

                                  …………………. ,                                                  (6)

                                  x0 (n-1)  = x10 (m-1) ,

Коэффициенты полинома знаменателя этой функции Сi определяются из равенства соответствующих интегральных оценок на основании уравнений (1), (3). Точность аппроксимации определяется формулой [1, 3]:

                                ;  

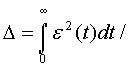
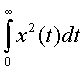 где: e (p)=1/p[W(p) - W1(p)].

Вычисление интегралов 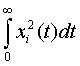 проводится с помощью почленного интегрирования по частям и решения системы уравнений, образованной при умножении исходного уравнения (2) поочередно на  x(n-1) , x(n-2) , ..., x:

                          

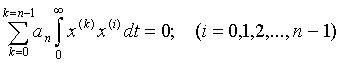
2

 

и при умножении на x(m-1); x(m-2);...; x аппроксимирующего уравнения (4):

                          

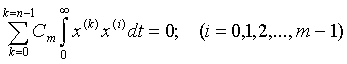
В дальнейшем воспользуемся следующими символами,  определяющими интегралы квадратичных оценок:

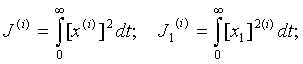
Для исследуемого уравнения с передаточной функцией (3) начальные условия, определяемые по (6) будут следующими:

                               ,                              (7)

а для уравнения пониженного порядка (3.23): 

                                       .                                           (8)

На основании (6) определяем коэффициенты числителя аппроксимирующего уравнения: .

Коэффициенты знаменателя этого уравнения определяются из (1) путем приравнивания интегралов         

                                         .                                                  (9)

 Для исследуемого уравнения табличные интегралы будут иметь следующие значения:

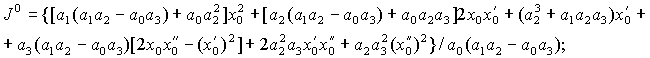
Для уравнения второго порядка:

                                                    

Подставив соответствующие значения начальных условий (7) и (8), на основании (3.63) получим систему уравнений

                  

   3

                                                                                           

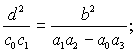
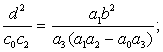
решение которой при а0 = с0 =1  дает значения  коэффициентов  уравнения второго порядка:

                           с1 = (a1a2 - a0a3)/a12;  c2 = a3/a1 ;  d = b/a1;                       (10)

 И аппроксимирующая передаточная функция будет иметь вид:

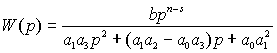                            ;                              (11)

   При таком методе  в аппроксимирующих уравнениях (4) учтены весовые значения коэффициентов всех производных исходных уравнений, что повышает точность аппроксимации.

Автоматизированное исследование метода с использованием программы AlgEq exe показало – для конкретных динамических систем отклонения АЧХ составляет не более 2 %, что определяет возможность применения данного метода при синтезе и анализе динамических систем. При этом упрощается и сокращается процесс автоматизированного моделирования динамических систем, особенно при спектральном анализе параметрических воздействий, с использование комплексных программ, таких как Classic, Electronics Workbench, АДАПЛАБ, Math Lab,  и т.д.

 

Литература.

1. Желонкин А.И. Инвариантный метод исследования динамических систем // Приборы и системы: – 2004. №6. – С. 23 – 27.

2. Желонкин А.И.   Инвариантное моделирование динамических процессов и систем // Естественные и технические науки. – 2008. № 4. – С. 28–31. 

3. Петров Б.Н и др. Принцип инвариантности в измерительной технике. – М.: Наука. – 1976. – 214 с.

 

 

 

 

 

4