ПСЕВДОПЕРИОДИЧЕСКИЕ
РЕШЕНИЯ НЕЛИНЕЙНЫХ СИСТЕМ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПЕРЕМЕННЫМИ
КОЭФФИЦИЕНТАМИ
Алеуова З.Ж., Арыстанова А.Б.
Западно-Казахстанский
государственный университет имени
М. Утемисова
Рассмотрим нелинейную систему
дифференциальных уравнений в виде
![]() ,
(1)
,
(1)
где ![]() вектор-параметр,
вектор-параметр, ![]() вектор,
вектор, ![]() матрица,
матрица, ![]() вектор-функция, которые обладают свойством непрерывности и
периодичности по
вектор-функция, которые обладают свойством непрерывности и
периодичности по ![]() с периодом
с периодом ![]() , такие что:
, такие что:
![]() (2)
(2)
![]() (3)
(3)
и функция ![]() удовлетворяет условию
Липшица по
удовлетворяет условию
Липшица по ![]() с константой
с константой ![]()
![]() (4)
(4)
Из условия (4)
следует, что
![]() (5) где
(5) где ![]() ,
, ![]() рационально несоизмеримые положительные постоянные,
рационально несоизмеримые положительные постоянные, ![]() множество
целочисленных векторов.
множество
целочисленных векторов.
Функция ![]() называется
псевдопериодической [1], если она
периодическая по
называется
псевдопериодической [1], если она
периодическая по ![]() с периодом
с периодом ![]() , которая при
, которая при ![]() обращается в
квазипериодическую функцию с частотным базисом
обращается в
квазипериодическую функцию с частотным базисом ![]() .
.
Пусть ![]() решение системы (1), с начальным условием
решение системы (1), с начальным условием
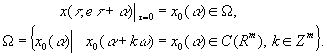 (6)
(6)
Очевидно, что всякое ![]() - псевдопериодическое решение
- псевдопериодическое решение ![]() при
при ![]() имеет начальную
функцию из класса
имеет начальную
функцию из класса ![]() .
.
Поставим
задачу об исследовании вопроса о существовании псевдопериодических решений системы
(1) при условиях (2) и (3).
Для решения
этой задачи нам достаточно ограничиться решениями системы (1) с начальными
функциями, удовлетворяющими условию (6).
Предположим, что соответствующая системе
(1) линейная однородная система не имеет псевдопериодических решений кроме
нулевого.
Тогда можно показать для ее матрицанта ![]() условие
условие
![]() (7)
(7)
Теперь для того, чтобы установить существование и
единственность псевдопериодического решения нелинейной системы (1) будем
распространять метод исследования псевдопериодических решений [2], линейной
системы дифференциальных уравнений
![]() , (8)
, (8)
на случай нелинейной системы (1), где ![]() непрерывная
непрерывная ![]() –псевдопериодическая
–псевдопериодическая ![]() вектор-функция.
вектор-функция.
Единственное псевдопериодическое решение
системы (8) в работе [2] представлено в виде
![]() (9)
(9)
где
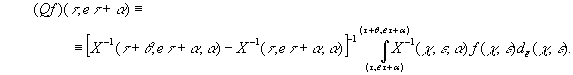 (10)
(10)
Решение (9) принадлежит к пространству ![]()
![]() периодических непрерывных
при
периодических непрерывных
при ![]() нормой
нормой ![]()
![]() вектор-функций
вектор-функций ![]() . В этом пространстве ограничен оператор
. В этом пространстве ограничен оператор ![]() , причем переводит полное пространство
, причем переводит полное пространство ![]() в себя и
в себя и
![]()
Действительно, что этот оператор класс ![]() непрерывных
непрерывных ![]() вектор-функций
вектор-функций ![]() переводит в себя:
переводит в себя:
![]() . (11)
. (11)
На основе
того, что ![]() , при условии (6), легко будем иметь
, при условии (6), легко будем иметь
![]() . (12)
. (12)
Из этих двух
свойств (11) и (12) следует, что оператор ![]() пространство
пространство ![]() непрерывных псевдопериодических по
непрерывных псевдопериодических по ![]() с периодом
с периодом ![]()
![]() вектор-функций переводит в себя:
вектор-функций переводит в себя:
![]() (13)
(13)
Так как
оператор ![]() действует на
вектор-функцию поточечно, непрерывно и периодично, то он ограничен.
Следовательно, для всех
действует на
вектор-функцию поточечно, непрерывно и периодично, то он ограничен.
Следовательно, для всех ![]() имеем
имеем
![]() (14)
(14)
где ![]()
Таким
образом, псевдопериодическое решение (9) системы (8) при помощи оператора ![]() представили в виде
представили в виде ![]() причем в силу (14)
имеем оценку
причем в силу (14)
имеем оценку
![]() (15)
(15)
Теперь на
основе вышеприведенного рассмотрим нелинейный оператор ![]() определенный в шаре
определенный в шаре ![]()
![]() пространства
пространства ![]() вектор-функций
вектор-функций ![]() , определенный в виде
, определенный в виде
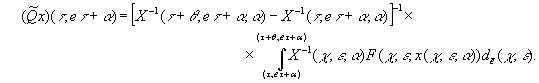 (16)
(16)
Далее, для установления существования единственного
псевдопериодического решения нелинейной системы (1) необходимо показать, что
оператор ![]() переводит шар
переводит шар ![]() в себя и является сжимающимся.
в себя и является сжимающимся.
Оценим соотношение (16) при условии (5) с учетом ![]() и оценки (14):
и оценки (14):
![]() .
.
Следовательно, при условиях (3) и
![]() (17)
(17)
с учетом свойства (13) оператора ![]() убеждаемся, что
оператор
убеждаемся, что
оператор ![]() переводит шар
переводит шар ![]() в себя, причем в силу условия (4) имеем
в себя, причем в силу условия (4) имеем
![]()
![]() . (18)
. (18)
Так как ![]() , то из условия (17) следует, что
, то из условия (17) следует, что ![]() . Тогда из (18) имеем сжатость оператора
. Тогда из (18) имеем сжатость оператора ![]() .
.
Следовательно,
по принципу неподвижных точек [3,4] оператор ![]() в шаре
в шаре ![]() имеет единственную
неподвижную точку
имеет единственную
неподвижную точку
![]()
Таким
образом, имеет место следующее утверждение.
Теорема 1. Пусть
выполнены условия (2)-(4), (7) и (17). Тогда нелинейная система (1) имеет
единственное псевдопериодическое решение с периодом ![]() .
.
В
заключение рассмотрим квазипериодическую по ![]() систему
дифференциальных уравнений
систему
дифференциальных уравнений
![]() , (19)
, (19)
полученную из системы (1) при ![]() .
.
Теорема
2. При условиях теоремы 1 квазипериодическая по ![]() с частотным базисом
с частотным базисом ![]() нелинейная система (19) имеет единственное квазипериодическое
решение
нелинейная система (19) имеет единственное квазипериодическое
решение ![]() с тем же частотным
базисом.
с тем же частотным
базисом.
Действительно,
теорема 2 является следствием теоремы 1 при значении ![]() .
.
В данной работе использованы некоторые
идеи методов работ [5,6] и обобщены результаты заметки [7] на случай
псевдопериодических коэффициентов квазилинейных систем.
СПИСОК ИСПОЛЬЗОВАННОЙ
ЛИТЕРАТУРЫ
1.
Urabe M. Green
functions of pseudoperiodic differential operators
// Lect. Notes. Math. 1971. - Р.106-122.
2.
Алеуова З.Ж.
Псевдопериодические решения линейных дифференциальных уравнений с переменными
коэффициентами // III Ержановские чтения, 2010 г. (в
печати)
3.
Демидович Б.П., Лекции
по математической теории устойчивости. - Москва: Наука, 1967. – 472 с.
4.
Петровский И.Г. Лекции
по теории обыкновенных дифференциальных уравнений. – Москва: Изд-во МГУ, 1984.
– 296 с.
5.
Умбетжанов Д.У., Почти
многопериодические решения дифференциальных уравненений в частных
производных. - Алма-Ата: Наука, 1979. - 211 с.
6.
Сартабанов Ж.А.,
Кульжумиева А.А., Периодические по многомерному времени решения систем
уравнений с оператором дифференцирования по направлению векторного поля на торе
// Евразийский математический журнал. - 2007. - №1. – С. 62-72.
7.
Сартабанов Ж.А., Алеуова
З.Ж. Псевдопериодические решения нелинейных систем дифференциальных уравнений с
постоянными коэффициентами // Вестник КазНПУ. – Алматы, 2008. №2(18).