Технические науки /12. Автоматизированные системы управления на производстве

К.э.н. Сизиков А.П.

Самарский государственный экономический университет, Россия

АЛГОРИТМ ОПТИМИЗАЦИИ ДВУХУРОВНЕВОЙ ПРОИЗВОДСТВЕННОЙ СИСТЕМЫ

Рассматривается двухуровневая модель некоторой системы. Первый (верхний) уровень представлен линейной моделью с переменными параметрами. Это, если речь идет о производственно-технологических объектах, как правило, модель «затраты - выпуск» и/или представленная в матричном виде сетевая потоковая модель. Соответственно, переменные имеют смысл интенсивностей «технологий» и/или материальных потоков. К этим переменным можно с помощью соответствующих коэффициентов (в общем случае переменных) привязать любые производственные факторы и, соответственно, сформулировать целевую функцию всей системы. Для удобства дальнейшего изложения запишем модель верхнего уровня в обобщенной канонической форме:

. (1)

Вычислительная схема строится с использованием метода генерирования столбцов [1]. Столбцы генерируются в результате решения локальных задач (задач второго уровня). Модель центра играет роль координатора локальных решений. Эту функцию она осуществляет путем расчета симплексных мультипликаторов, которые трактуются в данном случае как «цены» ингредиентов (ресурсов, продуктов) системы. Каждая локальная модель с учетом этой информации оптимизирует собственную «технологию» и соответственно коэффициенты представляющего ее столбца «затраты - выпуск» и передает их в базовую модель.

Каждый столбец модели верхнего уровня является представителем (агрегатом) модели соответствующего элемента, или, иначе говоря, вектор-столбцом , , где - множество возможных «технологий» узла. Решение обобщенной задачи сводится к формированию оптимального базиса путем генерирования столбцов, являющихся крайними точками допустимых множеств технологий.

Алгоритм:

1. Формируем начальный вариант задачи, включая в матрицу условий по одному представителю множеств , . Находим условно-оптимальный базис и соответствующую ему обратную матрицу.

2. Вычисляем соответствующие текущему базису симплексные мультипликаторы , где - базисная матрица, - коэффициенты целевой функции при базисных столбцах.

3. Генерируем столбцы с минимальными оценками замещения, т.е. находим решения локальных задач

, . (2)

4. Проверяем условие . Если оно выполняется, то текущий базис оптимален, решение получено. В противном случае переходим в следующий пункт.

5. Вводим в базис столбец . Формируем новую матрицу . Столбец, выводимый из базиса, удаляем из задачи. Переходим в п. 2.

Эту вычислительную схему можно проиллюстрировать на примере оптимизации системы, состоящей из взаимосвязанных производств. Согласно Леонтьеву для нее можно записать уравнения материального баланса:

, (3)

где - матрица коэффициентов прямых материальных затрат; - вектор валового продукта; - вектор конечного продукта.

Следуя неоклассической теории, будем полагать, что -й производственный объект описан степенной производственной функцией:

, (4)

где - масштабный множитель; - коэффициент затрат труда; - коэффициент затрат -го продукта; - соответствующий коэффициент эластичности, , , .

Деля обе части (4) на , получаем:

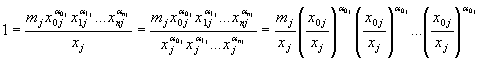. (5)

Таким образом, из (5) следует, что в балансовой модели -й объект может быть представлен столбцом параметры, которого принадлежат множеству решений по уравнения

. (6)

где , - коэффициент прямых затрат -го продукта .

Сформулируем следующую задачу: найти вектор валового производства, при котором заданный конечный продукт обеспечивается с минимальными затратами труда. Математически это можно записать так:

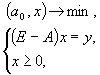(7)

где

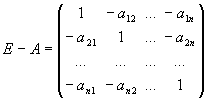. (8)

Согласно описанному выше алгоритму, на каждом шаге нужно генерировать столбцы матрицы , решая задачи

. (9)

где , .

Функция Лагранжа:

. (10)

Условия стационарности:

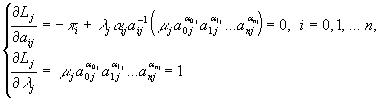
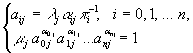
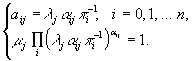
Решение:

. (11)

Далее идет цикл: 1) расчет мультипликаторов по формуле и 2) расчет технологических коэффициентов по формуле (11). И так до получения приемлемого по точности результата. Расчеты показывают, что процесс монотонно сходится за число итераций, соизмеримое с размерностью задачи.

Алгоритм по сути дела моделирует рыночный механизм. Каждая производственная система, используя эффект взаимозаменяемости ресурсов и симплексные мультипликаторы, играющие роль цен, оптимизирует свою технологию по критерию собственной прибыли, а в результате достигается цель всей системы.

Литература:

1. Лэсдон Л. Оптимизация больших систем. Главная редакция физико-математической литературы изд-ва «Наука», М., 1975.