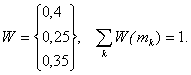Економіка / 10. Економіка підприємства

Гордєєва Т.А.

Хмельницький національний університет

ФОРМУВАННЯ АСОРТИМЕНТУ ПРОДУКЦІЇ ДЛЯ ПІДПРИЄМСТВ МАШИНОБУДІВНОГО КОМПЛЕКСУ НА ОСНОВІ ТЕОРІЇ НЕЧІТКИХ МНОЖИН

Нові інформаційні та виробничі технології зумовлюють радикальні зміни практично всіх аспектів діяльності промислового підприємства. Акцент ставиться на скорочення періоду розробки продукту та доставки його до споживача. В умовах оновлення обладнання, електронного зв’язку та скорочення виробничих циклів потрібно переходити до формування перспективного асортименту продукції на основі потреб та вподобань споживачів.

Актуальним завданням менеджменту є встановлення балансу між стратегічними і оперативними рішеннями. Сучасні умови діяльності підприємств такі, що не дають можливості для існування тривалого періоду адаптації, тому підприємство повинне трансформуватися в організацію, здатну приймати швидко і обґрунтовано як оперативні, так і стратегічні рішення.

Для будь-якого підприємства розробка перспективного асортименту –завдання стратегічне. Його суть полягає в тому, щоб сформувати номенклатуру та структуру продукції, що приносить виробнику прибуток, та яка дозволить досягти поставлених цілей і забезпечити стійке функціонування підприємства у майбутньому. Віднаходження перспективного асортименту гарантує підприємству формування «ядра» продукції, яке буде реалізоване на ринку з мінімальним ризиком для виробника. Для вирішення завдання необхідна дослідницька робота, в процесі якої відбувається збір інформації про зовнішнє та внутрішнє середовище, про ринки, постачальників, споживачів, конкурентів, а також аналітична робота, мета якої – поступовий перехід до формування найбільш оптимальних пропорцій виробництва продукції.

При вирішенні задачі визначення асортименту в рамках деякої товарної групи точна статистична оцінка структури, як правило, ускладнена, особливо для підприємств машинобудування із багатономенклатурним виробництвом. Тому для вирішення даної задачі прийнятним, на нашу думку, може бути використання теорії нечітких множин. Основи теорії нечітких множин були закладені у роботах американського математика, професора Каліфорнійського університету (Берклі), Лотфі А. Заде [1].

Теорія нечітких множин дає схему вирішення проблем, в яких суб’єктивні судження відіграють істотну роль в оцінці фактора невизначеності. Завданням цієї теорії було побудувати функціональну відповідність між нечіткими лінгвістичними описами та спеціальними функціями, що виражають ступінь приналежності значень вимірюваних параметрів зазначеним нечітким описам. Згодом діапазон застосування теорії нечітких множин істотно розширився.

По суті постановка завдання полягає в наступному: підприємство машинобудівного комплексу, що випускає продукцію декількох типів, планує виробляти ряд найменувань продукції кожного типу та реалізовувати її заданому колу споживачів. Потрібно на основі інформації про попередню фінансово-господарську діяльність визначити перспективний асортимент: номенклатуру та структуру продукції, що буде виготовлятись. Дана продукція характеризуються набором певних ознак, за сукупністю яких один тип продукції має переваги над іншим, якщо його ознаки більш високо оцінюються певним споживачем.

Введемо позначення:

х_і – деякий i-й вид продукції, що випускається, i = 1,10;

Х = {х₁, ..., х₁₀} - множина продукції, що виробляється підприємством;

p_j – ознака товару, j = 1,6;

Р = {р₁, ..., p₆} – множина ознак продукції, що виробляється підприємством, а саме: ціна, можливий обсяг партії, функціональність, надійність, екологічність, естетичність;

m_k - споживач продукції підприємства, про якого є відомості щодо обсягів закупівель та видів продукції, якій надається перевага, k = 1, 3;

М = {m₁, ..., m_с} – множина споживачів продукції підприємства.

Для споживачів продукції на основі даних про результати їх співпраці з аналізованим підприємством визначається вагова функція:

За допомогою експертів – керівників та працівників відповідних структурних підрозділів підприємства – визначимо функцію приналежності нечіткої матриці R «Продукція-ознаки»: , що виражає відносний ступінь приналежності ознак продукції, що розглядається, та ступінь множини:

(1)

В нашому випадку дана матриця буде мати такий вигляд:

		p1	p2	p3	p4	p5	p6
	х1	1	0,9	0,6	1	0,7	0,8		5
	х2	0,4	0,9	0,4	0,7	0,3	0,4		3,1
	х3	0,4	0,6	0,3	0,7	0,4	0,4		2,8
R=	х4	0,4	1	1	0,9	0,6	0,5	S=	4,4	Sm=	5,1
	х5	1	0,7	0,7	0,6	0,6	0,9		4,5
	х6	1	0,7	0,6	0,7	0,5	0,9		4,4
	х7	1	0,6	0,6	0,7	0,7	1		4,6
	х8	0,6	1	1	0,9	0,7	0,6		4,8
	х9	0,7	0,7	0,8	0,8	0,7	0,6		4,3
	х10	1	1	0,7	0,7	0,7	1		5,1

Елементи рядків матриці R виражають відносні ступені притаманності ознак певним видам продукції: чим більш важлива ознака, тим вище значення функції. Аналогічно визначимо функцію приналежності , значення якої формують нечітку матрицю U «Продукція-споживачі».

		m1	m2	m3
	p1	1	1	0,7
	p2	0,9	0,7	0,8
U=	p3	0,9	0,8	0,9
	p4	0,8	1	0,5
	p5	0,7	0,8	0,9
	p6	0,7	1	0,8

Дана функція, яка також визначається за допомогою оцінок експертів, демонструє ступінь важливості ознаки p_j для відповідного споживача продукції m_k. Елементи рядків матриці U демонструють відносні ступені важливості ознак в момент прийняття рішення щодо придбання певного виду продукції певним споживачем.

Далі з елементів цих двох матриць будується нечітка матриця Т, елементи якої визначаються за допомогою операції композиції функцією приналежності:

(2)

для усіх

Елементи матриці Т характеризують ступінь сумісності відповідного виду продукції х_i з розглянутим споживачем продукції m_k.

		m1	m2	m3
	х1	0,82	0,88	0,73
	х2	0,51	0,53	0,45
	х3	0,46	0,49	0,40
T=	х4	0,72	0,74	0,66
	х5	0,74	0,79	0,68
	х6	0,73	0,78	0,65
	х7	0,75	0,82	0,69
	х8	0,79	0,82	0,72
	х9	0,71	0,74	0,64
	х10	0,84	0,89	0,77

Зрозуміло, що товари з низьким значенням функції не складуть економічного інтересу, тому вводиться поріг поділу, що дозволяє не купувати товари підвищеного ризику. Беручи до уваги вагову функцію та обираючи поріг поділу =0,324 , отримаємо підсумкову матрицю А, яка дозволяє визначити найкращу структуру асортименту виробництва продукції як за видами продукції, так і в розрізі споживачів продукції:

		m1	m2	m3
	х1	0,33	0,31	0,18
	х2	0,21	0,18	0,11
	х3	0,18	0,17	0,10
А=	х4	0,29	0,26	0,17
	х5	0,30	0,28	0,17
	х6	0,29	0,27	0,16
	х7	0,30	0,29	0,17
	х8	0,32	0,29	0,18
	х9	0,28	0,26	0,16
	х10	0,34	0,31	0,19

Сума елементів кожного рядка показує ступінь важливості товару х_i для виробника. Застосувавши сумування та нормування, отримаємо матрицю А₁, в якій перший стовпець відображає номенклатуру, а другий стовпець – структуру продукції, що випускається, для розглянутого нами підприємства:

		Sx	%
	х1	0,82	11,64
	х2	0,50	7,14
	х3	0,45	6,45
А1=	х4	0,71	10,14
	х5	0,74	10,55
	х6	0,73	10,32
	х7	0,76	10,76
	х8	0,78	11,11
	х9	0,70	9,99
	х10	0,84	11,90

Таким чином, на основі теорії нечітких множин визначено перспективний асортимент, що гарантує підприємству формування ядра продукції, яка буде реалізована споживачам на ринку із мінімально можливим ризиком. Маючи структуру асортименту, можна перейти до формування виробничого плану підприємства, який вже буде враховувати преференції споживачів.

Список використаної літератури:

1. Заде Л. Нечеткие множества и теория возможностей. Последние достижения: пер. с англ. / Под ред. Ягера P.P. - М.: Радио и связь, 1986. - 408 с.