Магістр 2 р.н., Присяга Т. А.

науковий керівник викладач Алексєєнко І. І.

ХНЕУ, Україна

Оптимізація процесу прогнозування прибутку підприємств торговельної галузі

Актуальність теми. Функціонування підприємств на ринку України останнім часом пов’язане з низкою труднощів, а саме: змінюються організаційні форми підприємств різних галузей, ускладнюються економічні та соціальні зв’язки й відносини. Тож у діяльності менеджерів акцент доводиться робити не на стандартні рішення, а на здатність досить оперативно реагувати на зміни, що відбуваються у мікро- та макросередовищі.

Управління структурою капіталу торговельних підприємств має за мету створення цільової структури капіталу, яка б дозволила успішно реалізувати фінансову стратегію компанії в цілому. Оптимізація структури капіталу неможлива без попередньої оцінки вже існуючої структури та прогнозування майбутнього стану, що дасть ймовірний варіант розвитку підприємства, та дасть відповіді на питання, в якому обсязі та який капітал треба використовувати в заданих умовах, щоб досягти бажаних цілей [5].

Аналіз наукових досліджень. Багато вчених, серед яких А. Н. Іванов, Г. Д. Ковальова, А. Н. Колмагоров, А. Я. Хінчин, І. Г. Журбенко, Ю. П. Лукашин, Е. Є. Тихонов, брали участь у розвитку математичного апарату і його застосуванні в дослідженні і прогнозуванні часових рядів, та отримали важливі наукові результати. Але прогнозування саме елементів фінансової звітності, а саме, пасиву балансу потребує більш детального розгляду.

Метою статті є обґрунтування доцільності використання адитивної моделі прогнозування прибутку підприємств, з урахуванням особливостей функціонуючих підприємств торговельної галузі задля забезпечення ефективного управління структурою їх капіталу.

Виклад основного матеріалу. З метою прийняття раціональних управлінських рішень стосовно стратегічного управління підприємством, а саме, управління структурою капіталу та її оптимізацією, будується адитивна модель для величин прибутку підприємств як основного джерела формування капіталу функціонуючого підприємства. Загальний вигляд адитивної моделі наступний:

Y = TСt+ S + E , (1) [3]

де TСt – тренд-циклічна компонента;

S – сезонна компонента;

E – випадкова компонента або помилка.

Ця модель передбачає, що кожен рівень тимчасового ряду може бути представлений як сума трендової, сезонної і випадкової компонент [4, c. 56]. Тренд і циклічну компоненту зазвичай об’єднують в одну тренд-циклічну компоненту (TtCt). Різниця між циклічною і сезонною компонентою полягає в тому, що остання має регулярну (сезонну) періодичність, тоді як циклічні фактори звичайно мають більш тривалий ефект, який, до того ж, міняється від циклу до циклу. У нашому випадку циклічні коливання носять сезонний характер, оскільки особливістю торговельного підприємства є наявність сезонної складової [5].

При наявності великих масивів даних за тривалі проміжки часу можна виявити циклічні коливання, пов’язані із загальною динамікою кон’юнктури ринку. Враховуючи все вищесказане, немає сенсу розраховувати циклічну компоненту для ТОВ «Дорожня Карта» за даний проміжок часу.

Для наочнішого уявлення щодо послідовності побудови адитивної моделі було побудовано схему, яка відповідає заданій проблематиці (рис. 1).

Особливістю другого етапу є використаня розрахованої оцінки для розрахунку значень сезонної компоненти S. Для чого знайдемо середні за кожний квартал по всім рокам оцінки сезонної компоненти Si.

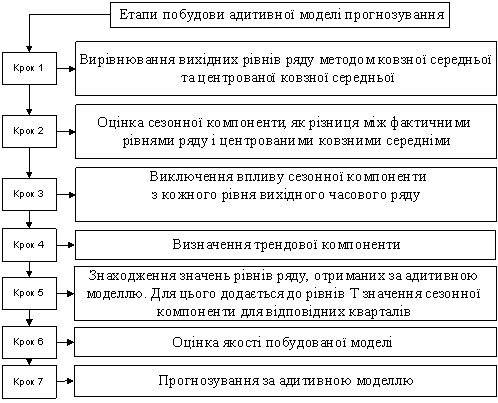
Рис. 1. Етапи побудови адитивної моделі [5]

У моделях із сезонною компонентою зазвичай передбачається, що сезонні впливи за період взаїмокомпенсуються [1]. В адитивній моделі це виражається в тому, що сума значень сезонної компоненти по всіх кварталах повинна дорівнювати нулю.

Для розрахунку скоригованої сезонної компоненти моделі маємо розрахувати суму середньої оцінки сезонної компоненти за чотири квартали та коригуючий коефіцієнт, який розраховується як поділ розрахованої суми на кількість кварталів [5]. Розраховуємо скориговані значення сезонної компоненти за формулою:

Siск = Si – k , (2) [3]

де Siск – скоригована сезонна компонента;

Si – середня оцінка сезонної компоненти;

k – коригуючий коефіцієнт.

Правильність розрахованих значень перевіряемо на рівність нулю суми значень сезонної компоненти. У нашому випадку, сума дорівнює нулю, тож головне правило побудови адитивної моделі виконано.

Для впровадження четвертого кроку проведемо аналітичне вирівнювання ряду (T + E) за допомогою лінійного тренду за формулою (3):
 
y = a + b*t, (3) [6, c. 85Ошибка! Источник ссылки не найден.]
 
де a – початковий рівень часового ряду в момент часу t = 0;
b – середній за період абсолютний приріст рівней ряду.
 
 Результати аналітичного вирівнювання наступні: Т = 11018 + 8,2797* t.
Підставляючи в це рівняння значення t = 1,2, ..., 18, знайдемо рівні T для кожного моменту часу.

Апробацію щодо доцільності використання запропонованої адитивної моделі здійснено за даними фінансової звітності ТОВ «Дорожня Карта» за період 2008 – 2012 роки (табл. 1).

Таблиця 1

Квартальні значення нерозподіленого прибутку ТОВ «Дорожня Карта»

	2008 р.	2009 р.	2010 р.	2011 р.	2012 р.
1 кв	9505,2	11087	11090	11092	11108
2 кв	11545,8	11080	11092	11094	11109
3 кв	12194	11087	11098	11100	прогноз
4 кв	11075	11088	11090	11102	-
Сума	44320	44342	44370	44388	22217

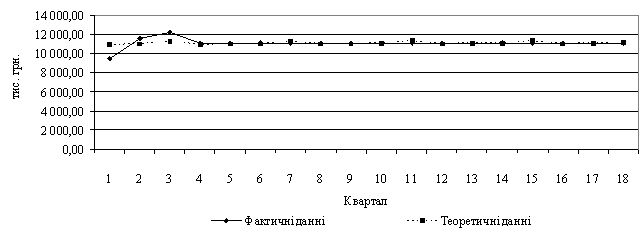
На одному графіку відкладемо фактичні значення рівнів часового ряду і теоретичні, отримані за адитивною моделлю (рис. 2).

Рис. 2. Відповідність фактичних і теоретичних значень адитивної моделі статі «Нерозподілений прибуток»
 
 Для оцінки якості побудованої моделі за кроком 6, застосуємо суму квадратів отриманих абсолютних помилок. 
 
R2 = 1 - ∑E2 / ∑((yt – ycp)2)     (4) [5]
 
За формулою 4 отримали значення суми квадратів, яке дорівнює 0,11. Отже, можна сказати, що адитивна модель пояснює 89% загальної варіації рівнів часового ряду значень нерозподіленого прибутку по кварталах за 4 роки.
 Останнім етапом є прогнозування за адитивною моделлю. Зробимо прогноз величини нерозподіленого прибутку на III квартал 2012 року. Прогнозне значення Ft рівня часового ряду в адитивної моделі є сума трендової та сезонної компонент [1]. 
Аналогічним чином, можна будувати прогнозні значення за складовими пасиву балансу. Отриманий результат розрахованого значення та прогнозу зведено до табл. 2.
 Одразу розрахуємо похибку отриманих теоретичних значень за адитивною моделлю, що дозволить говорити про адекватність отриманої, бо похибка становить 1,41%. 

Таблиця 2

Результати прогнозування величини нерозподіленого прибутку підприємства

Елемент прогнозування	Прогноз 3 кв. 2012	Фактичні данні	Похибка
Нерозподілений прибуток	11 381,93	11222	1,41%

Побудована адитивна модель, з урахуванням сезонності та тренду, є адекватною, бо пояснює 89% загальної варіації рівнів часового ряду значень нерозподіленого прибутку, тому її можна застосовувати для прогнозу інших елементів пасиву балансу, які мають поступову тенденцію росту або спаду.

Отже, оптимізація структури капіталу неможлива без попереднього прогнозу її значення, що забезпечує необхідний попередній контроль за утворенням і використанням фінансових ресурсів підприємства, створює умови зміцнення фінансового стану підприємства, дозволяє покращити результати фінансово-господарської діяльності підприємства.

Не треба забувати про нестабільність зовнішнього середовища, динаміку зміни характеристик капіталу під впливом різноманітних ендогенних та екзогенних чинників, що викликають аритмію в русі фінансово-матеріальних потоків, що приводить до дисбалансу структури капіталу, зниження фінансової стійкості.

Тому надзвичайно актуальним є розробка та впровадження таких методів прогнозування, які б забезпечили можливість довгострокового планування його діяльності, задля зміцнення фінансової стабільності розвитку підприємства, швидке реагування на зміни структурних елементів, що дозволить приймати обґрунтуванні рішення щодо позиціонування підприємства на ринку у довго – та короткостроковій перспективі.

Література:

1. Иванов А. Н. Построение эконометрических моделей и прогнозирование в MS Excel : сборник лабораторных работ [Электронный ресурс] / А. Н. Иванов. – Режим доступа : http://edu.dvgups.ru/metdoc/enf/prmatem/ ekonometrika/metod/lab_excel/ivanov_1.htm

2. Ковалева Г. Д. Применение теории временных рядов в экономических исследованиях : Курс лекций / Новосибирск : Издательство НГУ, 2008. – 56 с.

3. Компоненты и сезонная декомпозиция временного ряда [Электронный ресурс]. – Режим доступа : http://helpstat.ru/2012/03/komponentyi-i-sezonnaya-dekompozitsiya-vremennogo-ryada/

4. Лукашин Ю. П. Адаптивные методы краткосрочного прогнозирования временных рядов: учеб. Пособие / Ю. П. Лукашин. – М. : Финансы и статистика, 2003. – 416 с.

5. Прогнозирование. Модели временных рядов [Электронный ресурс]. – Режим доступа : http://proasy.narod.ru/All/LK/9_Prognozirovanie_Modeli_ vremennyx_ rjadov

6. Тихонов Э. Е. Методы прогнозирования в условиях рынка: учебное пособие / Э. Е. Тихонов. – Невинномысск, 2006. – 221 с.