УДК
004.922
Романюк А.Н., Поддубецкая М.П., Малёваный В. Г.
Винницкий национальный технический университет
ВЫСОКОПРОИЗВОДИТЕЛЬНЫЕ МЕТОДЫ ПОВОРОТА ОКНА ИЗОБРАЖЕНИЯ НА ЗАДАННЫЙ УГОЛ
В данной
работе разработан метод реализации процедуры поворота окна изображения на заданный
угол. Метод не содержит синусно-косинусные преобразования, что значительно повышает
качество процедуры формирования графических динамических сцен.
Ключевые
слова: метод поворота окна изображения на заданный угол, метод формирования
окна под произвольным углом к координатным
осям.
In this article a method of
implementing the procedure of rotation of the image window to the specified angle is developed. The
method does not include the sine-cosine
transform, which greatly improves the
quality of the procedure of forming dynamic graphic scenes.
Введение
Компьютерная графика позволяет существенно увеличить
пропускную
способность информационного канала, через который осуществляется двусторонняя связь пользователя и компьютера, в
связи с чем роль и значение графического изображения и результатов вычислений в
промышленности и научно-исследовательской практике непрерывно растет. На современном этапе развития
трехмерной графики остро ставится вопрос о формировании динамических
графических изображений в реальном времени и в интерактивном режиме, когда
предполагается, что траектории движения объектов не заданы заранее, а
определяются действиями пользователя в процессе взаимодействия с системой. Для
таких режимов предъявляются жесткие требования к времени формирования
трехмерных графических сцен.
При формировании динамических изображений
широко используется поворот окон изображений на заданный угол, что предполагает
необходимость разработки методов повышения качества этой трудоемкой процедуры.
Анализ
методов и постановка задачи
В средствах компьютерной графики наибольшее распространение
получил метод поворота, в котором используется синусно-косинусное
преобразование [1,2].
На рис.1 изображены геометрические соотношения между
начальной системой 0XY и системой 0X1Y1, которую получили при повороте начальной системы на угол
a.
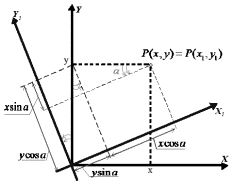
Рис. 1. Поворот системы
координат
![]()
С
помощью соотношений на рис.1 получаем систему уравнений:
 X1 = Xcosa + Ysina,
X1 = Xcosa + Ysina,
Y1 = Ycosa – Xsina,
что можно представить в матричном виде:
![]() .
.
Недостаток метода состоит в высокой трудоемкости,
поскольку синусно-косинусные преобразования выполняются для каждой точки
изображения. В связи с этим возникает необходимость разработки более простых
методов поворота изображения.
Метод «цифра за цифрой» - итерационный метод сведения прямых вычислений сложных функций к
выполнению простых операций сложения и сдвига. Отличительной особенностью CORDIC методов является их хорошая аппаратная
реализация и сравнительная простота. Последние работы показали, что необходимый
результат при вращении точки можно получить за ограниченное и заранее
определенное время работы CORDIC архитектуры – максимум за 15 тактов её работы.
Однако
даже использование таких средств является не всегда эффективным. Например, в
полиграфических системах, где возникает потребность в обработке больших
растровых изображений, системах распознавания текста, системах для нанесения
текстур. При повороте растровых изображений кроме проблемы больших объемов
вычислений существует так же проблема искажения исходного изображения,
накладывающая свои ограничения на построение графических систем [3,4].
Разработка
методов поворота окна изображения на заданный угол
Сущность метода состоит в следующем. Декартова плоскость 1 и соответствующая ей система
координат ХОY образованна плоскостью экрана индикатора изображения, а декартова
плоскость 2 и соответствующая ей система
координат Х1О1Y1 – плоскостью матрицы
светочувствительных элементов (рис.2).
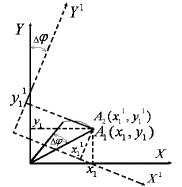
Рис. 2. Функциональный метод поворота
![]()
В начальный момент времени точка А1 с координатами Х1, Y1 отображается на экране
индикатора. Матрица светочувствительных элементов, которая повернута по
отношению к экрану на угол jD, воспринимает точку в системе
координат Х1О1Y1, по отношению к которой
последняя имеет координаты Х11,
Y11. Очевидно,
что отображая на экране точку с координатами Х11, Y11, осуществляется поворот исходной
точки на угол Dj в системе координат ХОY. Выполняя указанную процедуру
для всех точек изображения, за время одного кадра осуществляется поворот
изображения на угол Dj.
За счет повторения процесса n раз, где n=j/jD, обеспечивается поворот
изображения на заданный угол j. Поскольку исходная и новая
системы координат есть прямоугольными декартовыми с одинаковыми единичными
отрезками по осям, то при преобразовании сохраняются все метрические свойства
геометрических фигур.
Недостаток функционального метода поворота состоит в
относительно большой погрешности преобразования.
Предлагается метод формирования окна под
произвольным углом к координатным осям.
Векторы АВ и АС (рис. 3) имеют одинаковые углы
наклона соответственно к осям абсцисс и ординат. Таким образом, их составляющие
шаговые приращения относительно заданных координатных осей совпадают и
отличаются только знаками. Таким образом, при формировании выходного вектора АВ путем запоминания его шаговых
приращений можно реализовать направляющую АС.
Для этого при формировании i-той строки в направлении АВ запоминают тип i-го шагового
приращения и формируют его после завершения отработки заданного вектора в
другом ортогональном направлении.
Для растеризации
прямоугольного окна изображения производится шлейфовый обход точек прямоугольного окна изображения. При
шлейфовому обходе производится считывание точек
изображения, расположенных в первой строке АВ
окна изображения (рис. 4), после чего формируют функцию перехода от точки В к точке С на одну дискрету. После выполнения указанных действий направление обхода
меняется на противоположный, т.е. обход проводится вдоль вектора СД, знаки которого противоположные по
отношению к вектору АВ. Аналогичная
процедура обхода имеет место для всех последующих строк окна.
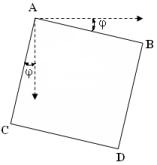
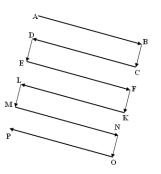
Рис. 3. Размещение окна относительно осей координат Рис. 4.
Шлейфовый
обход строк
окна


Пусть необходимо растрировать прямоугольное
окно ABQP (рис. 5), внутренние точки
которого определяют некоторое текстурное
изображение.Для этого
выполняют следующие действия. Определяют приращение D Х, D Y базового
вектора АВ. С
использованием функции линейной интерполяции определяют потактно координаты
точек изображения в направлении базового вектора АВ. При достижении точки В,
что соответствует конечной точке вектора АВ,
формируют сигнал перехода от точки В
к точке С. Для этого при формировании
шаговой траектории базового вектора АВ
запоминают значение шагового приращения, что
соответствует точке 1 вектора АВ, и
при достижении точки В формируют
шаговое приращение с противоположным знаком по оси абсцисс и заменой
ортогональных составляющих местами. Таким образом будет обеспечено переход в
точку С, размещенную от точки В на одну дискрету. В дальнейшем изменяют направление базового вектора
на противоположный и повторяют вышеперечисленные действия. Так при формировании
вектора CD запоминают шаговое
приращение, формирующейся во втором интерполяционном такте. Зафиксированный шаговое приращение используют в точке D
для перехода в точку E. Аналогично,
при формировании третьего вектора запоминают значение шагового приращения в третьем такте, который используют в точке F для перехода в точку К.
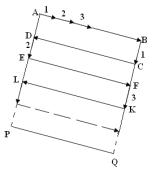
Рис. 5. Определение кординатних перемещений для боковых сторон окна
В общем случае при формировании i-той строки запоминают тип i-го шагового приращения и
формируют его относительно оси ординат после завершения отработки заданного
вектора. Описанные действия повторяют до момента окончания поворота окна
изображения.
Предложенный метод растеризации прямоугольного окна, сформированного
под некоторым углом к координатным осям, имеет простую аппаратную реализацию и предполагает
использование не двух, а только одного линейного интерполятора, что позволяет
до двух раз уменьшить аппаратные затраты.
Устройство для поворота (рис.
6) содержит цифровой интерполятор 1, счетчики 2, 3, 13, 14, Д-триггеры 4, 6, 9,
11, блок сравнения 5, счетный триггер 7, элемент I 8, логический преобразователь 10, элемент ИЛИ 12,
блок ввода 15.
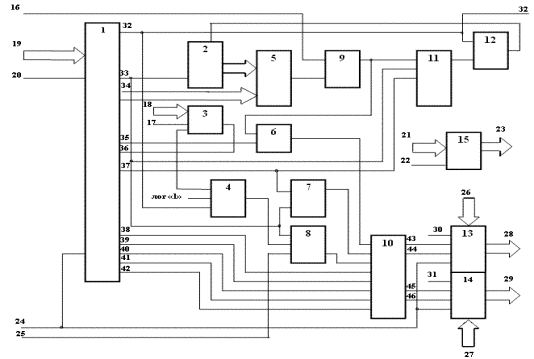
Рис. 6. Структурная
схема устройства для формирования окна изображения под заданным углом к координатным осям
В координатные счетчики 13 и 14 заносятся, соответственно, абсцисса и
ордината первой точки первой строки окна, а в счетчик 3 - количество строк
исходного окна. Значение приращений координат базового вектора и их знаки
запоминаются в интерполяторе 1. Указанные действия являются подготовительными.
В дальнейшем в каждом такте определяются координаты точки окна, по
которым в видеопамять записываются данные от блока ввода 15.
Счетчик 2 подсчитывает количество сформированных строк в прямоугольном
окне изображения. Схема сравнения 5 и триггер 9 определяют момент времени для
запоминания шагового приращения, который используют как функцию перехода от
одной строки окна изображения к другой. Это имеет место при формировании i-го
шагового приращения в i-й
строке. Д-триггер 6 используется для запоминания значения шагового приращения,
который применяется после окончания воспроизведения вектора как функцию
перехода от текущей строки окна изображения к следующей. Для шлейфового обхода
строк окна счетный триггер 7 формирует
признак четности строк.
Логический преобразователь формирует сигналы изменения состояний координатных счетчиков.
После формирования текущей строки окна состояние счетчика 3 уменьшается на единицу. При достижении счетчиком 3 нулевого состояния процесс формирования окна изображения заканчивается.
Полученные при растеризации окна
изображения тексели усредняются по выбранному методу фильтрации.
Выводы
Предложенные в работе методы
реализации трудоемкой процедуры поворота окна изображения не содержат синусно-косинусные
преобразования, которые выполняются в классическом методе для каждой точки
изображения. Это позволяет существенно понизить время формирования
динамических графических сцен.
Список литературы
1. Цисарж В. В.
Математические методы компьтерной графики / В. В. Цисарж., Р. И. Марусин. — К.
: Факт, 2004. — 464 с.
2. Херн Д.,
Бейкер М. Компьютерная графика и стандарт OpenGL / Д. Херн, М. Бейкер. —
М. : Издательский дом "Вильямс", 2005. — 1168 с.
3. Байков В.Д.,
Смолов В.Б. Аппаратная реализация элементарных функций в ЦВМ / В. Д. Байков.,
В. Б. Смолов. — М. : Изд. ЛГУ, 1975. — 96 с.
4.
K. Maharatna, S. Banerjee, E. Grass, M. Krstic,
A. Troya. Modified virtually scaling-free adaptive CORDIC
rotator algorithm and architecture. / Maharatna K., Banerjee S., Grass E., Krstic M., Troya A. // IEEE
Trans. Circutes Syst. Video Technol., vol. 15, no. 11. — 2005.