Аменова С.М., Акишев Г.

Карагандинский государственный университет имени Е.А.Букетова, Казахстан

АБСОЛЮТНАЯ СХОДИМОСТЬ РЯДА ПО СИСТЕМЕ ФАБЕРА-ШАУДЕРА И БАНАХОВА АЛГЕБРА

Пусть - класс функций, определенных и непрерывных на отрезке с нормой .

Рассмотрим систему - Фабера-Шаудера ([1],С.214 ). Функции этой системы определяются следующим образом при ; функция при ; если же , то функция при , при и линейна на отрезках .

Пусть . Через обозначим класс всех функций , для которых , где - последовательность коэффициентов Фабера-Шаудера функции .

Если нормированная алгебра вдобавок полна, то она называется банаховой алгеброй (см.[2]).

Условия абсолютной сходимости рядов Фурье по тригонометрической системе суперпозиции функций исследовали Леви, Кацнельсон, Кахан, Марцинкевич, Ривьер (см.[3]).

Для системы Хаара эти вопросы исследованы П.Л.Ульяновым [4], [5] и для обобщенной системы Хаара в [6].

При условия принадлежности функции для системы Фабера-Шаудера установила Т.Н.Сабурова [7]. В [8] нами доказана

Лемма 1. Если функции и принадлежат классу , то их произведение принадлежит классу , .

Из леммы 1 вытекает, что класс представляет собой алгебру. Покажем, что в можно ввести норму так, чтобы этот класс стал банаховой алгеброй. Для этого сначала доказана следующая лемма.

Лемма 2. Существует такая константа , что

при любых и , .

Теорема 1. Класс функций , с нормой

(1)

является алгеброй Банаха.

Доказательство. Так как система Фабера-Шаудера является базисом в пространстве , то между функциями и последовательностями их коэффициентов Фабера-Шаудера существует взаимно однозначное соответствие. В частности, это имеет место и для функций класса . Но тогда существует взаимно однозначное соответствие между функциями и последовательностями , где и при . Отсюда и из определения функций класса вытекает, что равенство (1) действительно определяет в классе норму, что класс с этой нормой изометричен полному нормированному пространству последовательностей . Следовательно, класс с нормой, определяемой равенством (1), является пространством Банаха.

Далее, роль единицы в алгебре играет функция . Согласно (1), норма

. (2)

Таким образом, для доказательства теоремы 1 остается показать, что

(3)

при любых . Для этого, прежде всего, заметим, что

(4)

при . Кроме того, так как при , то из леммы 2 следует, что

(5)

при и .

Принимая во внимание (1), (2), (4) и (5) получаем:

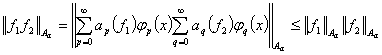
для любых , т.е. справедливо неравенство (3). Таким образом, теорема 1 доказана.

В случае теорему 1 ранее доказала Т.Н.Сабурова [7].

Литература:

1. Кашин Б.С., Саакаян А.А. Ортогональные ряды. – М.: Наука,1984

2. Наймарк М.А., Нормированные кольца, М., ГИТТЛ, 1956.

3. Ульянов П.Л., Об одной алгебре функций и коэффициентах Фурье //ДАН СССР.-1983.-Т.269.-№5.-С.1054-1056.

4. Бари Н.К., Тригонометрические ряды, М., Физматгиз,1961.

5. Ульянов П.Л., Абсолютная сходимость рядов Фурье-Хаара от суперпозиций функций //Anal. Math .-1978.-Т.4.-№3.-С.225-236.

6. Акишев Г.А., Абсолютная сходимость рядов Фурье от суперпозиции функций //Известия высших учебных заведений, Мат.-2009.-№11.-С.3-11.

7. Сабурова Т.Н., Суперпозиции функций и их ряды по системе Фабера-Шаудера, Известия академии наук СССР, Серия математическая.-1972.-Т.36. - С. 401-422.

8. Аменова С.М., Акишев Г., Абсолютная сходимость ряда по системе Фабера-Шаудера суперпозиции функций// Международ.конф. «Дифференциальные уравнения и их приложения»-Актобе-2013.-С.178-180.