Математика / 2.Перспективы информационных систем

Д.т.н. Князьков В.С., аспирант Исупов К.С.

Вятский государственный университет, Россия

Уточненное вычисление приближенной позиционной характеристики чисел в системе остаточных классов

Введение

В последнее время высокопроизводительные вычислительные технологии развиваются необычайно высокими темпами. Причиной этого является появление все новых вычислительных задач, причем требования, предъявляемые этими задачами к методам и средствам их решения, постоянно ужесточаются. Одним из таких требований является необходимость обеспечения высокой вычислительной точности. Многопроцессорная многоядерная архитектура высокопроизводительных систем обуславливает актуальность разработок, направленных на создание методов и алгоритмов, позволяющих выполнять высокоточные вычислительные операции с распараллеливанием до уровня отдельных разрядов операндов. В этой области бесспорными преимуществами обладают методы, основанные на представлении числовых данных в системе остаточных классов (СОК).

1 Представление чисел в системе остаточных классов

Пусть задан ряд натуральных попарно взаимно простых чисел . Тогда для любых целых таких, что существует целое , которое при делении на p_i дает остаток x_i для всех , где (китайская теорема об остатках [1]). Сказанное означает, что существует изоморфизм между кольцом и прямым произведением колец , а арифметические операции над любым числом X в однозначно отражаются на соответствующих операциях с остатками в кольцах соответственно. Зададим далее последовательность чисел таких, что , где , а – мультипликативная инверсия P_i по модулю p_i, которая отвечает решению сравнения 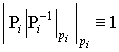. Тогда отображение определится следующим образом

. (1)

Тем самым на основе чисел определяется система остаточных классов (СОК, Residue Number System, RNS) [2, 3] с полным диапазоном P и ортогональными базисами . Число в СОК представляется кортежем , где каждый элемент x_i определяется решением сравнения . Порождающие числа называются основаниями (модулями) СОК. Вычеты x_i в выражении (1) принято называть модулярными разрядами, а образованный их совокупностью кортеж – модулярным числом. Всякое модулярное число в дальнейшем будем обозначать следующим образом:

. (2)

В системе остаточных классов определены основные арифметические операции, которые можно условно поделить на две группы:

1) Модульные операции, к которым относятся: арифметическое (беззнаковое) сложение и вычитание модулярных чисел, умножение модулярных чисел, поразрядное сравнение модулярных чисел и т.д.

2) Немодульные операции, которые включают: сравнение, вычитание модулярных чисел с возможностью получения отрицательного результата, контроль переполнения, округление модулярных чисел (частный случай – масштабирование), деление и т.д.

Важнейшим преимуществом СОК является возможность параллельного выполнения операций по всем модулярным разрядам числа. Например, если и – операнды и необходимо получить результат , такой, что , то функция , отвечающая модульной операции, естественным образом представляется в виде декомпозиции более простых функций таких, что , т.е. каждый разряд результата является функцией разрядов мантисс операндов по соответствующему основанию, и не зависит от остальных разрядов.

Основные недостатки СОК связаны с невозможностью явного определения немодульных операций. В отличие от модульных, немодульные операции требуют знания величины модулярных чисел в целом, а не в остаточном представлении. Иначе говоря, всякая немодульная операция, в данном случае бинарная, суть сложная функция , которая не может быть представлена в виде декомпозиции более простых функций , принимающих в качестве аргументов значения соответствующих модулярных разрядов операндов. Значение каждой цифры результата немодульной операции не является функцией значений соответствующих цифр операндов, а зависит от значений этих операндов в целом.

2 Выполнение немодульных операций в СОК на основе приближенных позиционных характеристик

В основе алгоритмов выполнения немодульных операций лежат методы вычислений позиционных характеристик модулярных чисел [4]. Под позиционной характеристикой принято понимать информацию о позиционном значении модулярного числа (2), т.е. о величине его позиционного эквивалента. Известны точные позиционные характеристики: ранг, след, ядро, коэффициенты обобщенной позиционной системы и т.д. [1–5]. Однако методы их вычисления обладают такими существенными недостатками, как высокая вычислительная сложность и большие аппаратурные затраты на их реализацию [5]. Поэтому полезной альтернативой точных является приближенный метод выполнения немодульных операций, предложенный Червяковым Н.И. и его коллегами в работах [4, 5]. Данный метод основан на вычислении приближенной позиционной характеристики, которая представляет собой округленное значение отношения анализируемого модулярного числа к полному диапазону СОК [4, 5]:

, (3)

Здесь – разряды модулярного числа , – константы, вычисляемые заранее и округленные в пределах разрядности вычислительного устройства, – мультипликативная инверсия от , – дробная часть аргумента. В работе [4] определен ряд простых правил применения приближенных позиционных характеристик для выполнения таких операций, как определение знака модулярного числа, сравнение чисел, обнаружение ошибки и переполнения модулярных чисел и локализации ошибочного разряда.

Главным преимуществом приближенного метода выполнения немодульных операций в СОК является его низкая вычислительная сложность, которая может быть приблизительно оценена как по количеству модулей, в то время как точные методы либо требуют выполнения порядка и более операций, либо вызывают необходимость хранения подстановочных таблиц больших объемов. Например, при известных приближенных характеристиках правило сравнения модулярных чисел и состоит в анализе условий [4]

, , ,

т.е. операция сравнения чисел в СОК сводится к вычислению приближенных позиционных характеристик по формуле (3) и их сопоставлению как обычных дробных чисел, представленных в одном из аппаратно поддерживаемых форматов данных. Вместе с тем, эта же операция при использовании, например, метода потактового перехода к полиадическому коду, требует в предельном случае выполнения тактов, каждый i-ый из которых состоит из операций над модулярными разрядами сравниваемых чисел.

Главный недостаток приближенного метода связан с тем, что вычисление позиционной характеристики по формуле (3) может сопровождаться образованием существенных погрешностей округления, что приводит к некорректному выполнению немодульных операций над модулярными числами. Рассмотрим пример.

Пример. Пусть p₁ = 7, p₂ = 9, p₃ = 11, p₄ = 13 – модули СОК, P = 9009 – их произведение. Для данных модулей константы K_i из формулы (3) определятся следующим образом: , , , . Число разрядов для представления констант выбиралось в соответствии с числом разрядов, необходимых для представления модулей СОК. Пусть , – модулярные числа, которые необходимо сравнить по величине. В соответствии с формулой (3), имеем: , . Таким образом, будет сделан вывод, что . Однако это заключение не соответствует истине. Действительно, преобразуя числа и к целочисленному представлению по формуле (1), получим: , . □

В рассмотренном примере показана ситуация, когда ошибки округления привели к существенной погрешности при вычислении приближенной характеристики модулярного числа : точное ее значение равно , следовательно 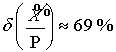. Такое значение погрешности указывает на то, что не содержит ни одного верного значащего разряда, что и привело в итоге к неверному заключению о результате сравнения чисел и . При этом модулярный код числа не указывает явно на возможность появления такой существенной погрешности, вследствие чего верифицировать корректность операции сравнения и , как, впрочем, и любой другой немодульной операции, выполняемой с использованием приближенных позиционных характеристик, не представляется возможным.

Таким образом, актуальной задачей является уменьшение погрешностей округления при вычислении приближенной позиционной характеристики.

4 Способ уточненного вычисления приближенной позиционной характеристики модулярного числа

Получим оценку максимальных погрешностей, которые могут возникнуть при вычислении приближенной позиционной характеристики модулярного числа по формуле (3) с учетом округлений. Пусть в системе остаточных классов с модулями и полным диапазоном задано модулярное число . Пусть – точное значение отношения к P, определяемое, в соответствии с китайской теоремой об остатках, следующим образом:

. (4)

Здесь предполагается, что все слагаемые представленной суммы определяются точно (без округлений). Представим отношение мультипликативной инверсии от P_i к модулю p_i в виде:

,

где K_i – константа СОК из формулы (3), вычисленная с конечной точностью представления, а – ее абсолютная погрешность округления. Тогда, воспользовавшись законами распространения абсолютных ошибок при умножении [6], получим:

.

где – модулярные разряды числа . Так как , то

.

Известно, что максимальная абсолютная погрешность алгебраической суммы приближенных чисел равна сумме абсолютных погрешностей слагаемых, поэтому при суммировании получаем

,

где определяется по формуле (4). Следовательно, если приближенная позиционная характеристика определяется по формуле (3), то ее абсолютная и относительная погрешности будут ограничены сверху неравенствами

, .

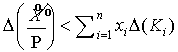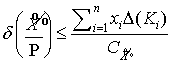Заключаем таким образом, что погрешности, возникающие при определении приближенной позиционной характеристики по известной формуле (3), существенным образом зависят от суммы значений знакопозиций модулярного числа . Пусть двоичное представление констант состоит из k разрядов, причем под дробную часть отведено k – 1 разрядов. Если все модули СОК состоят так же из k разрядов, то при округлении «до ближайшего» . Следовательно,

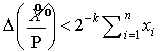, , . (5)

Алгоритмическим способом уменьшения погрешностей (5) является изменение порядка арифметических действий при вычислении приближенной позиционной характеристики с ограниченной точностью по формуле (4): вначале следует вычислить произведение , а уже потом поделить его на соответствующий модуль СОК . Это позволит избежать накопления погрешностей при умножении округленного числа на соответствующий модулярный разряд. Важным является замечание, что целая часть отношения не влияет на значение приближенной позиционной характеристики, вследствие чего произведение можно заключить под знак модуля, что позволит работать исключительно с числами, меньшими, чем . Таким образом, получается следующая уточненная формула для определения приближенной позиционной характеристики модулярного числа:

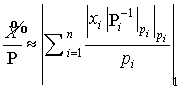. (6)

Погрешность каждого слагаемого в представленной сумме не зависит напрямую от значений знакопозиций и определяется при использовании алгоритма округления «до ближайшего» половиной значения младшего разряда машинного представления вычисляемой позиционной характеристики. Так, если под представление отведено k двоичных разрядов (и столько же для каждого модуля СОК), причем дробной части отвечает разряд, то по закону распространения абсолютных погрешностей при суммировании [6] имеем следующие оценки погрешностей, свойственные формуле (6):

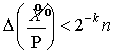, , . (7)

Сопоставив оценки (5) и (7), получим, что формула (6) позволяет уменьшить погрешности в ходе вычисления приближенной позиционной характеристики в раз, где отвечает среднему арифметическому значения i-ой знакопозиции модулярного числа :

.

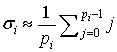Пример. Возьмем исходные данные из рассмотренного ранее примера: , , , , P = 9009. Для представленных модулей СОК значения мультипликативных инверсий определятся следующим образом: , , , . Пусть, как и в предыдущем примере, требуется сравнить модулярные числа и . Вычисляя их приближенные позиционные характеристики в соответствии с (6), с округлением до двух десятичных разрядов после точки, получим:

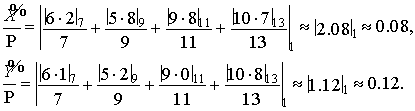
Очевидно, что , поэтому будет сделан верный вывод, что . Таким образом, при равных условиях применение формулы (6), в отличие от формулы (3), позволило получить правильный результат сравнения. □

Заключение

Таким образом, с помощью изменения порядка арифметических действий, удалось существенно уменьшить значения ошибок округления, возникающих при вычислении приближенной позиционной характеристики модулярного числа. Алгоритм уточненного определения приближенной характеристики по формуле (6) требует выполнения n обращений к памяти за выборкой значений мультипликативных инверсий, n умножений, n делений и одну операцию n-операндного суммирования с отбрасыванием целой части. Таким образом, его временная сложность, выраженная в условных тактах, составляет 4n, где n – количество модулей СОК, в то время, как формула (3) требует приблизительно тактов. Порядок сложности при этом остается прежним, .

Литература:

1. Кнут Д. Искусство программирования для ЭВМ. Т. 2. Получисленные алгоритмы. Пер. с англ. – М.: Мир, 1977. – 728 с.

2. Акушский И.Я. Машинная арифметика в остаточных классах / И.Я. Акушский, Д.И. Юдицкий. – М.: Советское радио, 1968. – 440 с.

3. Omondi A. Residue Number Systems theory and Implementation. – London : Imperial College Press, 2007. – 312 p.

4. Приближенный метод выполнения немодульных операций в системе остаточных классов / Червяков Н.И., Авербух В.М., Бабенко М.Г., Ляхов П.А., Гладков А.В., Гапочкин А.В. // Фундаментальные исследования. – 2012. – №6. – С. 189–193.

5. Червяков Н.И. Методы, алгоритмы и техническая реализация основных проблемных операций, выполняемых в системе остаточных классов // Инфокоммуникационные технологии. – 2011. – №4. – С. 4–12.

6. Копченова Н. В. Вычислительная математика в примерах и задачах: Учебное пособие / Н. В. Копченова, И. А. Марон. – Издательство «Лань», 2008. – 368 с.