Умаров А.А., Жумашева Т., Агманова З.

РАЗРАБОТКА ИМИТАЦИОННОЙ МОДЕЛИ ИГРЫ

И АНАЛИЗ ЕЕ РЕШЕНИЙ

Описывается алгоритм имитационной игры преследования и проводится статистический эксперимент. На основе эксперимента определяются оценки оптимальности решений игры. Имитационная модель адекватно отражает процессы преселедования.

Введение. Модели конфликтных ситуации – игровые модели относятся к кибернетическим моделям. Кибернетика (от греческого слова “искусство управления”) – наука, занимающаяся процессами управления в живой и неживой природе, связанными с преобразованием и обработкой информации [2]. Основной объект исследования кибернетики – Кибернетические системы (КС), рассматриваемые абстрактно, вне зависимости от их материальной природы. Примеры кибернетических систем – автоматы, роботы, ЭВМ, человеческий мозг, биологические популяции и многое другое. Каждая такая система представляет собой множество взаимосвязанных элементов, способных воспринимать, запоминать и перерабатывать информацию, а также обмениваться ею.

Сфера применения игровых моделей широка, начиная от простых компьютерных игр до сложнейших биологических и генетических систем

В военное время, в боевых операциях прогнозирование стратегий противника дает возможность угадывания его намерении и предупреждение от внезапных неожиданных атак на уязвимые части, подразделения. В военной энциклопедии [1] приводится такое определение “преследование – вид боевых действий, имеющих целью уничтожения или пленения противника”.

В мирное время стратегии преследования используются в спортивных играх. В популярной игре футбол защитник преследует нападающего, чтобы он не наносил удары в его ворота.

В природе (биологических системах) [2] п р о б л е м а в ы ж и в а н и я особей напрямую связана с данной задачей. Например, от качественного принятия решений убегающего зависит жизнь зайца, где роль преследователя выполняет волк. Эта проблема имеет место во всех уровнях жизни (молекулярном, клеточном и т. д.). Таким образом, любой живой организм борется за свое существование и продолжение жизни методом преследования и убегания.

В настоящей работе описывается модель игры простого преследования с быстродействием для двух игроков – преследователя (игрока П) и убегающего (игрока У) [3, 6].

Разработка модели игры. 1. Постановка задачи.

Настоящая модель игры является: непрерывной (множество стратегий непрерывно и бесконечно); антагонистической (интересы обоих сторон прямо противоположны); динамической (дифференциальной) игрой.

Движение управляемой системы, то есть игороков П и У то задаются выражением (2) – (3).

По особым характеристикам данная игра является [4]:

- игрой с ‘линией жизни’;

- игрой на быстродействие.

Должны быть заданы:

начальные условия игры:

- начальные положения игроков П и У; {P (x₀, y₀), и E (a₀, b₀)}

- начальный момент времени {T₀}

граничные условия игры:

- область преследования; {S}

- часть границы области преследования,

(линия жизни) куда игрок У стремится достичь

до поимки его игроком П {KÎS}

функция платежа:

F^* = d = ® extr, (1)

где F^* является функцией расстояния и для каждого игрока имеет свою цель:

- F^* ® min для игрока П

- F^* ® max для игрока У

Ценой игры n является в р е м я, то есть игрок П должен поймать игрока У (цель) как можно быстрее (оптимальное время преследования), а игрок У должен достичь ЛЖ как можно за короткое время (оптимальное время убегания).

Критерий l – захвата L, который показывает минимальное расстояние между игроком П и игроком У, и от этой величины (F^*£ L) зависит исход игры в пользу игрока П. В нашем случае L = 40.

Отчет очков в игре напрямую связан с показателем времени.

Ограничения игры:

Время t Î [100, 99, … 0]

Область преследования S

Множество S –плоскость, т.е. является функцией S (x,y). где

x Î [10, 580],

y Î [10, 400];

“Линия жизни” К является подмножеством S, то есть KÎS.

Новые местоположения (ходы) игрока П определяются по формулам:

(2)

для игрока У:

где i = 0, 1, … n (3)

Управление игроком У осуществляет человек, который выбирает один из четырех возможных действии по направлениям: ¬,,®,¯.

Исход игры может заканчивается только выигрышем или проигрышем.

В случае поимки игрока У за конечное время получается проигрыш (поражение) и выводится сообщение Ц е л ь у н и ч т о ж е н а!!! В противном случае, когда игроку П удается достичь ЛЖ (убежать) получается выйгрыш и выводится сообщение Ц е л ь н е о б н а р у ж е н а!!!

Игра оценивается показателем времени и выводится в виде очков на экране дисплея.

2. Cтатистический эксперимент. Решение игры осуществляется методом статистических испытаний. Первоначальное исследование модели выполнено в виде 20 испытаний (табл.1)

Таблица 1

Номер эксперимента	Время	Очки	Исход	В
1	51	0	Цель уничтожена (проигрыш)	0
2	100	10	Время истекло (проигрыш)	0
3	28	0	Цель уничтожена (проигрыш)	0
4	19	0	Цель уничтожена (проигрыш)	0
5	76	25	Цель не обнаружена (Выигрыш)	1
6	65	0	Цель уничтожена (проигрыш)	0
7	64	30	Цель не обнаружена (Выигрыш)	1
8	21	0	Цель уничтожена (проигрыш)	0
9	76	25	Цель не обнаружена (Выигрыш)	1
10	87	20	Цель не обнаружена (Выигрыш)	1
11	100	10	Время истекло (проигрыш)	0
12	29	0	Поражение (проигрыш)	0
13	76	25	Цель не обнаружена (Выигрыш)	1
14	100	10	Время истекло (проигрыш)	0
15	81	0	Цель уничтожена (проигрыш)	0
16	64	30	Цель не обнаружена (Выигрыш)	1
17	87	20	Цель не обнаружена (Выигрыш)	1
18	60	0	Цель уничтожена (проигрыш)	0
19	76	25	Цель не обнаружена (Выигрыш)	1
20	87	20	Цель не обнаружена (Выигрыш)	1

Здесь В – булева функция, принимающая значение:

- 0, если исход игры – проигрыш;

- 1, если исход игры – выигрыш;

Ход выполнения эксперимента можно разделить на этапы:

n Выбор оптимальных стратегий;

n Определение самой оптимальной стратегий и ее оценка;

n Определение оптимального времени убегания.

Из таблицы 1 видно, что из 20 испытаний:

- 11 партии игры закончились поражением для игрока У (П р о и г р ы ш);

- 9 партии игры закончились в ы и г р ы ш е м для игрока У.

Так как нас интересуют только выигрышные исходы игры, мы выбираем только 9 результатов (3 стратегий с ценой игры n₁=64, n₂=76 и n₃=87 соответсвенно). Их обозначим через S_64, S₇₆ и S_87. Они являются оптимальными стратегиями убегания. На втором этапе исследования проводим порядка 100 испытаний с выбранными тремя стратегиями S_64, S₇₆ и S₈₇. В таблице 2 приведена частота выигрышей каждой из этих стратегий.

Таблица 2.

x	64	76	87
N	28	39	33

Оптимальная стратегия убегания выбирается исходя из минимизации среднего времени выигрыша игрока У при выбранном объеме испытаний. Статистическая оценка оптимального времени стратегии [5, 6] осуществляется с помощью анализа доверительного интервала математического ожидания. Сначала задаем доверительную вероятность g=0, 95 и в следующем порядке находим:

- математическое ожидание (выборочное среднее измерений):

(4)

-

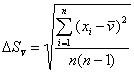
дисперсию (среднеквадратическую погрешость результата измерений):

(5)

- ошибку серий измерений:

(6)

- доверительный интервал (ошибку серий измерений):

(7)

где t – коэффициент Стьюдента, зависящий от числа измерений n, g - вероятность того, что истинное значение измеряемой величины n лежит в доверительном интервале (7).

Найденные оценки измерений:

(8)

Отсюда можно утверждать, что средний выигрыш (ожидаемый) равен 76, 27 (математическому ожиданию). И он лежит в интервале (8).

Стратегию S₇₆ (оптимальную стратегию убегания), которая обеспечивает средний выигрыш, обозначим через v₀. Момент времени, максимально обеспечивающий достижение ЛЖ игроку У (о п т и м а л ь н о е в р е м я у б е г а н и я), обозначим через T_j.

Проведенные в данном случае двадцать испытаний недостаточны для полной оценки ситуаций. Качественная оценка достигается при большом числе опытов, поряка (N>500). Но, исходя из известного Закона больших чисел можно сделать следующий вывод:

С заданной вероятностью (g=0, 95) стратегия v₀ является оптимальным в игре преследования для игрока У в том случае, когда игрок П использует стратегию непрерывного преследования u₀. С той же вероятностью можно утверждать, что оптимальное время убегания T_j лежит в доверительном интервале (8).

3. Составление программы имитационной игры. Программа игры была названа Preslej. Ее название берется от слова «преследование». Сложность алгоритма - средний. Трудности встречаются при реализации игры:

n при определении используемых параметров (скорости игроков П и У);

n при разделении глобальных переменных от локальных;

n при несоответствии типов при вводе параметров;

В процессе реализации программы Preslej были сделаны 8 версии (модификации). С каждой новой версией были внедрены новые возможности, улучшения. Программа Preslej используется в учебном процессе ВУЗа по предмету Математическое моделирование [6].

Список литературы

1. Военная энциклопедия СССР – т.2, – М.: Просвещение, 1977

2. Кузин Л. Т. Основы кибернетики. В двух томах. Математические основы кибернетики – М.: Энергия, 1973 –474с.

3. Петросян Л. А., Томский Г. В. Интеллектуальные Игры Преследования –Новосибирск: Наука, 1991-125с.

4. Петросян Л.А., Зенкевич Н.А., Семина Е.А. Теория игр: учеб. пособие для ун-тов. – М.: Высш. шк., 1998. – 304 с. ил.

5. Апанасов П. Т. , Орлов М. И. Сборник задач по математической статистике - Уч. пособие для вузов, М.: Высш. шк., 1987- 303с.

6. Умаров А.А. О создании программы Preslej - Труды Межд. научно- методической конференции “Инновационное обучение физ., мат., информатике: актуальные вопросы и перспективы” МКТУ ШИ, 2004, с.415-417.