Математика/4. Прикладная математика

К.т.н. Димитриев А.П.

Чувашский государственный университет имени И.Н. Ульянова, Россия

Раскрашенные Сети Петри и задача размещения

Составление расписания учебных занятий является задачей размещения непрерывных учебных пар в течение недели. В его математической модели учебные занятия представим n непрерывными объектами разной длительности p_i, i=1, …, n, значения t_i и начала в течение периода. Период состоит из m моментов времени [1]. Цель размещения – минимизация функционала

,

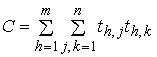где t_h,j – значение t_j в h-й момент периода, равное либо t_j, либо нулю, что зависит от p_j и начального момента размещения объекта.

Пусть m=10 и даны объекты, которые надо разместить (табл. 1):

Таблица 1.

Заданные объекты

Имя объекта	A	B	C	D	E	F	G	H
ti	5	2	4	2	3	10 (0Аh)	7	3
pi	2	3	7	8	5	4	5	6

Разработана программа для получения близкого к оптимальному размещения. С ее помощью получено размещение на рис. 1, а) где С=943.

АААА000000 (F) 0000333333 (H) 0000777770 (G) 0004444444 (C) 5000000005 (A) 0222000000 (B) 3330000033 (E) 0222222220 (D) а)

2222222200 (D) 0000000055 (A) 5555500000 (G) 0000033333 (E) 4444440004 (C) 0000002220 (B) 3333300003 (H) 00000AAAA0 (F) б)

AAAA000000 (F) 0000777770 (G) 3333000003 (E) 0000333333 (H) 2200000002 (B) 0022222222 (D) 0444444400 (C) 0000000055 (A) в)

Рис. 1. Различные размещения

Применение сетей Петри в задаче составления расписания исследовано в [1]. В дополнение разработана модель на раскрашенных сетях Петри, объединяющая объекты в кластеры, чтобы затем манипулировать меньшей размерностью входных данных и таким образом уменьшить временную сложность алгоритма (рис. 2).

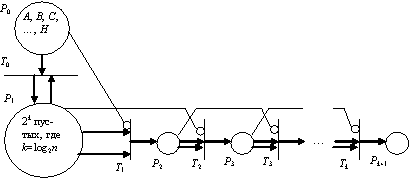
Рис. 2. Модель, объединяющая кластеры (многоуровневые)

Размещение, получаемое моделью рис. 2, изображено на рис. 1, б), здесь четыре кластера первого уровня: DA, GE, CB, HF объединены в два кластера второго уровня: DAGE, CBHF; С=997, что отнюдь не идеально. Это можно объяснить тем, что, в отличие от одиночных объектов, кластеры имеют уже внутри себя некоторое слагаемое для С.

На рис. 2 переход Т₀ производит заполнение пустых маркеров в Р₁. На входе сети набор маркеров А, В, С, …, Н, их количество не должно быть больше 2^k. Переходы Т_i, i=1,…,k объединяют два маркера в один, причем приоритет делается для двух непустых маркеров, затем для пустого с непустым, и только затем для двух пустых. Для объединения выбираются маркеры с наибольшей и наименьшей суммами р. Выходной маркер – результат объединения, помещается в Р_i+1. Он создается с таким взаимным расположением содержимого двух входных маркеров, чтобы было наименьшее С внутри полученного набора (структура входных маркеров не нарушается, меняется только из взаиморасположение). Итоговое размещение будет в P_k+1.

Разработана также модель на сетях Петри без объединения кластеров первого уровня в более высокоуровневые (рис. 3).

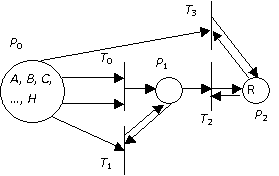
Рис. 3. Модель без объединения кластеров

Здесь переход Т₃ имеет низкий приоритет. В Р₂ находится сначала пустое размещение, которое затем обновляется при срабатывании Т₂ или Т₃. Переход Т₀ объединяет два маркера из Р₀ в один. Для объединения маркеры берутся так, чтобы отклонение по t не превышало 2, либо общая длина не превышала m более, чем на 2. Если после помещения в Р₁ у маркера до m суммы длин не хватает, срабатывает Т₁ (тоже если сумма не станет больше m+2), у него высокий приоритет. У Т₃ низкий приоритет, он срабатывает , если остался один маркер в Р₀. Переходы Т₁ и Т₀ просто ставят два объекта один после другого. T₃ и Т₂ ставят в размещение новые кластеры или объект туда, где лучше всего (не нарушая структуры кластера). Размещение, получаемое моделью рис. 3, изображено на рис. 1, в), здесь четыре кластера: FG, EH, BD, CA; С=948.

Таким образом, получаемое значение С больше, чем без использования кластеров. Особенно это проявляется в многоуровневой модели кластеров.

Литература:

1. Желтов В.П., Димитриев А.П. Стохастическая оптимизация расписания на сетях Петри. Чебоксары, Изд-во Чуваш. ун-та, 2001. 213 с.