Кесиян Г.А., д.ф.-м.н. Уртенов. М.Х.

Кубанский государственный университет, Россия

Стохастическая модель финансового инструмента, учитывающая взаимосвязь цены, объема и открытого интереса

При принятии инвестиционных решений на фондовом рынке трейдеры часто используют данные по объемам торгов. Объем определяется как количество купленных или проданных единиц инструмента за определенный промежуток времени. Этот показатель характеризует активность на рынке и его большие значения зачастую подтверждает устойчивость трендов.

При рассмотрении стратегий, связанных со среднесрочной и долгосрочной торговлей, у инвесторов появляется возможность использовать данные не только по ценам и объемам, но и данные по открытому интересу (open interest). Открытый интерес – это количество нереализованных контрактов за определенный промежуток времени [2]. Это индикатор степени ликвидности рынка.

Когда объем и открытый интерес находятся на низком уровне, то торговать в такой ситуации стоит очень осторожно (неликвидный рынок). Это связано с тем, что высоколиквидные рынки менее всего подвержены манипулированию со стороны трейдеров.

Несмотря на то, что большинство инвесторов сходятся во мнении, что объем и открытый интерес являются факторами второстепенными, помогающими подтверждать сигналы технических индикаторов, значимостью этих факторов пренебречь нельзя.

Учитывая вышесказанное, мы предлагаем класс стохастических моделей, которые предполагают взаимосвязь цены X, объема V и открытого интереса I некоторого финансового инструмента. Данный класс моделей можно представить следующей системой стохастических дифференциальных уравнений (СДУ):

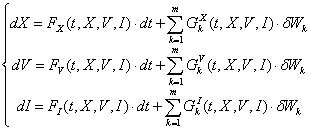, ₍₁₎

_{где δW – это бесконечно малый винеровский «шум».}

_{В общем виде m не обязательно равно количеству уравнений в системе, то есть не обязательно, что m=3.}

Условная плотность распределения вероятностей состояния системы (1) является решением уравнения Фоккера — Планка (второе уравнение Колмогорова):

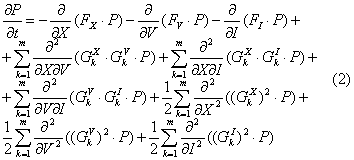
В данном уравнении аргументы функций опущены для простоты записи. Имея условную плотность распределения вероятностей, можно вычислять среднее, волатильность, автокорреляционную функцию и другие характеристика случайного процесса.

Для решения уравнения (2) используется начальное условие в виде 3-мерной дельта - функции Дирака, равной произведению одномерных функций по каждой координате [3]:

,

где x вектор:

.

Уравнение Фоккера — Планка (УФК) является параболическим дифференциальным уравнением в частных производных второго порядка, и для его решения, кроме начального условия, необходимы также граничные условия на концах интервала изменения x. Граничные условия могут иметь различный вид [1, 3]:

- отражающие граничные условия изменяют знак приращения dx при достижении границы;

- поглощающие граничные условия предполагают прекращение процесса при достижении границы;

- периодические граничные условия накладывают, когда при достижении некоторой границы x=a происходит перемещение x на другую границу x=b, откуда процесс продолжает развиваться в соответствии со стохастическим уравнением.

Литература:

1. Гардинер К.В. Стохастические методы в естественных науках. М.: Мир, 1986.

2. Мэрфи Д.Д. Технический анализ фьючерсных рынков: теория и практика.- М.: Сокол, 1996. -592с.

3. Степанов С.С. [Электронный ресурс] // Стохастический мир : электрон. версия книги / Сергей С. Степанов. – [Б.м.], 2011. – С. 224-227. - URL: http://synset.com/pdf/ito.pdf.