ФИЗИКА/ 2.Физика твердого тела.

Захарченко Р.В.^1,2, Захарченко В.Н.¹

¹Національний технічний університет України «КПІ», Україна

²Лабораторія дослідження матеріалів при Національному політехнічному інституті Мексики, відділення Керетаро, Мексика

Дослідження оптичних процесів в наноструктурному пористому кремнії

В даній роботі наведено результати дослідження оптичних процесів в наноструктурному кремнії, розглянуті спектри збудження та випромінювання, вплив магнітного поля на фотолюмінесценцію.

Наявність сильної видимої люмінесценції в ниткоподібних кремнієвих наноструктурах (найчастіше їх називають пористим кремнієм або por-Si) привертає до себе велику увагу, оскільки очевидна несумісність із зонною структурою нормального кремнію та завдяки багатьом потенціальним застосуванням пористого кремнію в оптоелектроніці. Найбільш популярні пояснення такого випромінювання базуються на квантовому розмірному ефекті [1], хоча існує і багато інших моделей [2-11], все ще потребуючих доведення своєї адекватності.

Нещодавно було впроваджене нове наближення (Торчинська [5,12]), в якому процес збудження люмінесценції представляється як балістичний ефект (балістичне транспортування фотоелектронів до межі розподілу Si/SiO_x), спричинений гарячими електронами, які створюються оптичним поглинанням в Si нанокристалітах з практично незмінною зонною структурою, та гарячими електронами зони провідності також приймаючими участь в процесі.

Ціллю даної роботи було дослідити динамічні характеристики електронів, що приймають участь в збудженні фотолюмінесценції. Нами були отримані нові експериментальні результати, які підтверджують останнє наближення, а також дана оцінка середньої рухомості електронів (що збуджують випромінювання), з якої випливає, що збуджуючі випромінювання електрони є гарячими електронами.

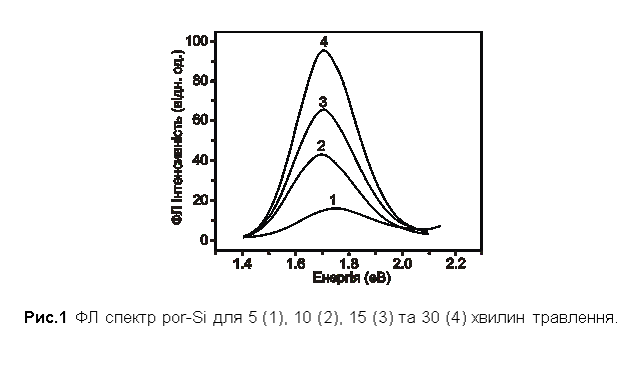
На рис. 1 зображені ФЛ спектри зразків por-Si з різним часом травлення; очевидно, що всі три спектри мають практично однакову форму без будь-якої залежності від характеристичного розміру деталей наноструктури (форма кривих майже однакова для усіх умов травлення). На рис. 1 крива 1 ФЛ спектру відповідає зразкам з 5-ти хвилинним травленням; крива 2 – зразок з 10-ти хвилинним травленням, криві 3 та 4 – зразки з 15-ти та 30-ти хвилинним травленням відповідно. AFM зображення поверхні кремнію після 15-ти хвилинного травлення, представлене на рис. 2, показує деталі поверхні кремнію пірамідальної форми з розміром 40 – 80 нм, які забезпечують ([12,13]) оптимальну інтенсивність фотолюмінесценції (ФЛ). Морфологія поверхні por-Si змінюється в залежності від тривалості травлення: середній розмір Si нанокристалітів зменшується від 150 нм (5-ти хвилинне травлення) до 40 – 80 нм (при 15 – 30 хвилинній обробці поверхні).

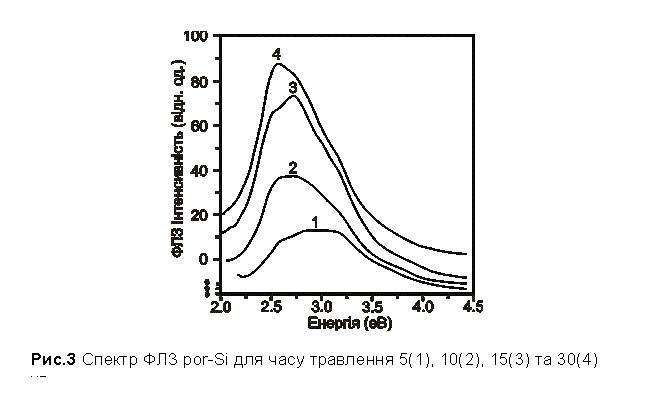
На рис. 3 представлено спектр збудження фотолюмінесценції (ФЛЗ) для зразків por-Si, виготовлених при густині струму анодування величиною 20 мА/см² з повною тривалістю травлення в 5 (крива 1), 10 (2), 15 (3) та 30 (4) хвилин. Як видно з рисунку, його приблизно можна описати як суперпозицію трьох широких зон, центрованих відповідно при 2.55, 2.82 та 3.2 еВ. На відміну від спектру випромінювання, його форма змінюється в залежності від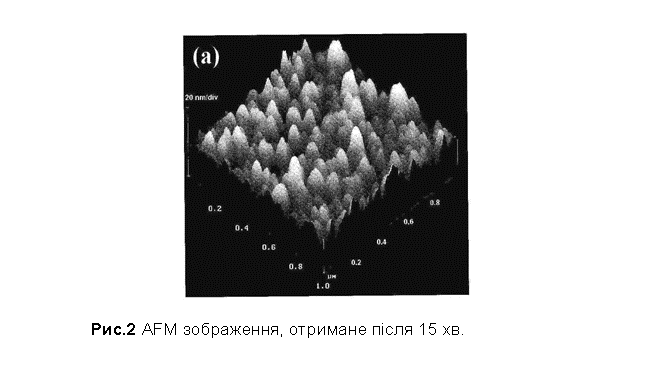
характеристичних розмірів структури por-Si. Із збільшенням часу травлення (та відповідним зменшенням розміру поверхневих Si нанокристалітів) відносна частина низькоенергетичних складових спектру збудження фотолюмінесценції збільшується. Це збільшення (зображене на рис. 4) показує зміну ефективності збудження ФЛ в трьох вище згаданих спектральних регіонах із збільшенням часу травлення зразка (тобто із зменшенням розміру структурних деталей).

Поведінка ефективності збудження в перших двох регіонах майже однакова і дає збільшення приблизно в три рази, тоді як в третьому регіоні, що відповідає найвищій енергії збудження, це збільшення набагато менше.

Наведені дані вже показують, що квантоворозмірні ефекти не відповідають за емісію, що спостерігається: для характеристичного розміру розглядуваної поверхні (див. рис. 2) ці ефекти не досконало розроблені (приймаючи до уваги, що деталі більш меншого розміру, які дійсно можуть забезпечити квантоворозмірні ефекти, швидко окислюються, то ми їх з цієї причини і не розглядаємо). З іншого боку, для цих ефектів залежність форми спектру від характеристичного розміру повинна буди дуже сильною, чого у нашому випадку немає (рис. 1).

Напроти, балістична модель, запропонована в [12,13], добре погоджується із стабільним емісійним спектром, який, з позицій цієї моделі, визначається радіаційними дефектами на межі розподілу Si/SiO_x. Збудження цих дефектів забезпечується гарячими електронами, які генеруються індукованими світлом переходами з валентної зони Si до його зони провідності [12,13].

Вплив магнітного поля на фотолюмінесценцію. Продовжуючи тему балістичної моделі, слід очікувати, що магнітне поле буде впливати на інтенсивність емісії, оскільки електрони з високою енергією (“гарячі”) мають

порівняно високу швидкість, і тому магнітне поле повинно мати помітний вплив на їх рух, зменшуючи їх середню довжину вільного пробігу і тим самим, відповідно, зменшуючи їх можливість досягти тих місць межі розподілу де знаходяться радіаційні центри. На рис. 5 зображено відносне зменшення інтенсивності емісії, спричинене магнітним полем. До Si зразка ми прикладали магнітне поле величиною 0,52 Тл таким чином, що напрямок магнітного поля був паралельний до поверхні зразка (тобто нормальний до осей “нанопірамід”, сформованих травленням, див. рис. 2). Люмінесценцію збуджували за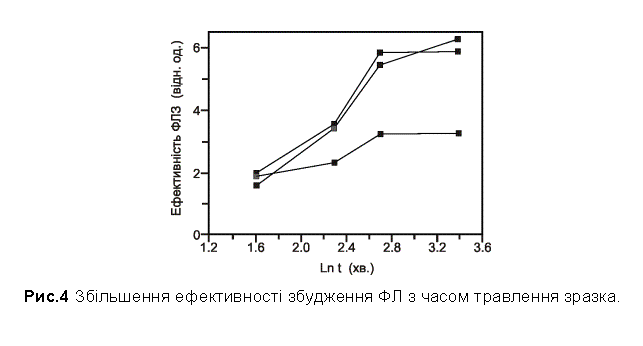
допомогою ртутної дугової лампи; емісія в різних спектральних інтервалах була підібрана за допомогою монохроматора (МДР-4); інтенсивність емісії вимірювали за допомогою фотоелектропомножувача. З рис. 5 видно, що зменшення інтенсивності люмінесценції не залежить від довжини хвилі емісії і дорівнює 10% від початкового значення інтенсивності (кажучи іншими словами, ФЛ інтенсивність з прикладеним магнітним полем дорівнює 0,9 початкового значення ФЛ інтенсивності в даному спектральному регіоні).

Трактування отриманих результатів на основі квантової та балістичної моделей. По-перше, ми повинні відзначити, що спектр випромінювання, який ми спостерігали в наших експериментах, не залежить від характеристичного розміру структури, а в спектрі збудження фотолюмінесценції (ФЛЗ) така залежність існує. Це, звісно, вказує на те, що електронні переходи, відповідальні за випромінювання, не пов’язані з квантовими енергетичними рівнями в Si нанокристалітах por-Si (хоча, повністю виключати присутність квантово-розмірних ефектів в збудженні не слід), а, найбільш імовірно, визначаються радіаційними дефектами поблизу межі розподілу Si/SiO_x, пов’язаними з окисленням. Отже, порівняємо дві моделі збудження фотолюмінесценції – першу, що використовує квантові ефекти із збудженням переходів між квантово-розмірними локалізованими станами та – другу, яка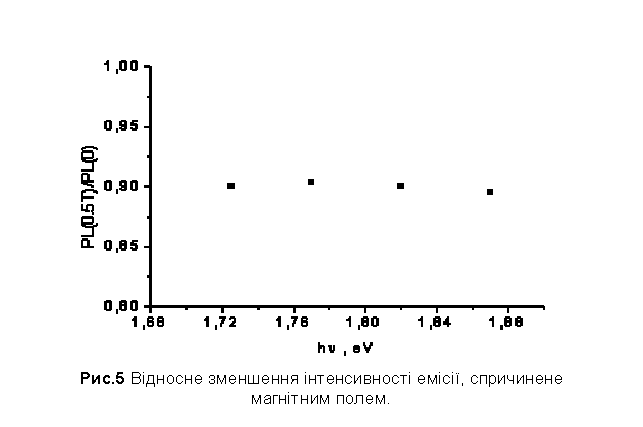
застосовує квазібалістичний вільний рух гарячих електронів в незмінній енергетичній зоні з наступним збудженням оксидних дефектів поблизу межі розподілу Si/SiO_x.

Модель збудження, пов’язана з квантово-розмірними ефектами. З AFM зображення (рис. 2) ми можемо бачити, що верхня частина усіх деталей поверхні por-Si структури може бути приблизно розглянута як напівсфери з діаметром приблизно 5 нм, що може, в принципі, забезпечити систему квантових рівнів, підходящих для електронного збудження з наступною рекомбінацією всередині Si нанокристалітів або тунелювання до поверхневого дефекту (тобто до поверхневих центрів випромінювання) електронів з енергією високою у порівнянні з енергією рівноважних електронів в об’ємному Si. Електрони в згаданих квантових станах можуть бути представлені стоячими хвилями де-Бройля, сформованими багатократними відбиваннями від стінок квантової ями (поверхня зразка або, точніше, межа розподілу Si/SiO_x). Якщо ця межа розподілу містить радіаційний центр, існує певна імовірність захвату електрона на цей центр з наступним випромінюванням ФЛ фотона. Ця модель, хоча можлива і може бути корисною для деяких випадків, не може пояснити відносне зменшення інтенсивності випромінювання під впливом магнітного поля. У випадку квантово-розмірних систем, можливий вплив магнітного поля на випромінювання може мати форму ефекту Зеємана, який (і) вимагає великих полів, щоб добре проявлятись, та (іі) торкається, перш за все, спектру випромінювання, і в меншому ступені інтенсивності випромінювання. Однак, ми спостерігаємо досить помітний вплив на інтенсивність, обумовлений порівняно невеликим магнітним полем, та не маємо залежності впливу від довжини хвилі випромінювання.

Балістична модель збудження. Відповідно до цієї моделі (деталі в [19, 26]), спектр збудження формується поглинанням світла в Si з нормальною (подібною до об’ємного кремнію) енергетичною зонною структурою внаслідок непрямих оптичних переходів (в основну долину /точку мінімуму/ зони провідності поблизу точки Δ₁, та, відраховуючись від енергії фотона в приблизно 1.6 еВ, до іншого екстремуму поблизу точки L₁) та внаслідок прямих переходів до вищої центральної Г₁₅ – Г₂₅ або L₁ – L₃ мінімуму при приблизно 3.2 – 3.4 еВ, та Х₄ – Х₁ при 4.25 – 4.50 еВ.

Інтенсивність збудження фотолюмінесценції І_PLE для спектрального регіону з низьким поглинанням та для тонких зразків (αd<1) можна представити як

де R – коефіцієнт відбиття,

α – коефіцієнт поглинання,

η – квантова ефективність ФЛ,

S – площа поверхні.

Якщо R та η не змінюються під впливом збуджуючої світлової енергії в досліджуваному спектральному регіоні, то інтенсивність збудження ФЛ буде прямо пропорційна до коефіцієнта поглинання для непрямих оптичних переходів:

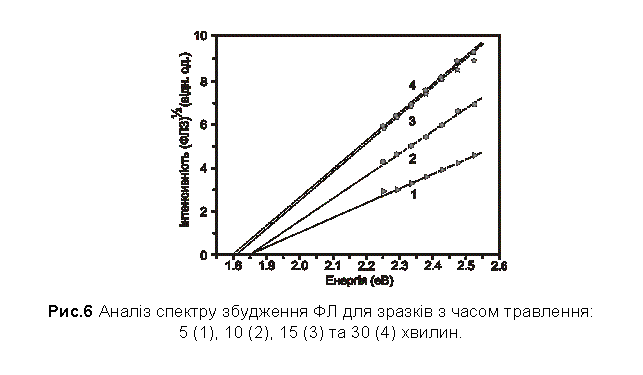
де Е₀ – це сума енергії збудження ФЛЕ_exc для радіаційних оксидних дефектів та енергії деякої кількості фононів, що випромінюються за час оптичних переходів, пов’язаних з поглинанням, в Si нанокристалітах та час квазібалістичного руху фотоносіїв в межі розподілу Si/SiO_x. Як видно з рис. 6, спектр збудження ФЛ в спектральному діапазоні 2.2 – 2.8 еВ задовольняє згадану вище енергетичну залежність. Таким чином, збудження ФЛ в спектральному регіоні 2.2 – 2.8 еВ – це дійсно процес, що протікає за підтримки фононів внаслідок непрямих оптичних переходів в Si нанокристалітах.

Суттєво, що реалізація квазібалістичного транспортування гарячого носія повинна впливати на форму спектру збудження ФЛ в Si нанокристалітах [14]. Фактично, в великих кристалітах (150 нм), в основному, високоенергетичні носії (енергія збудження 2.6 – 3.4 еВ) є ефективними в збудженні ФЛ (рис. 3, крива 1). Останнє є результатом часткової енергетичної релаксації гарячих носіїв з емісією оптичних фононів до досягнення межі розподілу. Із зменшенням розміру нанокристаліта до 40 – 80 нм, навіть менш енергійні гарячі носії (енергія збудження 2.2 - 2.8 еВ) будуть спроможні досягти межі розподілу з енергією, достатньою для участі в збудженні ФЛ. Як видно з Рис. 3 (криві 3, 4) та Рис. 4, інтенсивність збудження ФЛ для por-Si шару з кристалітами розміром 40 – 80 нм, в основному, зростає в спектральному діапазоні 2.2 - 2.8 еВ. В цьому випадку червона межа Е₀ спектра збудження ФЛ для найменших нанокристалітів може зсуватись в низько-енергетичний регіон (мала кількість випромінених фононів), як це видно з Рис. 6 (криві 3 та 4). Таким чином, модифікація форми спектру збудження ФЛ та зсув його червоної межі Е₀ в сторону низьких енергій із зменшенням діаметру Si кристаліта підтверджує роль балістичного ефекту в збудженні “червоної” зони ФЛ.

В основі цієї моделі вплив магнітного поля на інтенсивність випромінювання є очікуваним, оскільки електрони високих енергій (“гарячі”) мають порівняно високі швидкості, і прикладене до зразка магнітне поле повинно було б мати помітний вплив на рух цих електронів, зменшуючи їх середню довжину вільного пробігу L. Це зменшення довжини вільного пробігу обумовлене дією сили Лоренца, яка збільшує час польоту електрона до поверхні і, відповідно, зменшує кількість гарячих електронів, що спроможні збудити видиму ФЛ. Ця кількість, в припущенні, що час релаксації та швидкість залишаються сталими, зменшується з часом t (х - відстань польоту) внаслідок процесів розсіяння по закону:

де n₀ – це початкова кількість гарячих електронів і τ – час релаксації.

Інтенсивність ФЛ пропорційна значенню n, яка дає кількість електронів, що спроможні досягти межу розподілу без розсіяння. В магнітному полі, “х” необхідно було б замінити більшою дистанцією х^* (час t – замінити на час t^*, х^*/х = t^*/t), яку ми розрахували нижче.

Ми припускаємо, для спрощення, що “x” в виразі (3) – це найкоротша відстань від поверхні, що проходить гарячий електрон, яка супроводжується випромінюванням, та “t” – відповідний час польоту електрона. В магнітному полі електрон рухається вздовж колової траєкторії; за проміжок часу t, електрон пройде частину траєкторії, що визначається кутом j обертання радіусу R цієї траєкторії за цей проміжок часу t. Таким чином, збільшений шлях подорожі буде рівним . Значення кута j визначається циклотронною частотою , де “e” – це заряд електрона, а “m” – його ефективна маса. Кут j дорівнює , (де – це рухомість електронів). Виконуючи деякі відповідні геометричні розрахунки ми отримуємо для рівняння (3) (для гарячих електронів досягаючих поверхні в магнітному полі) наступний вигляд

Для малих кутів ми можемо розкласти останню експоненту в ряд і врахувати лише перші дві складові, що з врахуванням формули для j дає нам вираз залежності інтенсивності ФЛ від магнітного поля

Як правило, час польоту більше за час релаксації. Візьмемо, для грубої оцінки, значення приблизно рівним 1 (тобто ), з експериментально отриманого 10% впливу магнітного поля на інтенсивність ФЛ ми отримуємо Це дає значення рухомості Таке значення рухомості набагато перевищує нормальну рухомість електронів в кремнії (), і, таким чином, визначально вказує на наявність ефекту гарячих електронів. Час релаксації, розрахований з цього значення рухомості, з використанням усередненого значення ефективної маси, як це зазвичай роблять для описання явищ переносу, де m_l та m_t – це поздовжня та поперечна електронні маси відповідно, буде , що добре погоджується з попередніми оцінками [14]. Для швидкості гарячих електронів [14], це дає середню довжину вільного пробігу в 90 нм, що приблизно відповідає розміру нанокристалітів в приповерхневому шарі por-Si. Відзначимо, що зміна розміру нанокристаліта з 150 нм до 40 – 80 нм в різних зразках por-Si призводить до зміни червоної межі їх спектра збудження ФЛ з Е₀ = 1.86 еВ (для кривих 1, 2) до Е₀ = 1.80 еВ (для кривих 3, 4) (див. Рис. 6), різниця енергій в 60 меВ дуже близька за значенням до енергії оптичного фонона в об’ємному Si.

Пористий кремній як «просвітляюче покриття». На рис. 7 представлені дані вимірювань по відбиванню світла від шару por-Si, нанесеного на c-Si. Верхній спектр (квадрати) відноситься до дзеркального відбиття при нормальному падінні світла; дзеркальне відбивання під іншими кутами падіння не дуже відрізняється і має той самий порядок величини (приблизно 7,5%). Слід нагадати, що відбиття видимого світла від поверхні чистого с-Si має величину порядку 35% із-за великого значення показника заломлення матеріалу (варіюється від 5,5 при 400 нм до 3,75 при 700 нм). Рис. 7 ясно показує, що пористі шари діють як гарне антирефлекторне покриття. Нижня крива (кола) це інтенсивність експериментально виміряного розсіяного світла при куті 60^o; її залежність від довжини хвилі приблизно наближається до закону (трикутники на графіку) типового для Релеївського розсіювання, яке доводить її природу. Інтенсивність розсіяного світла, проінтегрована по усім кутам розсіяння та усереднена по досліджуваній спектральній області дає приблизно 1% від падаючої інтенсивності, що не дає великого внеску до втрат на відбивання, зображених верхньою кривою.

Такий шар пористого кремнію (por-Si) може бути змодельованим в його взаємодії з електромагнітними хвилями як гомогенна плівка з його реальною товщиною (20 – 60 нм), що має усереднений по товщині шару показник заломлення з наступних міркувань: (а) електромагнітна хвиля проникає крізь відбиваючий матеріал на відстань порівняну із довжиною хвилі, яка значно більша ніж товщина шару, (б) класичне відбивання пропорційне до , де це різниця в показниках заломлення прилеглих шарів, отож відбивання між різними частинами (por-Si) шару розділене невеличкою відстанню , яка пропорційна до і тому є нехтовно малою. Таким чином, ми вважаємо, що світло відбивається por-Si шаром з товщиною “L” та середнім показником заломлення n^*, оточеним з одного боку вакуумом (n = 1), і з іншого – с-Si . Ми приймаємо, що деталі поверхні в шарі пористого кремнію (рис. 2) мають оптичні властивості об’ємного Si [12 ], тож залежність n(x) в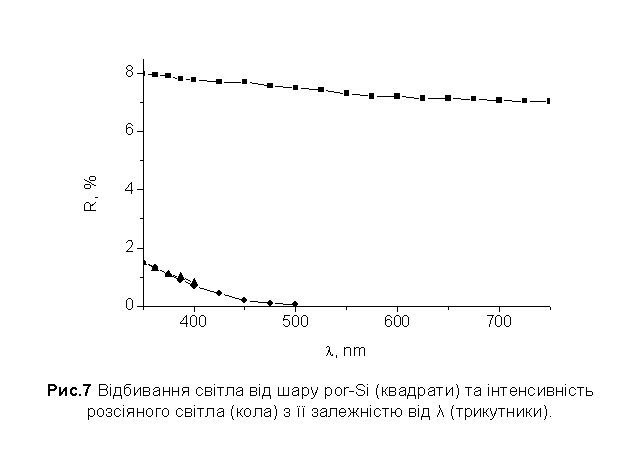
шарі por-Si обумовлена геометрією цих деталей поверхні (колони, нитки, піраміди і т.д.). Щоб отримати значення n^*, ми використали два наближення: (1) товщина стовбчастих деталей (r) зростає лінійно з відстанню “x” від зовнішньої поверхні шару, тож “n” буде зростати з “x” по квадратичному закону; і (2) r пропорційна квадратному кореню з “x”, отож “n” має лінійну залежність від координати. Отже

і середнє значення показника заломлення буде

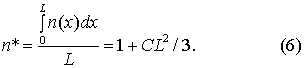
Середнє значення показника заломлення буде

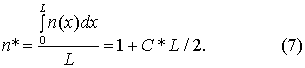
Показник заломлення на зовнішній поверхні шару буде

Беручи для товщини шару por-Si значення L = 30 нм, ми отримуємо для випадку (1) значення n* = 1.98, і для випадку (2) n* = 2.47, що дає для коефіцієнта відбиття R значення в 11% та 18% відповідно. Ці значення приблизно погоджуються з втратами на відбивання, які спостерігались в експерименті, а спектральна залежність відбивання може бути, в першому наближенні, віднесена до спектральної залежності n_o.

Висновки. Спостерігався вплив магнітного поля величиною 0,5 Тл на фотолюмінесценцію нанониток Si: інтенсивність люмінесценції в магнітному полі складала 90% від інтенсивності за відсутності поля. Ефект не має залежності від довжини хвилі емісії. Цей ефект не можна пояснити на базі квантоворозмірної моделі, і підтримується гіпотеза про збудження люмінесценції гарячими електронами, переведеними світлом з валентної зони до вищих рівнів зони провідності Si, в той час як зонна структура спостерігавшихся нанониток Si майже така сама як для об’ємного Si. Із величини впливу магнітного поля ми оцінили ефективну рухомість електронів, приймаючих участь в процесі емісійного збудження, як величину рівну 6000 см²/(В·с). Це значення є значно вищим аніж стандартна рухомість електронів в Si, що також підтримує ідею про балістичний механізм збудження ФЛ за допомогою збудження поверхневих емісійних центрів гарячими електронами.

Проведений аналіз оптичних властивостей шару пористого кремнію показав, що такий шар може бути використаний як «просвітляюче покриття» для сонячних елементів. Представлені результати показують, що класичне наближення до оптичних матеріалів як високо гомогенних, може правомірно бути взятим під сумнів на базі досягнень та ідей нанотехнології, яка дає можливості адаптувати подібний матеріал до специфічних потреб та застосувань.

Література:

1. C. Sanchez, M. In, Molecular Design of Alkoxide Precursor for the Synthesis of Hybrid Organic-Inorganic Gels, J. Non-Cryst. Solids 147/148 (1992), pp. 1-12.

2. A.N. Murashkevich, V.G. Vashina, I.M. Zharskii, Synthesis of Active Porous Silica Gel Materials and Investigation of Their Properties, J. Sol-Gel Sci. and Techn. 20 (2001), pp. 7-12.

3. Griffits, J., Color and Constitution of Organic Molecules, London: Academic, 1976, pp. 24–29.

4. Birks, J.B., Photophysics of Aromatic Molecules, London:Interscience, 1970, pp. 1–26.

5. J.N. Murray, The Theory of the Electronic Spectra of Organic Molecules. John Wile & Sons, Inc., New York, 1963.

6. A.K. Bharava, H.P. Garg, R.K. Argaval, Energy Convers. Manage. 31 (1991) 471-479.

7. Y. Tripanagnostopolus, Th. Nousia, M. Souliotis, P. Yanoulis, Sol. Energy 72 (2002) 217-234.

8. H.A. Zondag, D.W. De Vries, W.G. Van Helden, et al., Sol. Energy 72 (2002) 113-128.

9. J. González-Hernández, J.F. Pérez-Robles, A. Manzano-Ramirez, et al., Appl. Phys. Lett. 75 (1999) 3192-3194.

10. D.R. Lide (Ed.), Handbook of Chemistry and Physics, 80^th ed., 1999-2000, CRC Press, Boca Raton, London.

11. T.V. Torchinska, Optoelectron. Rev. 6 (2) (1998) 121-130.

12. A. Biedermann, O. Genser, W. Hebenstreit et al., Scanning Tunneling Spectroscopy of One-Dimensional Surface States on a Metal Surface, Phys. Rev. Lett., 76 (1996), pp. 4179-4182.

13. M. Schmid, S. Crampin, P. Varga, STM and STS of Bulk Electron Scattering by Subsurface Objects, J. Electron Spectr. And Rel. Phenomena, 109 (2000), pp. 71-84.

14. J.M. Lavine, S.P. Sawan, Y.T. Shieh, and A.J. Bellezza, Appl. Phys. Lett 62, 1099 (1993).