Минарбеков Ж.И.

Таразский государственный университет им. М.Х. Дулати

ДЛИНА СОВЕРШЕННОГО ГИДРАВЛИЧЕСКОГО ПРЫЖКА. ЗАКОН АБДУРАМАНОВА

Проектирование многих гидротехнических сооружений требует знания длины совершенного гидравлического прыжка в нижнем бьефе, ибо от этого параметра потока зависит выбор конструкции сооружений и экономические вопросы строительства. Определению длины совершенного гидравлического прыжка посвящены работы таких ученых как: Н.Н. Павловский, М.Д. Чертоусов, О.М. Айвазян, К. Сафранец, Б.А. Бахметев, А.Е. Матцке, В.А. Шаумян и других [1]. Однако все эти работы носят эмпирически и полуэмпирический характер. Проблема долгое время не поддавалась теоретическому обобщению.

Как известно в 1999 г. А. Абдурамановым получено основное уравнение совершенного гидравлического прыжка из теоремы Эйлера в виде [2].

(1)

где: - расход; – коэффициенты Кориолиса, соответственно для первого и второго сопряженных глубин;

, - площади живого сечения в сопряженных глубинах;

, - половина глубины воды в сопряженных сечениях; ==

- глубина воды в сопряженных сечениях; - осредненная площадь поперечного сечения прыжка; - осредненных смоченный периметр прыжка;

- длина гидравлического прыжка;

- уклон дна русла;

- коэффициент Шези.

Имея в виду, что

=,

из уравнения (1) длина совершенного гидравлического прыжа

(2)

где - прыжковые функции в сечениях, соответствующих сопряженным глубинам;

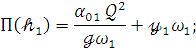
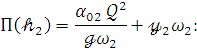
Обозначив - через написанием (2) в виде [2]:

. (3)

Формула (3) выражает закон Абдураманова, который гласит:

длина совершенного гидравлического прыжка прямо пропорциональна разности прыжковых функции в сопряженных глубинах и обратно пропорциональна произведению средных еличин к площади живого сечения и разности к уклонов трения и дна русла прыжка.

Рассмотрим частные случай этого Закона.

1.Если гидравлический прыжок имеет место над горизонтальной плоскостью (і=0), то закон Абдураманова выражается еще короче

. (4)

то есть длина совершенного гидравлического прыжка прямо пропорциональна разности прыжковых функции в сопряженных глубинах и обратно пропорциональна произведению средних величин площади живого сечения и уклона трения прыжка.

2.Если гидравлический прыжок образуется на участке с обратным уклоном русла (-і), то этот Закон пишется в виде

, (5)

и читается так: длина совершенного гидравлического прыжка прямо пропорциональна разности прыжковых функции в сопряженных глубинах и обратно пропорциональна произведению средних величин площади живого сечения и суммы уклонов трения и дна русла прыжка.

В работе [4] показано сравнение вычисленных значений длины гидравлического прыжка по известным формулам выше приведенных ученых с экспериментальными данными. Наиболее близкие результаты к опытным значениям длины гидравлического прыжка дает формула Абдураманова (3).

Литература

1. Әбдіраманов Ә. Гидравлика – Тараз “Сенім” 2010. – 471 б.

2. Абдураманов А. Об основном уравнении совершенного гидравлического прыжка – Механика и моделирование процессов технологии. – Тараз, 1999, № 2. – с. 134-137.

3. Абдураманов А. Некоторые вопросы теории совершенного гидравлического прыжка – Механика и моделирование прцессов технологии. – Тараз, 2000, № 2. – с. 130-135.

4. Джолдасов С.К., Койшыбаева Г.Д. Определение экспериментальным путем длины совершенного гидравлического прыжка.-Материалы международной научно-практической конференций “Уркумбаевские чтения” “Водные ресурсы и пути их рационального использования в современных условях”. - Тараз, 2012. - С.86-89.